ПРИЛОЖЕНИЕ 2
Расчёт величины, именуемой импульсом стационарных полей, для точечного заряда и точечного магнитного диполя
Формулы даны в Гауссовой системе единиц
измерения.
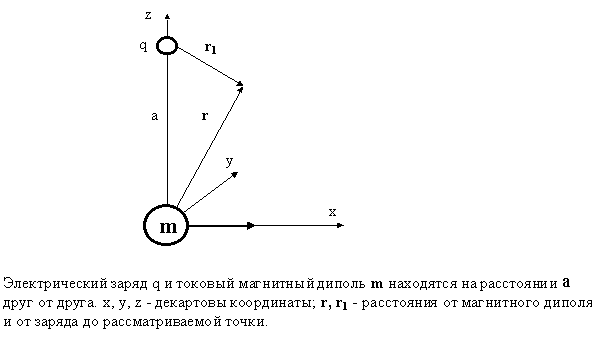
Электрический заряд q (см. рис) находится на расстоянии а по оси z от токового магнитного диполя с магнитным моментом
m, направленным, вдоль оси х. В качестве токового магнитного диполя возьмём равномерно намагниченный шар радиуса R, из непроводящего магнитного материала, относительную диэлектрическую проницаемость которого примем за 1 или вращающуюся вокруг оси х сферу, поверхность которой равномерно заряжена. Размеры частиц будем считать малыми по сравнению с расстоянием между ними. Найти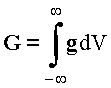
, где 
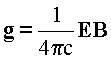, dV =dxdydz,
( G - импульсный потенциал).
82
Сначала будем интегрировать по внешней, по отношению к намагниченной сфере области, затем по внутренней, после чего просуммируем результаты.
Равномерно намагниченный шар в наружной области (r > R) создаёт магнитное поле, эквивалентное точечному диполю с магнитным моментом 
. В области R < r , магнитное поле однородно и равно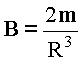 
Решение в области r > R:
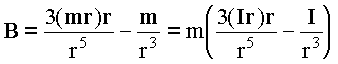, где I - единичный вектор вдоль направления m. Учитывая, что 
; 
, получим: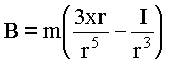 
.
Так как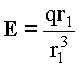 
, где 
- расстояние, отсчитываемое от заряда, то
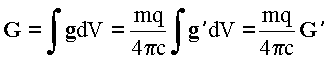, где 
, 
- напряжённость электрического поля единичного заряда, - магнитная индукция магнитного диполя с единичным магнитным моментом.
Распишем и 
по компонентам:
; 
; 
;
; 
; 
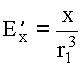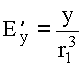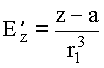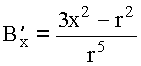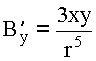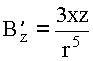
Так как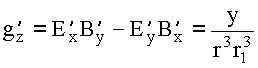 
нечётно по
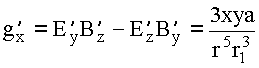нечётно по x, y, то 
и 
.
83
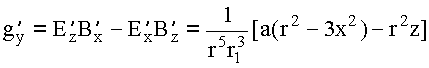
Переходим к сферическим координатам:
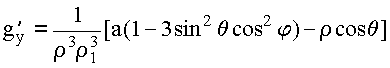
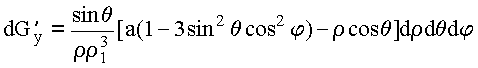
Делаем замену переменных: 
Обозначим: 
, где 
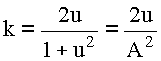
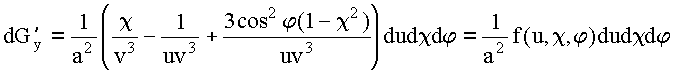
84
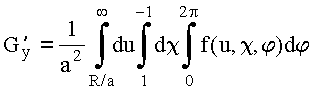
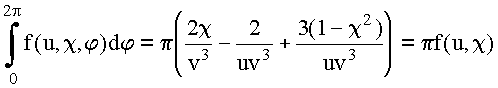
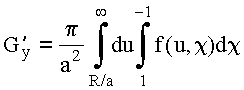
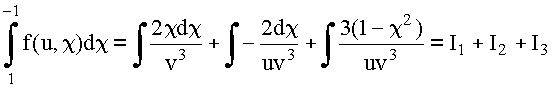
Обозначим: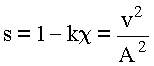 
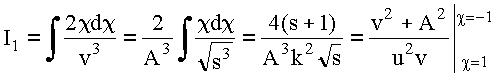
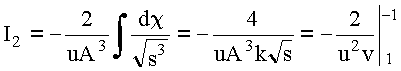
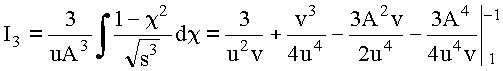
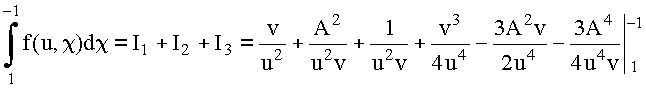
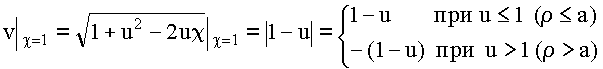
Ищем решение в области 
85
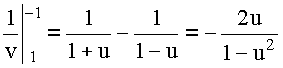
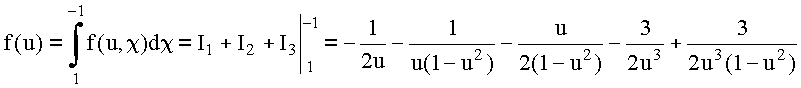
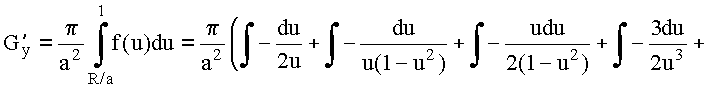
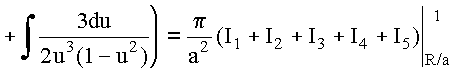
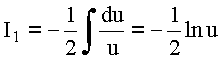
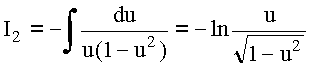
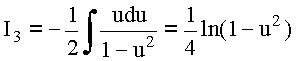
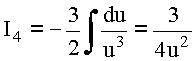
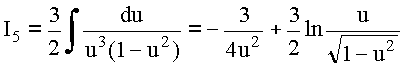
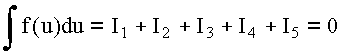
86
Таким образом, в области 
.
Ищем решение в области 
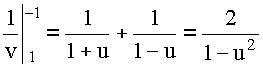
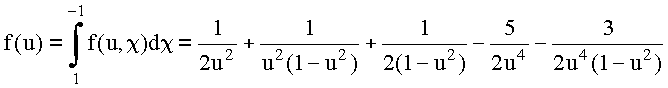
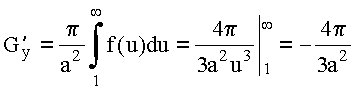
Так как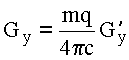 
, то результат для внешней, по отношению к сфере области имеет вид: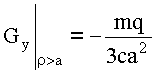 
Перейдём теперь к внутренней области сферы 
. Так как по условию 
, то электрическое поле внутри сферы можно считать постоянным.
Очевидно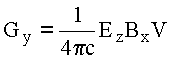 
, где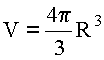 
- объём сферы. Подставляя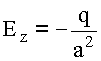 
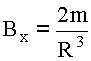, получим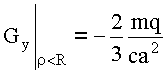 
Следует отметить, что полученный результат остаётся справедливым, даже если радиус сферы не является малым , по сравнению с расстоянием от центра сферы до заряда.
Складывая результаты для внутренней и внешней областей получим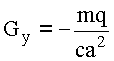 
87
Выпишем все компоненты вектора 
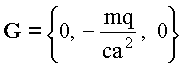, Учитывая, что при продольной ориентации магнитного диполя (а не поперечной как в рассмотренном случае) =0, можно записать: 
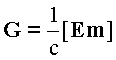, где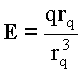 
- напряжённость электрического поля, создаваемого зарядом в точке нахождения магнитного диполя, 
- расстояние, отсчитываемое от заряда.
Полученная формула справедлива для обоих вариантов магнитного диполя, оговоренных в условии задачи т.е. шар из равномерно намагниченного непроводящего магнитного материала (
=1) или непроводящая равномерно заряженная вращающаяся сфера т. к. индукции магнитных полей в обоих случаях одинаковы. Мало того, результат вообще не зависит от формы магнита, т. к. любой объём можно представить в виде суммы сферических составляющих (главное чтобы выполнялось условие малости размеров элементов по сравнению с расстоянием между ними).
Формула для
G путём интегрирования допускает распространение на системы, содержащие так же и протяжённые заряженные и магнитные элементы. Например,фактор
G для намагниченной пластины малой толщины, объёмом V, по величине будет равным G = EMV/c2 , где M - величина вектора намагниченности, направленного вдоль длины или ширины пластины, Е - величина электрического поля внутри пластины, направленного вдоль её толщины. В частном случае, если магнитный элемент состоит из проводящего материала или окружён проводящей оболочкой, то G = 0, т. к. внутри такого магнита E = 0. Полученный путём прямых вычислений результат 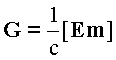противоречит мнению авторов ряда работ (см. И.Е.Тамм. Основы теории электричества. Издательство технико-теоретической литературы, М.,”НАУКА”, 1989, с. 404 ; Фейнман, Лейтон, Сэндс. Фейнмановские лекции по физике, т.6, изд-во “Мир”, 1977, стр. 59, 304; Физическая энциклопедия под ред. А. М. Прохорова, М., 1998, т.2 , с.131), основанном не на подобных вычислениях,
88
а на общих соображениях, в связи с
чем концепция импульса и энергии (вектор Пойнтинга) стационарных электромагнитных полей становится беспочвенной, а результаты эффектов, связанных с такими полями имеют иное объяснение (см. настоящий сайт).89
Размещено на сайте 12.02.2016.
Статьи других авторов
На главную
