Власов В.Н
Подведение итогов моделирования маятника
Бесслера,
а также колёс Бесслера и Альдо Коста.
Продолжаем моделирование гравитационных колёс и маятников в программе «Живая физика». Несмотря на некоторые ограничения, заложенные в этой программе, удалось получить интересные результаты с далеко идущими выводами. В этой статье будет сделана попытка обобщить итоги моделирования гравитационных колёс Бесслера и Альдо Коста, а также маятника Бесслера. Колёса Бесслера и Альдо Коста – это общеизвестный факт. И поэтому сам по себе механизм моделирования в программе «Живая физика» подтверждает, что такие колеса имеют полное право на признание в качестве, если не вечного двигателя, то двигателя гравитационного, в котором раскрутка колеса осуществляется в первую очередь за счет параметрического резонанса. Что касается того, был ли у Бесслера его маятник именно параметрическим, сейчас сказать трудно, но то, что конструкция маятника Бесслера позволяет из него сделать параметрический маятник, это уже проверенный в программе «Живая физика» факт.
Самое главное, обнаружено, что изменяться положение груза, как в маятнике, так и в колесе, должно совершенно не так, как предполагали многие конструкторы «вечных» двигателей. Правда моделирование строилось на предположение, что грузы можно перемещать с помощью электромагнитов и фиксировать их в нужной позиции с помощью защелок. Но даже это позволяет теперь приступить к конструированию таких колёс с полным пониманием того, что мы хотим от таких гравитационных двигателей и как они должны работать. Останется только разработать сам механизм перемещения груза в нужное время и нужном месте, чтобы затраты энергии при этом были небольшими и не отнимали всей энергии у работающего колеса или маятника.
Поэтому было решено повторить некоторые модели, а заодно попробовать проверить путём моделирования все идеи, которые, так или иначе, появились в процессе моделирования машин Бесслера и Альдо Коста.
В качестве параметра был выбран самый простой – массы грузов, которые могли изменяться в зависимости от положения их относительно горизонтальной или вертикальной оси, проходящей через ось колеса или маятника. А после проведения моделирования будем предполагать, что изменением массы груза мы изменяли момент инерции этого груза и получали таким образом реакцию колеса в виде ускорения, либо замедления их угловой скорости, или увеличения амплитуды и частоты колебаний для маятников.
Изменять момент инерции грузов можно за счет смещения их вдоль радиуса колеса или поперечной планки маятника. Или за счет разделения или слияния их масс с одновременным перемещением частей вдоль радиуса колеса или поперечной планки маятника. А для разделения и слияния масс можно использовать электромагниты, электростатику, гидросистему или придумать подходящую механическую систему. Решил же эту задачу Бесслер, чем современные инженеры и врачи хуже.
Моделирование начнем с маятника Бесслера, у которого на поперечной планке параметрически изменяется масса одного груза (рис.1) по закону if(Body[6].p.y>0,Input[28], Input[29]). Input[28] – это значение самого верхнего регулятора, а Input[29] - это значение второго сверху регулятора, т.е., максимальная и минимальная масса синего груза.
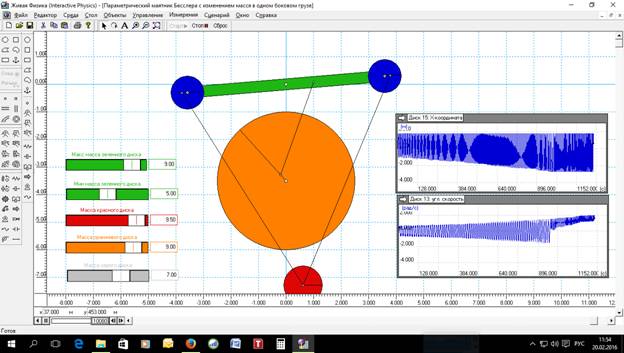
Рис.1 Результат
моделирования маятника Бесслера,
в котором изменяется масса только одного левого синего груза.
На рис. 1 приведены результаты моделирования. Масса левого зеленого груза может изменяться импульсно с 5 кг, когда груз находится ниже горизонтали, проходящей через ось маятника, до 9 кг, когда груз находится выше этой горизонтали. Масса красного груза составляет 9.5 кг, серого груза, который запускает колебания маятника, - 7 кг, оранжевого колеса (маховика) – 9.5 кг. Для изменения перечисленных параметров, в первую очередь левого зеленного груза, используются горизонтальные регуляторы, показания которых можно видеть на рис.1. В правой части рисунка имеются два индикатора, на которых фиксируются: на верхнем – амплитуда горизонтальных колебаний красного груза, а на нижнем – угловая скорость оранжевого колеса (маховика).
Прекрасно видно, что после запуска процесса амплитуда колебаний красного груза и угловая скорость оранжевого колеса нарастает по закону, близкому к гармоническому. Правда «синусоида» сильно искажена, колебания явно нелинейные. Примерно на 900 секунде амплитуда колебаний красного груза стабилизируется, а колесо начинает уже совершать обороты на 360о, постепенно набирая угловую скорость (частоту). Если просмотреть оба графика, то можно заметить, что для параметрических колебаний этого маятника характерно то, что частота колебаний стабильно нарастает от начала процесса. Видно, что на промоделированном интервале времени частота колебаний далека от стабилизации. А это указывает на то, что такая система будет со временем набирать мощность именно за счет увеличения частоты колебаний. Есть ли у такой системы предел? Да, как показывают моделирование с большей массой для красного груза, при повышении этой массы обязательно наступает момент, когда амплитуда и частота колебаний маятника стабилизируются. Так что, скорее всего, Бесслер использовал в своих колесах маятники именно для ограничений частоты вращения и мощности колеса. Без такого ограничителя для колеса пришлось бы разрабатывать ограничитель другой конструкции. Бесслер выбрал хорошо известный ему маятник специальной конструкции, в котором можно легко менять грузы на необходимые для выбранной мощности колеса.
Теперь усложним модель. Пусть теперь масса обеих синих грузов изменяется параметрически по выбранному закону (рис.2). Формула остается той же самой, только в каждой формуле подставляется номер соответствующего тела.
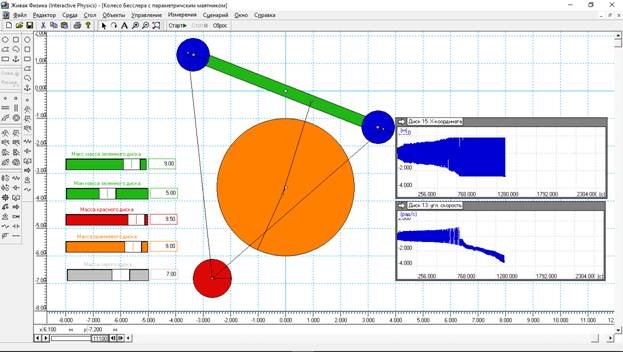
Рис.2 Результат
моделирования маятника Бесслера,
в котором изменяется масса обоих синих грузов.
Значения на регуляторах такие же, как и на рис.1. А вот уже на индикаторах мы видим уже что-то другое. Главное, что вращаться оранжевое колесо начинает через 700 с. А через 1200 с колесо выходит на угловую частоту в два раза больше, чем в первом варианте. Так что можно утверждать, что использование в маятнике двух грузов, масса которых параметрически меняется, приводит к удвоению мощности на оси маховика. Естественно, если у оранжевого маховика будет установлено 2 таких маятника, то мощность увеличится уже в 4 раза.
С параметрическими маятниками, имеющими форму, близкую к тому, что использовал Бесслер в своей машине, можно сказать, мы разобрались. И если теперь думать о практическом использовании полученных результатов, то любой, у кого руки растут из положенного места, а голова находится между ушами, смогут самостоятельно изготовить энергетическую установку, для которой не надо никакого топлива. Главное, правильно выбрать материалы, подобрать массу грузов, правильно сконструировать маховик, к которому придется подключать электрогенератор, скорее всего, через редуктор. Но самое главное – выбрать вариант изменения моментов инерции грузов на концах поперечной планки маятника. И помнить, что если груз поднимается выше горизонтальной линии, проходящей через ось маятника, то момент инерции этого конца перекладины должен быть максимальным, а если груз находится ниже горизонтальной линии, то момент инерции опущенного конца перекладины должен быть минимальным. Само же изменение момента инерции синих грузов, с большего на меньший и обратно, должно происходить тогда, когда поперечная планка будет находиться в горизонтальном положении.
Между прочим, в ножной швейной машинке этот принцип используется давно. Ведь в неё педаль – это поперечная перекладина, а колесо связано с педалью именно так, как на рис. 1 или 2. Единственно, что нет красного груза. А вот момент инерции меняется так, как в проанализированных моделях. Ведь швея давит на педаль либо пальцами, либо пяткой ноги, что равноценно изменению массы и момента инерции концов педали. Так что опытная швея тратит на поддержание мощности маховика меньше энергии, чем выдает маховик уже в саму машинку.
Считаю, что с маятниками всё понятно. И что для энергогенератора надо использовать именно маятник Бесслера, так как в таком маятнике изменение массы грузов на горизонтальной планке можно производить параллельно поверхности Земли, практически не затрачивая при этом энергии, особенно, если в такую систему встроить рекуператоры энергии. Правда у такой конструкции есть одно слабое место, нельзя заранее определить в какую сторону будет вращаться маховик. Поэтому такая система нуждается в таком запуске, чтобы оранжевый маховик сразу же начал вращаться в одну и нужную сторону. А набор угловой скорости – это уже дело наживное, само пойдет.
Теперь начнем моделирование колес. Самое простое колесо – это горизонтальная планка с грузами на концах с осью посередине – детские качели. Уже на этой конструкции можно получить все важнейшие результаты. Поэтому возьмем для начала уже изученную модель маятника, уберем из неё маховик и нижний груз (рис.3). Формулы у обоих синих грузов для изменения массы остается без изменения, те же, что в колесе Беслера.
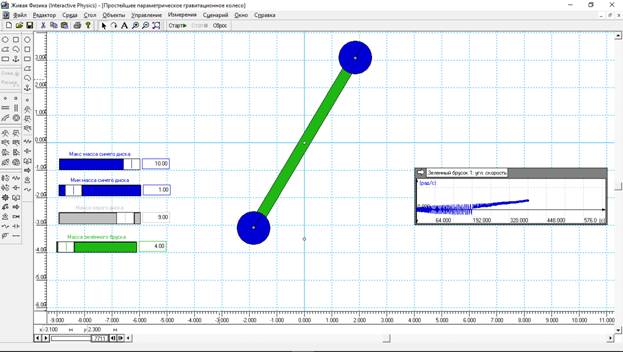
Рис.3. Результат моделирования колеса Бесслера из двух грузов.
На рисунке показан результат в момент остановки моделирования на 380 с. Длина между центрами синих грузов примерно 7 м. Масса зеленного бруска 4 кг. Масса серого груза для инициации процесса 9 кг. Максимальная масса синего груза, когда он находится в верхней полуплоскости – 10 кг, а минимальная масса синего шара, когда он находится в нижней полуплоскости – 1 кг. Конструкция вначале колебалась вокруг горизонтальной линии, а потом через 195 с колесо из двух грузов начало вращаться против часовой стрелки. Частота вращения такого колеса линейно нарастала с 196 с по 380 с. Но радует то, что неравномерность угловой скорости такого колеса по мере роста частоты вращения уменьшается.
Для интереса я попробовал задать для зелённого бруска массу в 200 кг. Результат моделирования оказался таким. После инициации примерно 170 с колесо раскачивалось, на 170 с немного покрутилось против часовой стрелки, затем снова примерно 20 с вновь начала колебаться, потом в течении 40 с два раза изменила направление вращения, пока на 250 с колесо не начало устойчиво вращаться по часовой стрелке, медленно увеличивая частоту вращения. Так что для устойчивого вращения надо подбирать оптимальное соотношение между длинной зеленного бруска, его массой, минимальной и максимальной массой синих грузов. Это уже дело будущего.
Теперь заставим промоделировать нашу пару грузов колесо Альдо Коста. Теперь формула для одного груза будет выглядеть так - if(Body[6].p.х>0,Input[28], input[29]), где Body[6].p.х – это X‑координата для центра тяжести груза (тела) [6]. Для другого груза формула аналогичная, только там задаются свой номер груза (тела). Результат моделирования показан на рис.4.
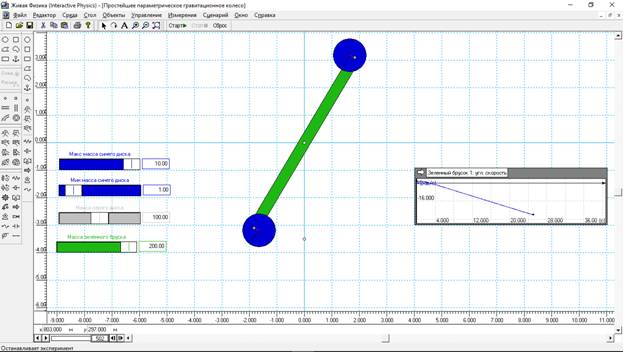
Рис.4 Результат моделирования простейшего колеса Альдо Коста.
Параметры зеленного бруска и синих грузов такие же, как в предыдущем варианте. А вот масса серого груза выбрана в 200 кг. Можно было серый груз не использовать, так как колесо с самого начала неуравновешенно. Результат моделирования показан на индикаторе справа. Видно, что за несколько секунд колесо набирает значительно более высокую частоту, совершив только в первую секунду одно колебание, далее только линейный набор частоты. Причем в момент остановки моделирования начала деформироваться связь между бруском и синими грузами. Скорее всего через несколько секунд колесо бы развалилось на части.
Результаты моделирования показывают, что колесо Альдо Коста, скорее всего, будет обладать большей энергией или лучше поддерживает своё вращение. Но с другой стороны это может означать меньшую устойчивость в ответ на действия случайных факторов. Колесо, которое будет нагружено на электрогенератор должно держать стабильную мощность и частоту вращения, а не «бросаться» из стороны в сторону, грозя развалиться при первой же неприятности. Встроить отрицательную обратную связь, чтобы не допускать разрушительных частот вращения, думаю, не составит особого труда.
Теперь перейдем уже к моделированию «настоящих» колёс. Для начала попытаемся смоделировать колесо Бесслера, для которого примем, что масса грузов изменяется в момент пересечения груза горизонтальной линии, проходящей через центр ось колеса (рис.5).
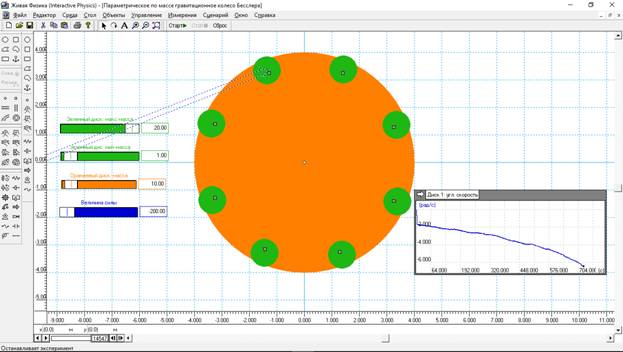
Рис.5. Результат моделирования колеса Бесслера с 8 грузами.
Колесо (оранжевый диск) диаметром 8 метров. Восемь грузов (зеленные диски) масса которых определяется регуляторами зеленного цвета. Верхний регулятор задает массу груза, когда груз находится в верхней половине диска, а второй – массу, когда груз находится в нижней половине диска. В данном случае максимальная масса равна 20 кг, а минимальная 1 кг. Столь большая разница может вызвать массу вопросов, типа, что и как. Но мы решаем задачу в предположении, что управляем моментом инерции грузов, поэтому для нас сейчас важен качественный результат. Оранжевый регулятор задает массу оранжевого диска, она равна 10 кг. Пунктиром показана сила, которая прикладывалась к одному из грузов в первые 5 с в целях начальной раскрутки колеса. Сила эта «привязана» к грузу и изменяла свое направление вместе с изменением положения груза. В течение 5 секунд величина этой силы, первоначально направленной вниз, была равна -200 н.
В правой части рисунка находится индикатор, показывающий угловую скорость оранжевого диска (колеса). Колесо вращается по часовой стрелке. Видно, что в период раскрутки угловая скорость колеса увеличилась с 0 до 2 рад/с, а затем уже колесо само наращивала угловую скорость и на 700 с значение угловой скорости было уже 6 рад/с. По форме кривая роста угловой скорости напоминает параболу. Эксперимент прерван, так как удалось четко выявить поведение колеса - после запуска оно при заданном управлении моментом инерции вращается, увеличивая угловую скорость.
Формула, по которой изменялись массы зеленных грузов выглядит так:
if(Body[X].p.y>0,Input[38],Input[39]) (1)
где X – это номер зеленного диска (груза), который задается программой самостоятельно.
Input[38] – это значение максимальной массы, снимаемое с регулятора 38.
Input[39] – это значение минимальной массы, снимаемое с регулятора 39.
Body[X].p.y – это Y- координата диска с номером Х.
Теперь изменим во всех грузах формулу для массы на следующую, чтобы получить вместо колеса Бесслера колесо Альдо Коста:
if(Body[X].p.x>0,Input[38],Input[39]) (2)
где Body[X].p.x – это Х - координата диска с номером Х.
Внешний вид экрана (рис.6) изменится незначительно, все данные те же, что в предыдущем эксперименте, за исключением величины силы, которая равна нулю, так как колесо тяжелее справа (со стороны экспериментатора).
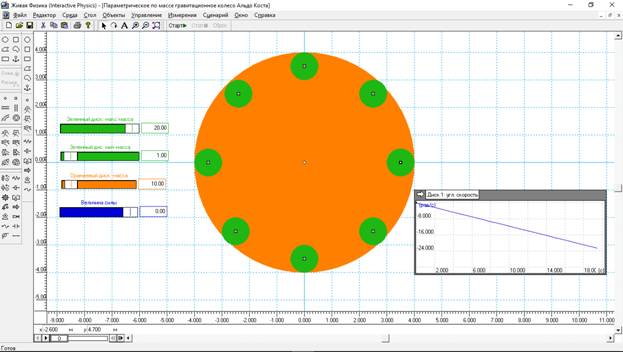
Рис.6. Моделирование колеса Альдо Коста.
Индикатор справа показывает, что после запуска колесо Альдо Коста сразу же начинает по линейному закону набирать огромную частоту вращения. За 20 с угловая скорость составила 20 рад/с. Это примерно 3 оборота в секунду. Что для колеса с диаметром в 8 м довольно много. При дальнейшем увеличении угловой скорости происходит разрушение колеса, поэтому пришлось ограничиться временем регистрации в 20 с.
Осталось еще провести моделирование так, чтобы посмотреть, как будут вести себя системы, где маятник Бесслера будет объединён с колесом Бесслера или Альдо Коста. Но думаю, что в этом нет никакой необходимости. Главная работа сделана. На простых примерах показано, что маятники будут сами качаться, а колеса сами вращаться, если в маятники или колеса встроить механизм перемещения грузов, чтобы реализовывался именно промоделированный вариант изменения момента инерции грузов, что приводит, как ни странно, именно к раскрутке колеса и раскачки маятника. Правило очень простое, как для колеса Бесслера, которое можно запускать в как по часовой стрелке, так и против.
|
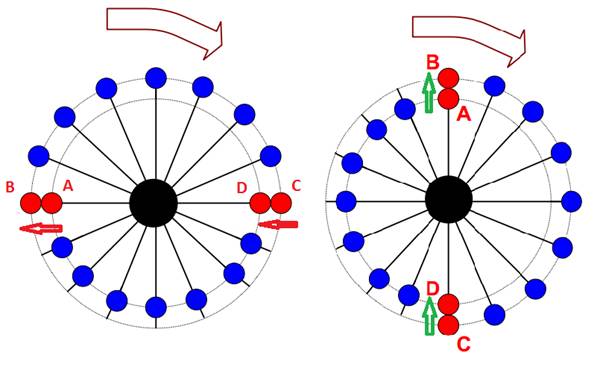
Перемещение грузов в колесе Бесслера. |
Перемещение грузов в колесе Альдо Коста. |
Рис.7.
На рис. 7 слева показано, как должно изменяться положение грузов в колесе Бесслера. В точке, где груз переходит из нижней полуплоскости в верхнюю, груз надо смещать с внутренней орбиты на внешнюю., то есть из положения A в положение B. А когда груз переходит из верхней полуплоскости в нижнюю, то груз должен смещаться с внешней орбиты на внутреннюю, то есть из положения C в положение D. Если делать обратное, то колесо вращаться не будет, а уже вращающееся колесо постепенно остановится.
На том же рис.7. справа показано, как должно изменяться положение грузов в колесе Альдо Коста. Тут уже вращение возможно только в одну сторону. И когда груз подходит к нижней точке колеса, то есть в момент перехода из правой полуплоскости в левую он должен быть поднять на некую высоту, переведен с внешней орбиты на внутреннюю. Если груз подходит к верхней точке колеса, в момент перехода из левой полуплоскости в правую, он опять должен поднят на некую высоту. А в системе координат, связанной с вращающимся колесом он должен сместиться с внутренней орбиты на внешнюю.
Теперь осталось промоделировать вращение колеса с нечётным числом грузов. Выберем вариант колеса Бесслера с тремя грузами. Можно с одним, но это уже будет высшим пилотажем, некоторый, особенно некоторые академики, просто не поймут и начнут бубнить о лженауке. Возьмем уже готовые модели колеса Альдо Коста или Бесслера, и по окружности через 120 градусов установим всего три груза. Вначале изучим поведение колеса Альдо Коста (рис.8).
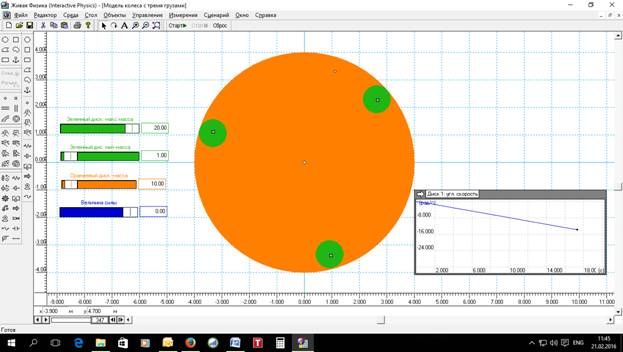
Рис.8. Модель колеса Альдо Коста с тремя грузами.
У данной модели колеса Альдо Коста три груза, масса которых изменяется по формуле, которая была показана выше. Максимальная масса каждого зеленного груза 20 кг, минимальная – 1 кг, оранжевого диска 10 кг, а значение силы 0 н. Для запуска колеса Альдо Коста использовать дополнительную силу нет необходимости – работает смещенный вправо центр тяжести колеса. Индикатор справа показывает рост угловой скорости колеса – на 17 секунде угловая скорость приблизилась к 12 рад/с. Эксперимент показал, что колесо Альдо Коста может успешно крутиться с нечетным числом грузов. Теперь составим модель колеса Бесслера с тремя грузами. Сделать это легко, достаточно немного подправить формулу каждого груза – рис.9.
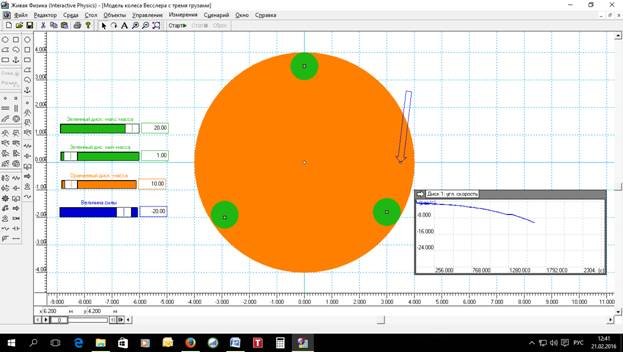
Рис.9. Модель колеса Бесслера с тремя грузами.
Максимальная масса каждого зеленного груза – 20 кг, минимальная масса – 1 кг. Масса оранжевого диска - 10 кг, его диаметр - 8 м. Для начальной раскрутки колеса пришлось задействовать силу в 20 н, которая заставила вращаться колесо по часовой стрелке. Но на угловую скорость 9 рад/с колесо вышло только на 1500 секунде. Это подтверждает результаты моделирования колеса Бесслера с 8 грузами, что колесо Бесслера набирает обороты существенно медленнее, чем колесо Альдо Коста.
Подводя некий итог можно считать, что при наличии подходящего механизма перемещения грузов внутри колёса вдоль радиуса или иного способа изменения их момента инерции грузов, колёса будут вращаться. Грузы же в момент перемещения будут терять жесткую связь с основной частью колеса. Значит, мы имеем систему из трех компонентов –
- гравитационное поле Земли,
- вращающееся колесо, которое при вращении создает вращающееся поле центробежных сил,
- груз, которой должен быть перемещен с одной орбиты на другую, который находится в период перемещения под действием силы гравитации и центробежного поля колеса, а, скорее всего, находится в свободном полёте как в том, так и в другом поле.
Всё это пока учёные механики в теоретическом плане, т.е., ученые, занимающиеся теоретической механикой, не проработали. И теории такого процесса еще нет. Тем более не было её и во время Бесслера. Понадобилось более 300 лет на обнаружение этого эффекта. Пока этот эффект обнаружен мной в результате математического моделирования с развитыми средствами визуализации в программе «Живая физика». Теперь требуется подтвердить этот эффект всей мощью, которую накопила теоретическая механика (физика) и физическая математика. А также широкой практикой строительства таких колёс.
Можно считать, что рассмотренные в статье конструкции являются одновременно центробежными двигателями, получающими подпитку из мощного гравитационного поля Земли. Ибо, если исключить из этих конструкций центробежные силы (что невозможно), то одной силы тяжести будет недостаточно для работы гравитационного двигателя.
Не зря я давно утверждал, что вращение, вихрь – это наше будущее и это наше спасение. Только поняв все законы вращения, мы сможем перейти на новые типы энергогераторов, новые средства транспорта, связи и т.д. Только на вихре мы сможем выйти в космос, освоить планеты солнечной системы и отправиться за пределы нашей Галактики.
Теперь прошу просмотреть три фильма по этим ссылкам:
В конструкции устройства, показанного в этих трёх видео, работают идеи Феликса Вюрта (Felix Würth). Это три колеса в колесе. Люди пишут, что не знают, как это работает. Разгадка принципа работы этого устройства очень простая. Скорее всего, это связано с выявленными в процессе моделирования факторами и данными, показанными в этой статье. Ведь все три колеса в колесе вращаются в поле центробежных сил. Тогда каждый резкий поворот центральной маленькой шестерни в нужном направлении равноценен удару по одному из зубьев каждой из трех вращающихся внутри шестеренок с дебалансом. А это можно признать за некий импульс, отражающийся на моменте инерции попавшего под «раздачу» зубца. Направление силы, возникающей при этом, помогает раскручивать шестеренки, а три шестерёнки вместе раскручивают главную шестерню. И тут важно понять, что затраты энергии на повороты малой центральной шестерёнки во много раз меньше той энергии, которую можно будет снять с основной шестерни. Что и демонстрируют эти три небольших фильма.
Стоит также после данного цикла моделирования посмотреть с учетом вновь открывшихся обстоятельств на все «сверхединичные» системы, где используются маховики, а для связи между ними – цепи или ремни. Цепи и ремни охватывают звездочки или шкивы примерно на 50%. И причем с одной стороны. А это значит, что на этой стороне момент инерции звездочки или шкива выше, чем там, где ремня или цепи нет. А в точках, где цепь или ремень начинают охватывать звездочку или шкив, и рождается тот импульс, который увеличивает энергию систему маховиков. Эта тонкость тоже никак не проработана в теоретической механике.
На этом можно поставить точку. Остальное уже должны сделать наши славные инженеры. Ибо теоретическая возможность самовращения колес и колебаний маятников в гравитационном поле Земли доказана. Необычность способа изменения момента инерции грузов в этих маятниках и колёсах объясняет, почему Бесслер и Альдо Коста смогли запустить свои колёса, а до остальных «не дошло» как этот механизм работает. Чтобы не показывать свою глупость и невежество, важные европейские ученые предпочли оклеветать Бесслера. А современные физики стараются не замечать творения Альдо Коста по той же причине.
300 лет великое изобретение Бесслера не смогло из-за невежества ученых стать основным источником энергии нашей цивилизации. В этом виноват и сам Бесслер, который захотел за своё изобретение 20 тысяч талеров. Но с другой стороны просвещенные монархи Европы тоже оказались не лыком шиты, тоже не захотели расставаться с круглой суммой. Вот так, хотели как лучше, а получилось как всегда. Жадность, помноженная на жадность, не доводит до добра. Вот и наше Правительство демонстрирует невежество в экономике и финансах. Вместо того, чтобы разрулить ситуацию, опираясь на денежную эмиссию и власть, наше государство предпочитает ждать от моря погоды, а заодно ведет себя как последний алкоголик и наркоман, продавая обстановку своего дома за небольшую дозу хмельного или наркоты. До следующей ломки!!
Когда же эти либералы оставят нас в покое??? Видимо, пока дуст против паразитов не применить, они сами Россию не покинут!!! Нужно срочно искать санитарного врача и дуст!!!
Все представленные в статье данные дарю всему человечеству. Может быть, среди семи миллиардов людей на Земле найдется всего один, которые соберет где-нибудь в гараже это чуда техники.
Дмитриев сделать это сумел. Правда, он для изменения момента инерции грузов использовал обгонные муфты. Которые позволяли на одной стороне колеса грузам легко под действием сил инерции и центробежной силы отходит от оси вращения колеса, а на другой стороне колеса обгонная муфта заставляла грузы двигаться по траектории, которая была ближе к оси вращения колеса. Механизм другой, но принцип тот же – изменение момента инерции грузов.
Челкалис предложил свой механизм импульсного воздействия на колесо с грузами. И, несмотря на необычность его конструкции, там тоже вполне возможно заложен механизм изменения моментов инерции составных частей его конструкции. Одновременно там может активно работать сила трения, которая в известных случаях тормозит движение тел, а в его конструкции сила трения помогает вращению его колеса.
10 лет я стремился понять, что же заставляло колесо Бесслера вращаться. А еще раньше хотелось создать вечный двигатель или вечный источник экологически чистой энергии, основанной на гравитации, электростатике или магнитном поле. Мне из всех углов твердили, что это невозможно. Но теперь можно смело утверждать, что в принципе эта задача мной решена. Главное же в том, что полностью восстановлена честь великого инженера, механика и моего коллеги – врача. Так что развалинами 300-летнего мракобесия, невежества и умственной лени вполне удовлетворён. Идущим за мной будет уже легче.
Результаты моделирования позволяют надеяться на то, что нам, честным людям, всё же удастся изменить наш мир, нашу Землю к лучшему. А что будем делать с нефтью, газом и углём - этими останками наших предков? Перестанем их сжигать и будем использовать их на благо Жизни на Земле. Даешь вечный двигатель, государственную монополию на денежную эмиссию, запрет наёмного труда и отмену налогов!!! Подлинные и полные знания – в массы!!! Даешь истинную свободу для свободного развития каждого ради свободного развития всех!!!
21.02.2016.