В предыдущих статьях было проведено моделирование разных вариантов маятников и колес. В последней статье «Подведение итогов моделирования маятника Бесслера,
а также колёс Бесслера и Альдо Коста» была сделана, по-моему, успешная, попытка обобщить реакцию колёс и маятников на изменение момента инерции подвижных грузов в необходимой точке относительно колеса, в необходимое время и в необходимом направлении вдоль радиуса.
Обнаружено, что смещение грузов вдоль радиуса относительно оси вращения колеса или колебания маятника может вызвать как замедление вращения колеса или уменьшение амплитуды колебаний маятника, с одной стороны, так и рост частоты вращения колеса или рост амплитуды колебаний маятника, с другой стороны. Главное, выбрать правильное направление для перемещения груза в «критических» точках.
Но некоторые из тех, кому я выслал статью для ознакомления, выразили сомнение, что делать выводы на основании изменения массы подвижных грузов вместо изменения их момента инерции, как это и должно быть, нельзя. Принимаю критику, но считаю, что в предыдущих моделях можно использовать изменение массы в качестве основного параметра. Так как по отношению ко всему колесу при парном количестве подвижных грузов это было равноценно смещению массы в сторону того груза, масса которого увеличивалась со стороны того груза, масса которого уменьшалась. А перемещение массы из одного груза в другой (противоположный) программа «Живая физика» уже учитывала сама как изменение момента инерции, потенциальной и кинетической энергии, и проводила необходимые расчеты.
Для тех, кто всё же продолжает сомневаться в правильности поведения модели, была создана новая модель, которая позволяла последовательно моделировать поведение колеса Бесслера и Альдо Коста с четырьмя грузами, затем число грузов у этих колёс уменьшается до двух. И на последнем этапе моделируется маятник Бесслера. Для этого в колесо Бесслера с двумя грузами добавляется массивный груз, что превращает колесо (качели) Бесслера в физический маятник. У которого изменяется не положение этого добавленного массивного груза, а положение боковых грузов, находящихся на уровне оси маятника, где их перемещение в горизонтальном направлении не потребует много энергии, что снимает всякие возражение о том, что параметрический маятник нельзя использовать в качестве энергогенератора.
Решено было остановиться на простой модели, в которой колесо выглядит как крест, в лучах которого перемещаются подвижные грузы. В качестве силы, которая перемещает грузы и фиксирует их в заданном положении опять выбрана электростатическая сила. Для этого подвижным грузам задается после пересечения горизонтальной или вертикальной оси координат положительный или отрицательный заряд. А в центре креста закреплен диск, положительный заряд которого можно менять. А способность подвижных грузов правильно реагировать на пересечение горизонтальных или вертикальных осей определялась простыми формулами, которые использовались и более ранних статьях.
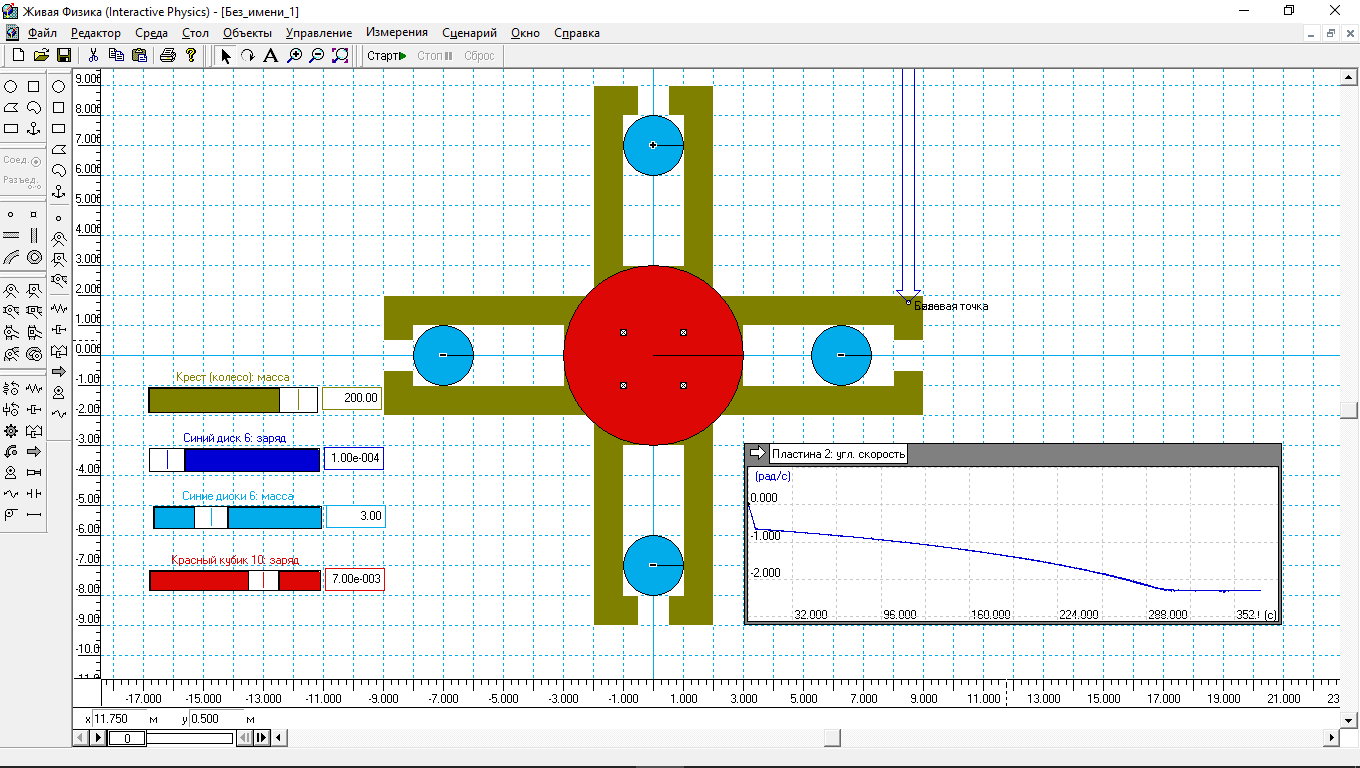
Для начала было проведено моделирование колеса Бесслера с четырьмя грузами. Возможно, в настоящих колесах Бесслера точки для перемещения груза с одной орбиты на другую были другие, а возможно сам Бесслер перепробовал много вариантов колес. Но я решил всё-таки назвать колесо, в котором подвижные грузы перемещаются справа налево или слева направо в крайних горизонтальных точках в зависимости от направления вращения колеса. Ибо такое перемещение требует небольших энергетических затрат. Модель показана на рис.1.

Рис.1
На рис.1. показан скан окна программы после проведения моделирования и нажатия на кнопку «Сброс». Модель – это крест, в лучах которого могут перемещаться подвижные грузы под действием электростатических и центробежных сил. В центре колеса установлен и закреплён заклепками красный диск, он заряжен положительно, значение заряда определяется регулятором красного цвета (это справа в самом низу). В данном случае заряд красного диска равен 7e?3к. Масса голубых дисков определяется регулятором голубого цвета. В данном случае масса голубых дисков равна 3 кг.
Заряды голубых дисков определяются регуляторам синего цвета. Значение заряда голубого диска в зависимости от положения равно 1e-4 или -1e-4. Формула для этого заряда следующая:
if(Body[7].p.y>0,Input[26],-Input[26]) (1)
Body[7].p.y – значение Y-координаты для диска [7], Input[26] абсолютная величина заряда голубого диска, определяемая регулятором Input[26].
Значение зарядов грузов и красного диска можно устанавливать в широких пределах. Масса самого креста (колеса) равна 200 кг. Такая масса выбрана для более равномерного вращения колеса. На правое крыло в течение 10 с действует сила в 10 н для того, чтобы запустить колесо во вращение. После 10 с сила действовать перестает, что отражается на её внешнем виде – её контуры становятся пунктирными.
Результат моделирования отражён на индикаторе справа от креста. Колесо вращается по часовой стрелке. Видно, что в течение 10 с угловая скорость колеса быстро нарастает. Затем в течение примерно 280 с колесо увеличивает угловую скорость по параболе, а потом постепенно угловая скорость стабилизируется примерно на уровне 2.2 рад/с. Это связано с тем, что центробежная сила начинает превышать силы электростатического притяжения между подвижным диском и красным диском. Гладкость кривой отражает аккуратность визуальной модели. При других параметрах – массе и заряде голубых дисков, заряде красного диска, а также массе креста кривая будет иметь другой вид, на раскрутку колеса потребуется больше или меньше времени. Но три этапа нарастания угловой скорости и рост угловой скорости по параболе останутся в любом случае.
Если внимательно присмотреться, то можно увидеть знак заряда на голубых дисках.
Теперь промоделируем колесо Альдо Коста, в котором перемещение грузов осуществляется в нижней и верхней точках колеса (рис.2).
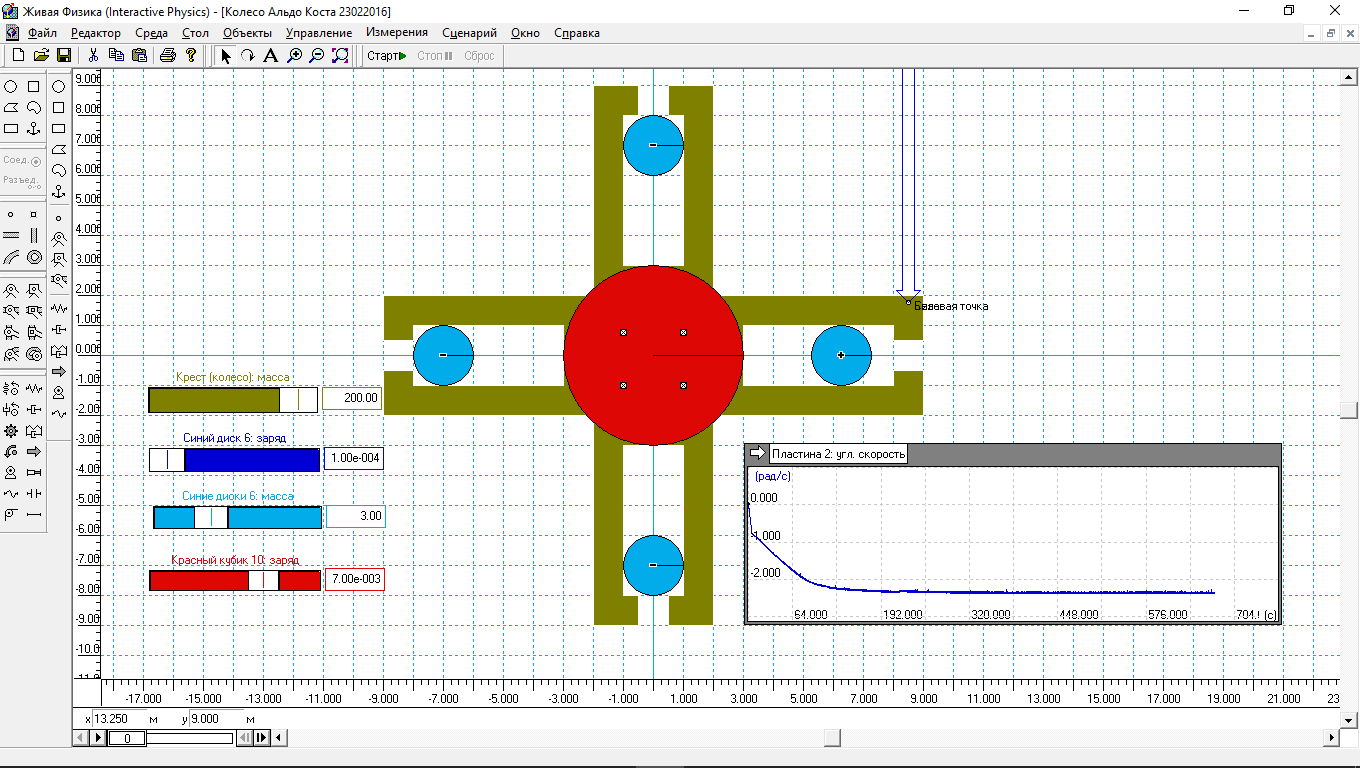
Рис.2.
Здесь практически те же параметры – масса и величина заряда подвижных грузов, величина заряда красного диска, масса креста. Но в голубых грузах в параметре «заряд» заложена формула:
if(Body[7].p.x>0,Input[26],-Input[26]) (2)
Body[7].p.x – значение X-координаты для диска [7], Input[26] абсолютная величина заряда голубого диска, определяемая регулятором Input[26].
Чтобы колесо Альдо Коста вращалось против часовой стрелки, сила должна быть направлена вверх, а формула должна иметь другой вид:
if(Body[7].p.x<0,Input[26],-Input[26]) (3)
Да и сила должна иметь противоположное направление.
Результат моделирования зафиксирован на индикаторе справа. В течение 10 с крест (колесо) разгоняются принудительно, затем начинается интервал, в течении которого колесо набирает обороты. Но теперь график напоминает логарифмическую кривую. Угловая скорость вначале нарастает практически линейно, затем рост постепенно замедляется и, в конце концов, угловая скорость креста (колеса) достигает 2.2 рад/с. И длительное время упорно держится на этом значении. В целом данная модель ведет себя так же, как и те, о которых написано в более ранних статьях.
Теперь оставим в модели всего два противоположных груза. И посмотрим, как будет себя вести такое колесо (крест). Для этого уберем два голубых диска – верхний и нижний, и закрепим их якорем в левом верхнем углу окна программы. Не забудем снять с них заряд. Оставим на кресте правый и левый голубые диски.
Чтобы упростить, вначале промоделируем простую модель колеса Альдо Коста. Это затем, чтобы воспользоваться уже введенными формулами в голубые диски. Результат моделирования показан на рис. 3.
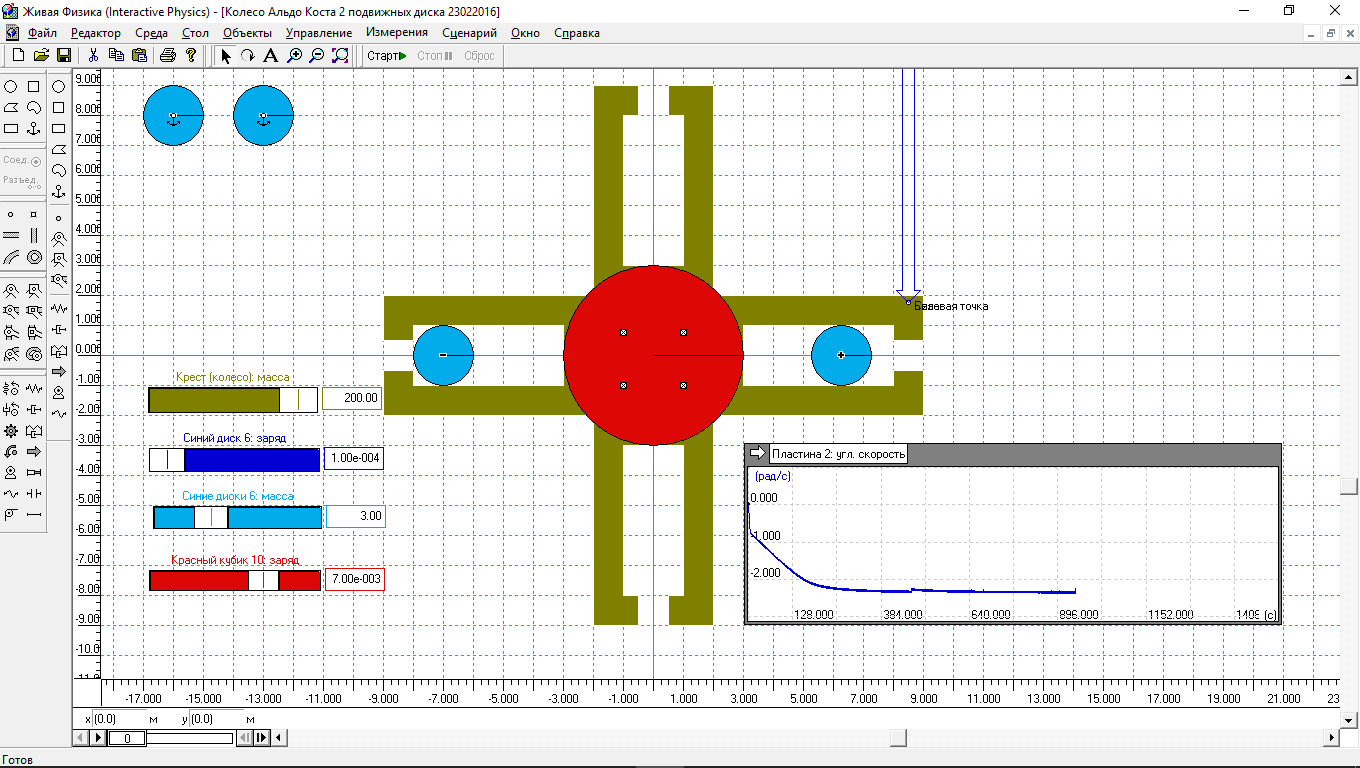
Рис.3.
Результат моделирования креста (колеса) Альдо Коста с двумя подвижными грузами практически не отличается от результата моделирования колеса с четырьмя грузами. Это и понятно, так как масса креста 200 кг, и снятия с колеса 6 кг особой роли не играет. Также примерно за 130 с колесо выходит на предельную угловую скорость. А предельная угловая скорость определяется величинами зарядов голубых и красного дисков, а также массами голубых дисков. Они не изменились, поэтому и предельная угловая скорость креста (колеса) не изменилась. На 900 с один из голубых дисков сорвался с креста и улетел по касательной. Поэтому эксперимент пришлось прекратить.
Теперь проведем моделирование колеса Бесслера с двумя подвижными (голубыми) дисками (рис.4). Формула для подвижных дисков, управляющая зарядом голубых дисков была преобразована в формулу (1).
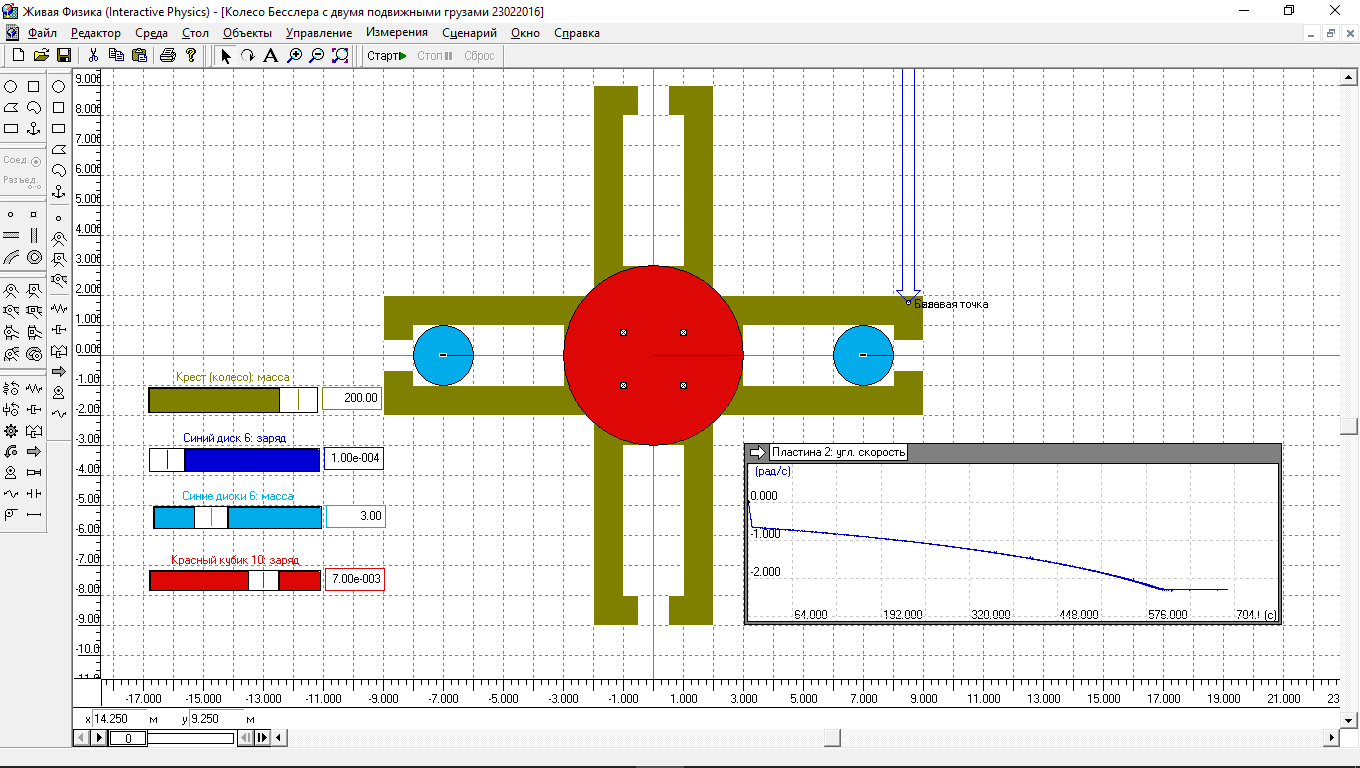
Рис.4.
Эта модель показывает зависимость от числа подвижных грузов. Если при четырёх грузах колесо Бесслера достигла своей предельной частоты за 300 с, то при двух грузах предел достигнут за 600 с – 10 мин. Предельная угловая скорость – 2.3 рад/с.
Сравнивая колесо Бесслера с колесом Альдо Коста можно увидеть, что смещение центра тяжести колеса вправо или влево от вертикальной оси позволяет колесу быстрее набирать необходимую частоту. В принципе, сам Бесслер вполне мог в одно из своих колёс встроить механизм по смещению грузов вдоль радиуса в нижней и верхней точках колеса. Несмотря на то, что задача конструирования механизма, позволяющего это реализовать непосредственно в самом вращающемся колесе и на механическом уровне, достаточно сложна, эту задачу необходимо решить. И чем проще будет механизм, тем лучше. Можно использовать электромагниты. Использование в программе электростатики связано с тем, что программа допускает использование этого инструмента наиболее простым способом. Мне был важен сам принцип. Теперь, когда знаешь, как правильно смещать подвижные грузы для поддержания самовращения колеса, можно думать о конкретном механизме, который будет управлять перемещением грузов.
Теперь осталось провести моделирование параметрического маятника Бесслера (рис.5).
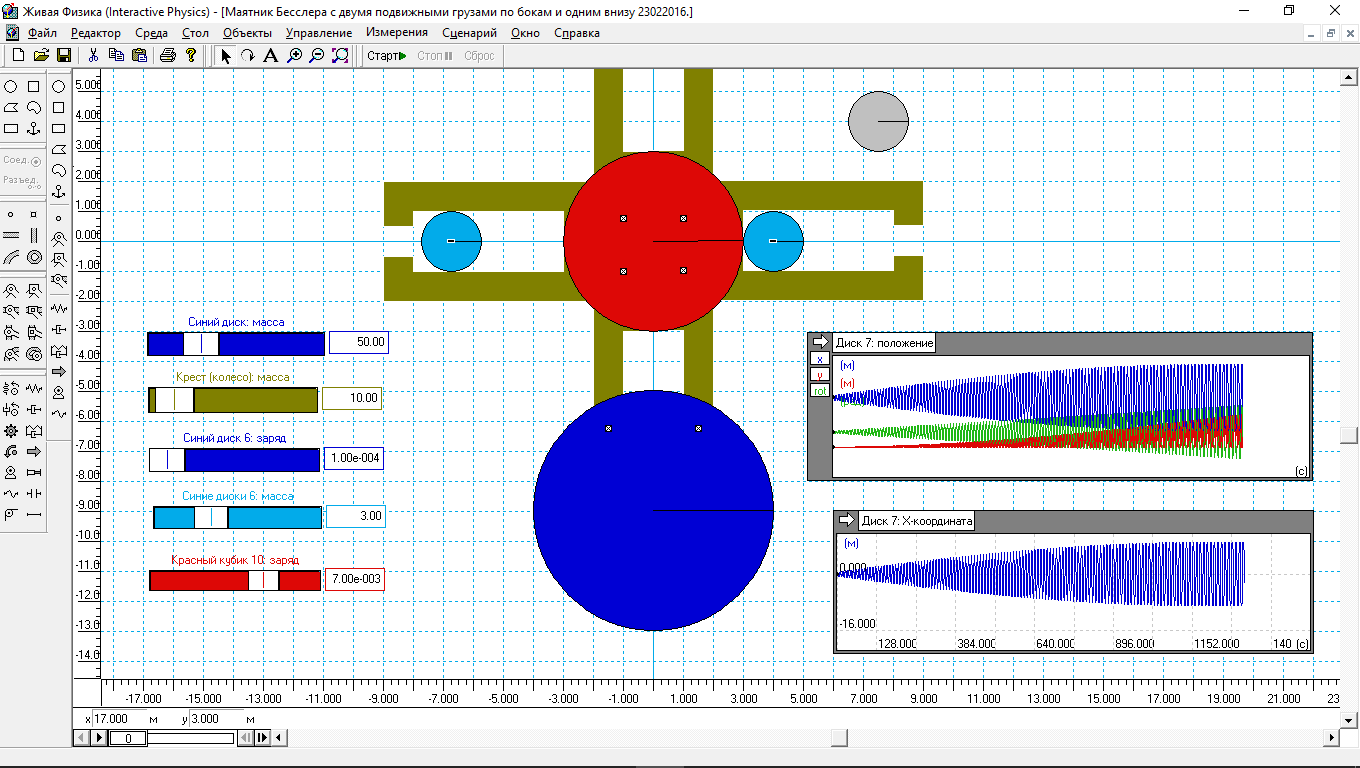
Рис.5
За основу взято колесо Бесслера с двумя голубыми грузами. В каждом голубом грузе величина и знак заряда определяется по формуле (1). Добавлен синий диск в качестве нижнего груза. Его масса задаётся самым верхним регулятором справа от модели. Масса креста выбрана в 10 кг, масса голубых дисков по 3 кг, масса синего груза – 50 кг. Заряд голубых дисков по модулю равен 1e-4к, а заряд красного диска – 7e-3к. Размеры маятника, как и уже промоделированных колёс можно определить по линейкам внизу и слева окна программы. Запускается процесс сбросом серого диска, масса которого в пределах 3-5 кг. Точное значение не фиксировалось.
Результат моделирования можно посмотреть на индикаторах справа от модели. Видно, что вначале амплитуда колебаний маятника по горизонтали (по оси X) были в пределах нескольких сантиметров. Но примерно через 1000 с амплитуда достигла 7 м по горизонтали, а по углу отклонения совершались в пределах -100 до +100 градусов. Эксперимент был прерван на 1300 секунде, и хотя рост отклонений, выраженных в радианах (градусах) практически стабилизировался, но полностью на этом рост не закончился.
Всё это дает основание утверждать, что параметрический маятник может быть больших размеров. Что довести его до максимальной амплитуды можно энергомалозатратным способом, смещая боковые подвижные грузы параллельно поверхности Земли, а точнее перпендикулярно направлению силы тяжести в точке установки маятника. Данный способ параметрической накачки маятника отличается от того, что обычно приводится в учебниках физики, где параметрический резонанс регулируется уменьшением момента инерции физического маятника при прохождении маятника самых нижних участков траектории. Чтобы были понятны отличия предлагаемого мной способа параметрического воздействия на физический маятник, хочу привести результат моделирования (упрощенного) физического маятника, когда при движении по самым низким участкам траектории его центр тяжести приподнимается против силы тяжести. На это, естественно, затрачивается энергия, но тут надо обязательно проверить, сколько энергии тратится на управление момента инерции такого маятника и сколько с него можно снять энергии. Это еще, похоже, по большому счёту, никто не делал. А не мешало бы.
Привожу результат моделирования такого маятника (рис.6).
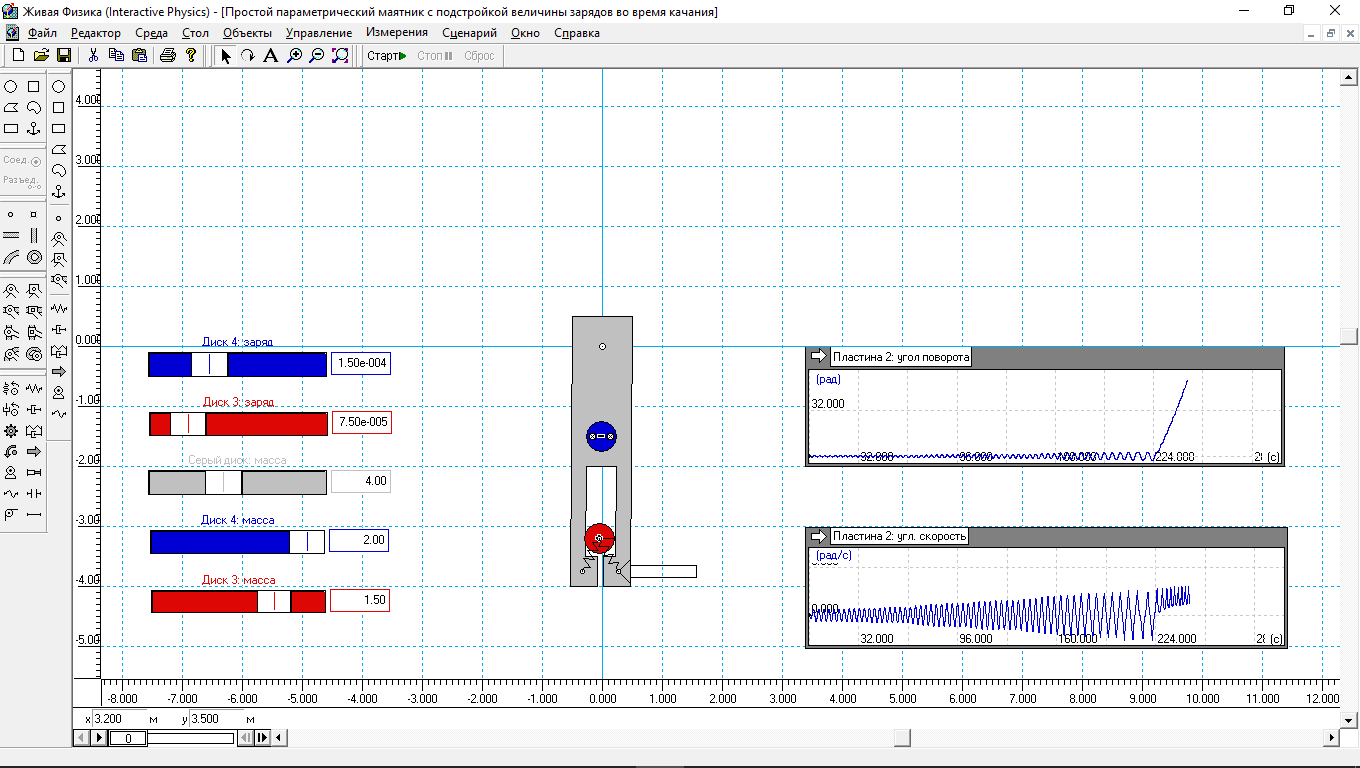
Рис.6.
Маятник простой, пластина (брусок) с прорезью в нижней части, по которой скользит красный диск, закрепленный снизу двумя пружинами. Пружины уже настроены так, что они немного поджимают красный груз к краю маятника (прорези). Масса красного груза 2 кг. Начальный заряд красного диска 7.5e-5к, затем по мере раскачки из-за центробежной силы приходилось вручную постепенно увеличивать до 3e-4, чтобы иметь возможность наращивать амплитуду колебаний маятника. Наверно, можно было бы заложить в модель возможность изменять заряд красного диска в зависимости от центробежной силы. Для этого надо писать специальный сценарий, а времени и желания у меня не было. Проще было проделать все манипуляции вручную.
Заряд синего диска изменялся по формуле:
-Input[14]*abs(cos(Body[2].p.r)) (3),
Где Input[14] – значение синего регулятора Input[14], Body[2].p.r – угол отклонения серого бруска от горизонтали по часовой стрелке.
В результате заряд синего диска изменялся так, что максимальное его значение было тогда, когда серый брусок принимал вертикальное положение, а когда он принимал горизонтальное положение, то заряд обнулялся. Поэтому в вертикальном положении сила притяжения синего и красного дисков максимальна, при отклонении сила притяжения уменьшалась. Как ведет себя сила притяжения между синим и красным дисками, меня особо не волновало, так как понимал, что всегда можно ограничением величины красного заряда ограничить амплитуду колебаний этого физического маятника в пределах от -90 до +90 градусов.
После запуска процесса в ручном режиме, постепенно наращивая заряд красного диска, удалось довести маятник до вращения, то есть превратить маятник в колесо, где был всего один подвижный диск. Что и подтверждает мое неоднократное замечание, что колесо можно сделать из одного перемещаемого вдоль радиуса груза. Лишь бы была правильно сконструирована, как пишет Альдо Коста, система по смещению груза в нужном месте, в нужное время и в нужном направлении. Данную модель удалось раскрутить на 360 градусов на 224 секунде.
Чтобы желающие могли поиграть в данные модели, даю ссылки на файлы этих моделей в формате, пригодном для запуска в программе «Живая физика». Запускать модели желательно в программе с русским интерфейсом, так как в английском варианте индикаторы имеют другой формат. После загрузки в такую программу с моделью работать можно, а вот при сохранении результатов иногда пропадают индикаторы. Так что надо быть внимательным, чтобы потом не пришлось самому устанавливать нужные индикаторы в случае их исчезновения. Вот ссылки на модели:
1. Модель колеса Бесслера с 4 грузами. (Скачать)
2. Модель колеса Бесслера с 2 грузами. (Скачать)
3. Модель колеса Альдо Коста с 4 грузами. (Скачать)
4. Модель колеса Альдо Коста с 2 грузами.(скачать)
5. Модель параметрического маятника Бесслера.(скачать)
6. Модель простого физического параметрического маятника.(скачать)
7. Вторая модель простого физического параметрического маятника.(скачать)
8. Видео о работе маятника (качество низкое) (скачать).
9. Видео о результате раскачки маятника ((скачать).
Вот так, с горем пополам удалось, пытая модель, нащупать способ параметрического возбуждения колебаний маятника, типа того, что применял Бесслер в своём колесе. Не уверен на 100%, был ли у Бесслера маятник параметрическим, но моделируя его колесо, я неожиданно для себя обнаружил вроде бы странный способ параметрического возбуждения колебаний как маятника, так и самовращения колеса. Всё это подробно описано сразу в нескольких статьях.
Некоторые критики высказывают мнение, что программа «Живая физика» могла ошибиться. Не думаю, ибо в эту программу заложены все те же алгоритмы, которые используются в самых лучших математических программах, таких как MathCAD или Math lab, например. Не может быть, чтобы программа, которая правильно моделирует простой параметрический физический маятник, неправильно моделирует параметрический маятник немного иной конструкции, в котором по-иному происходит смещение частей маятника в зависимости от положения их относительно горизонта или вертикальной линии.
Одновременно удалось провести моделирование колеса Альдо Коста, выявлены особенности его поведения, которые, несмотря на бОльшие затраты на перемещение грузов в самой нижней и самой высокой точке колеса, заслуживают внимания. Это колесо должно стать объектом пристального внимания физиков, как потенциальный источник механической, а значит и электрической энергии, способный при необходимости очень быстро наращивать мощность. В этом отношении колесо Бесслера (так я его назвал) уступает колесу Альдо Коста, хотя максимальные мощностные показатели этих колес при прочих равных условиях одинаковые. Маятник Бесслера тоже заслуживает внимание физиков, ибо при достаточных габаритах этот механизм может стать мощным источником энергии, который будет легко обслуживать. Что касается неравномерности вращения, которое можно получить с такого маятника, то тут можно задействовать супермаховик Гулиа, который будет заряжаться от параметрического маятника, а отдавать энергию по мере появления в ней потребности. Придется подумать над тем, куда девать лишнюю энергию.
Параметрические маятники и колеса могут стать эффективными источниками механической и электрической энергии, которым не нужен пар, нефть, газ, нефтепродукты (бензин, дизельное топливо) или уголь. Меня удивляет, что учёные до сих не осмелились освоить параметрический резонанс в промышленных масштабах. Наоборот, везде, где можно с параметрическим резонансом борются, как с вредным явлением, способным нанести вред людям. Частью они правы, но вместе со страхом перед возможными разрушениями вместе с грязной водой выбрасывается ребенок – возможность создания безтопливных источников энергии, которые опирались бы на широко известные физические поля – гравитационное, электростатическое и магнитное. А ведь еще высокое давление, которое можно создать под водой, глубоко погрузившись под воду или создав его в замкнутом пространстве с помощью газовой (воздушной) подушки. И насколько я знаю, кое-кто работает в этом подводном направлении. Например, Марухин со своими товарищами.
Сравните, Саяно-Шушенскую ГЭС или Чернобыльскую АЭС с парками самовращающихся колес или маятников, на строительство которых, скорее всего, потребуется меньше ресурсов и финансовых средств. Об эксплуатационных расходах и говорить нечего. Кроме того, колеса и маятники гораздо безопаснее для природы, людей и животных. Ну, сломается одно колесо, его легко починить и вновь запустить. Энергосистема даже не заметит аварии. А если создавать такие колесные и маятниковые энергопарки под землёй, то останется построить, закопать и на долгое время забыть об их существовании. А вот энергию они будут исправно выдавать почти даром.
Нет, кое-что в плане использования параметрического резонанса делается. Например, это можно обнаружить в электронике. Но используемые там мощности небольшие, в качестве источников энергии эти электронные устройства не годятся. Кое-кто пытается разгадать загадки, оставленные Тесла. И там, скорее всего, работает параметрический резонанс. Капанадзе намекал, что он открыл резонанс в резонансе, поэтому ему удалось создать генератор чистой энергии. А это означает, что частота задающего (возбуждающего) генератора и разрядника в трансформаторе Тесла должна быть в два раза выше, чем в основном контуре. И частота и фаза в задающем контуре, работающего в импульсном режиме, должна непрерывно подстраиваться под частоту в основном контуре. Так как по мере раскачки параметрического резонанса частота колебаний в основном контуре может довольно сильно вырасти, и отклониться от той частоты, которую обычно приводят в учебниках для контура, состоящего из конденсатора и индуктивности.
Параметрические источники энергии могли бы решить многие проблемы в отдаленных регионах России, многочисленных «заброшенных» населенных пунктах, отдаленных гарнизонах, больших кораблях и даже самолётах, подземных пунктах управления МО. Механические параметрические системы, которые можно строить уже сейчас, могли бы расщеплять воду на водород и кислород круглые сутки и круглый год, а излишек электроэнергии отдавать в централизованную сеть.
Со временем промоделированные в данной статье колеса и маятники могли бы заменить генераторы на ГЭС, ТЭС, АЭС. Реки освободятся от плотин. Недра не будут разоряться ради нефти, газа и угля. Не надо будет людям рисковать своими жизнями ради урана и прочих радиоактивных элементов. Системы жизнеобеспечения станут более независимыми, каждый дом и даже каждая квартира могла бы иметь свой источник энергии, если поставить это на промышленную основу. Думаю, что общие сети – газ, электроэнергия, вода, тепло – сразу разобрать не получится, они будут служить людям до тех пор, пока стоимость ремонта не заставит владельцев заменить их на более современные системы. Но если до сих пор многие просто не знали, чем их можно заменить, то теперь альтернатива появилась – это системы, основанные, например, на параметрических маятниках и самовращающихся колёсах, но и параметрические системы, основанные на других принципах, со временем тоже будут освоены.
Уверен, что время АЭС, ГЭС и ТЭС заканчивается. Видимо, будут закрываться ветропарки и СЭС (солнечные электростанции). Так как ветровая и солнечная энергия непостоянны и их потоки не обладают высокой мощностью, стоят очень дорого, загрязняют окружающую среду и трудоёмки в обслуживании и ремонте. Их стоимость превышает стоимость ГЭС и ТЭС. Бедная Африка и Китай, куда западный мир сплавляет всю списанную электронику, солнечные батареи и прочие «нештяки» нашей цивилизации.
Хочу добавить, что параметрический маятник является замечательным примером того, как организовать некий колебательный процесс с помощью другого колебательного процесса меньшей мощности и направленного перпендикулярно главному процессу. А перпендикулярность процессов, а точнее потоков энергии - это главный признак того, что маломощный процесс управляет мощным и одновременно запитывается от него напрямую или через вспомогательные устройства. В частности в данном параметрическом маятнике Бесслера колебания задающий генератор осуществляет по горизонтали, а основной осциллятор (большой груз) совершает колебания по вертикали, хотя и движется по дуге окружности. И поэтому этот маятник при определённом наборе параметров легко переходит во вращение, превращаясь в колесо.
Что касается того, откуда энергия берется? Можно сказать, что ниоткуда. Ибо в любом колебательном процессе регулярно положительное меняется на отрицательное, что в сумме по целому числу периодов дает энергетический ноль. Но человек от этих колебаний берет часть энергии, выпрямляет её, использует, и в дальнейшем может выбросить в окружающую среду, где она постепенно рассосётся и обнулится.
Что касается управляющего осциллятора, то его энергия тоже в сумме за некое число полных периодов практически равна нулю. Так что и тут полный ноль.
Вывод. Любая энергия ни откуда не берется и никуда не исчезает. И то, что мы называем потоками энергии - это только жалкая часть из половины тех потоков, которые шастуют туда-сюда в эфире. Но они часто не проявляют себя, так как все потоки эфира, какими бы мощными не были имеют своего двойника, который движется в противоположном направлении. Любой вихрь всегда имеет парный вихрь, но с противоположным направлением вращения. И т.д. То есть, если потока энергии нет, то его надо замутить.
Надо не только уметь извлекать энергию из существующих природных потоков, но и создавать вихри из "стоячего" эфира и использовать энергию либо обеих вихрей сразу или только одного, а энергию второго оставить на усмотрение природы (самого эфира). И создать два вихря в эфире или иной среды можно только с помощью параметрического резонанса.
Физики пока еще этого в полной мере не понимают. Они рассматривают параметрический резонанс только на уровне игрушек. А это похоже на то, что в Центральной Америки знали колесо, но Боги разрешали делать из них игрушки, но взрослым использовать колёса запрещали.
Наблюдая за деятельностью некоторых физиков и изобретателей, я могу отметить, что они не уделяляют должного внимания параметрическому резонансу. Практически всегда они работаете с обычным резонансом, а это всё равно, что воду в ступе толочь. Надо работать с параметрическим резонансом. А у него один критерий - частота колебаний задающего генератора должна быть в два раза выше частоты колебаний в основном генераторе. И частоты генераторов должны автоматически подстраиваться друг к другу. Фаза тоже имеет значение, как и желательность, чтобы в задающем генераторе формировались положительные короткие по продолжительности импульсы. Тогда за счет небольшой затраты энергии можно раскачать любую колебательную систему, охватив её всю солнечную систему как минимум.
Параметрические колебания можно возбудить только в системе, которая находится под давлением, напряжением или иным постоянным силовым воздействием как природного (атмосфера, электростатическое поле Земли, гравитационное поле Земли, подводный мир и т.д.), так и рукотворного характера (воздушный пузырь в бочке с водой, мешок картошки, или домкрат). И тут нам очень повезло, ибо эфир, среда, из которой мы состоим, и внутри которой существует вся вселенная, находится под очень польшим давлением. Поэтому возбуждать в нём колебания не просто, а очень просто. Эфир постоянно вибрирует на самых разных частотах и всегда готов откликнуться на любую из них. Одни колебания мы можем регистрировать своими органами чувств, другие можем улавливать специальными детекторами и приборами. Одним из инструментов, с помощью которых можно раскичивать эфир, является разрядник. С его помощью одни физики (Герц) доказали существование электромагнитных волн, а Тесла мог управлять уже очень мощными потоками эфира, которые многими учеными и дилетантами принимаются за особые формы электричества. Хотя с другой стороны разные формы электричества и магнетизма - это просто формы существования эфира.
Завершая статью, можно смело утверждать, что Французская академия, запретив изобретение вечных двигателей, оказалась не права. Запрет был сделан, исходя из чисто формальных соображений. То же самое, якобывторная было в Центральной и Южной Америке, где боги запретили людям использовать колесо. Сегодня в России зверствует комиссия по борьбе с лженаукой. И тоже запрещает всё, что вращается. Видать в этом есть нечто символичное. Запрещая колесо и вечные двигатели (вечное движение), боги, французы и власть, не хотят, чтобы люди обрели подлинную свободу, смогли совершить рывок в научно-техническом развитии, мешают выйти в космическое пространство и приступить к колонизации ближайших к Земле планет солнечной системы и их спутников.
Особо радует меня, что Бесслер был прав. Теперь он полностью реабилитирован. Пусть еще не построено настоящее колесо из металла, камня и дерева, но уже есть направление, по которому надо идти. Так что это уже дело времени. Тайна Бесслера раскрыта и она оказалась совершенно не такой, какой её представляли и представляют многие исследователи.
Надеюсь, что другие авторы и настоящие учёные займутся колесом Бесслера и Альдо Коста, а также параметрическим маятником более основательно, чем это было сделано мной. Первый шаг сделан, теперь всем предстоит долгая дорога, но на неё будет энергия, свет, вода, водород и кислород, пищевое изобилие, нормальные справедливые отношения между людьми. Ростовщики должны быть уничтожены как класс. И они будут уничтожены, но ненасильственными методами. Это сделает свободная энергия и свободный доступ к ней всем желающим и нуждающимся. Сбывается тысячелетняя мечта человечества. Мы незаметно даже для себя входим в новый мир, где энергия перестанет быть лимитирующим фактом. И это будет самой нужной и самой главной революцией в истории человечества, которая, не разрушая ничего, создаст совершенно новый мир - совершенный мир.
Размешено 23.02.2016