Рис.1. Результат моделирования колеса без тросов.
Занявшись моделированием гравитационного колеса Бесслера в программе «Живая физика», я пришёл к выводам, что способов параметрического возбуждения гравитационного колеса минимум три. И все они, естественно, требуют своих конструктивных решений. Некоторые из них, если ограничиваться уровнем механики и той формой колеса, которым оперировал Бесслер, могут оказаться довольно сложными. Другие способы, наоборот, могут быть решены, особенно, для параметрического маятника довольно просто.
Но если мы будем использовать для перемещения подвижных грузов в нужном месте, в нужное время и в нужном направлении электромагниты, а в качестве подвижных грузов будем использовать железные болванки, шары или цилиндры, то тогда все варианты уже будут решаться практически одинаково. И при использовании интеллектуальных систем управления дело будет сводиться к замене одной программы на другую.
Важно отметить, что для «раскрутки» до предельной частоты массивного колеса не обязательно использовать тяжелые грузы. Для колеса общей массой 500 кг достаточно 4 подвижных грузов в 1-2 кг, чтобы довести угловую скорость колеса для 2-3, а то и более радиан в секунду. Возможно, для некоторых это покажется небольшим показателем. Но если принять, что модели были размеров 20х20 м, то такая угловая скорость уже не покажется маленькой.
Наблюдая за поведением подвижных грузов, обратил внимание на то, что предельная угловая скорость вращения колес зависит от массы подвижных грузов. Если масса грузов небольшая, то угловая скорость при прочих равных условиях оказывалась выше. При увеличении массы подвижных грузов максимальная угловая скорость снижалась. Видимо, предел для угловой скорости зависел не столько от массы, сколько от момента инерции, которая создавалась подвижным грузом.
Кроме того, параметрический резонанс требовал от парных грузов синхронного одновременного смещения на одинаковое расстояние вдоль радиуса колеса. Если один из грузов смещался, например, на один метр дистальнее, то второй (парный) должен смещаться проксимальнее относительно оси вращения колеса. Из-за роста центробежной силы при увеличении угловой скорости вращения колеса это правило нарушалось и в конце концов наступал момент, когда центробежная сила заставляла грузы равноудалиться от оси вращения колеса и перестать реагировать на попытки системы управления переместить подвижные грузы в заданную позицию. А раз уже грузы оставались в фиксированном положении, то рост угловой скорости больше уже не наблюдалось, соответственно, не росла и мощность колеса.
Поэтому целью данной серии экспериментов с моделью гравитационного колеса стала проверка влияния тросов и пружин на мощность колеса, в котором парные грузы связаны друг с другом тросами, а с колесом пружинами. Но, естественно, перемещение грузов осуществляется посредством управления знаком и величиной заряда зелёных грузов.
Для этого была «собрана» очередная модель, которая позволяла использовать её как в варианте колеса, так и в варианте маятника. Вначале модель была проверена без тросов между парными грузами (рис.1).

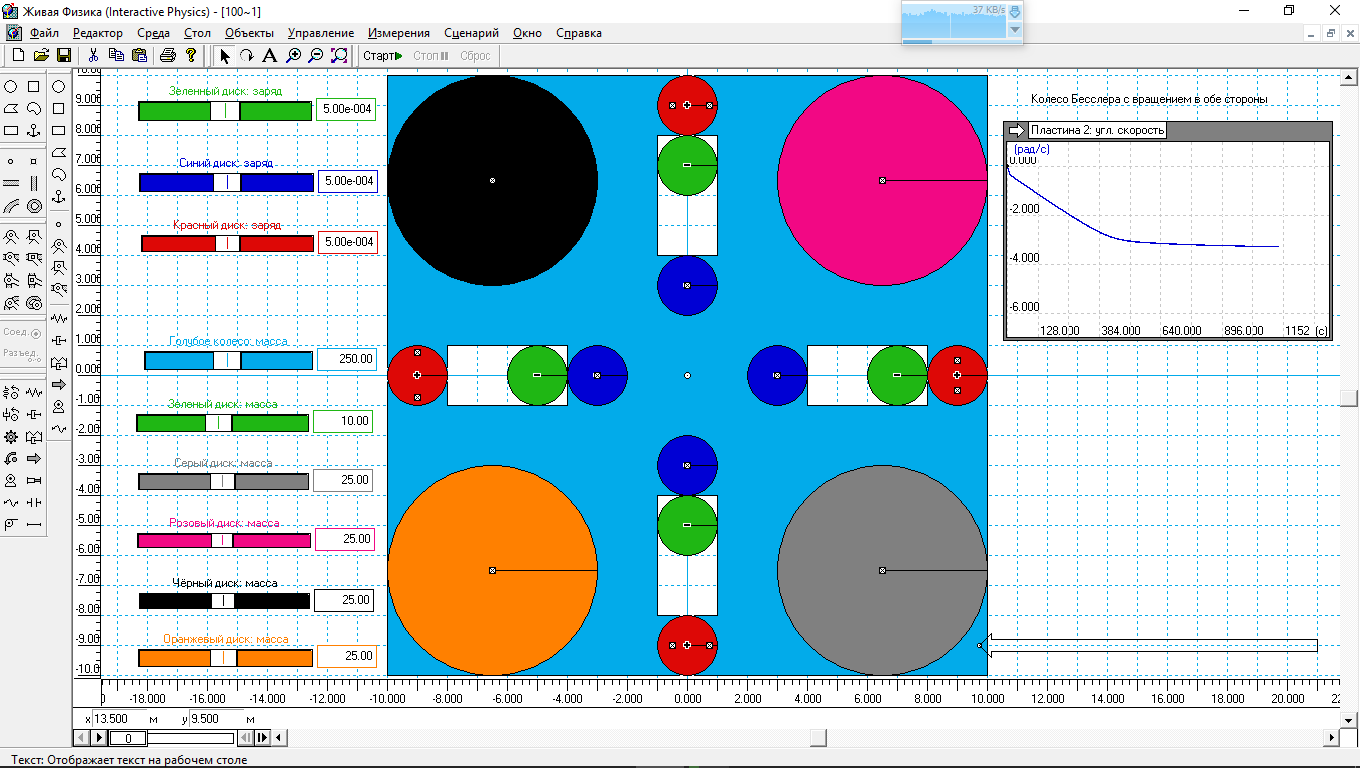
Рис.1. Результат моделирования колеса без тросов.
На этот раз за основу колеса была взята квадратная пластина, в которой были проделаны щели для перемещения подвижных грузов по задаваемой заранее программе. В качестве инструмента для перемещения грузов была вновь использована электростатика. По углам квадратного колеса размещены габаритные грузы.
Колесо запускается силой внизу справа, её величина примерно равна 80 н, время действия 10 с.
Получилась, вообще-то, интересная конструкция, которая наложила некоторые ограничения на формулы, которые должны были управлять зарядами зеленных подвижных дисков в целях обеспечения их перемещения. Поэтому был выбран вариант, который прекрасно себя показал при моделировании классического физического маятника. Формула для поля «заряд» левого зеленого диска следующая:
if(body[6].p.x*body[6].v.r>0,Input[77],-Input[77]) (1)
Хотz эта формула определяет заряд зеленного диска, но критерий, по которому происходит перемещение зелёного диска в другую позицию, определяется положением и угловой скоростью соседнего с ним красного диска. Body[6].p.x – это X-координата красного диска, а body[6].v.r – это угловая скорость красного диска относительно оси колеса. Input[77]- это абсолютная величина заряда зеленного диска, значение которого определяется регулятором под номером [77]. На рис.1. это самый верхний регулятор слева от модели колеса. Два других регулятора ниже первого позволяют задавать величины зарядов красных и синих дисков. Все три регулятора настроены на одинаковое значение – 5e-4 к. Когда модель «работает», то знаки зарядов на красных, зелёных и синих дисков прекрасно видны. Видно также, как меняется заряд у зелёных дисков с “+” на “-” и обратно.
Этот вариант управления перемещением подвижных зелёных грузов выбран потому, что в режиме маятника у этой конструкции использование других формул становится невозможным. Так как в таком случае начальные перемещения подвижных грузов должны совершаться под углом в 45 градусов к вертикали и горизонтали. А в таких позициях не работают другие алгоритмы, «заточенные» на пересечение центром грузов вертикали или горизонтали. Поэтому решено использовать формулу (1), так как она «работает» по более общим признакам – в какой полуплоскости находится управляемый диск – в левой или правой, а также, куда вращается диск – по часовой стрелке или против часовой. Поэтому, если диск поднимается, то он смещается к центру, уменьшая момент инерции, если опускается, то смещается на периферию, увеличивая момент инерции. Если этот алгоритм используется при моделировании маятника, то поведение подвижного груза «пародирует» поведение человека на взрослых качелях.
Остальные регуляторы задают массу компонентов, из которых состоит колесо. Голубой регулятор определяет массу голубой квадратной платины, основу колеса. Масса её равна 250 кг. Размеры 20х20 м. Масса зелёных подвижных грузов составляет 10 кг. Масса каждого большого диска по углам колеса составляют 25 кг. 4 диска – это уже 100 кг. Таким образом, колесо размером 10х10 м и массой более 350 кг вращается 4-мя грузами по 10 кг (всего 40 кг).
Индикатор справа от модели отражает динамику угловой скорости всего колеса. Четко видно, что предельная угловая скорость примерно равна чуть более 3 рад/с. При этой угловой скорости подвижные зелёные диски прижимались к периферии колеса и переставали перемещаться вдоль радиуса, что делало невозможным осуществление параметрического резонанса.
Во время просмотра процесса моделирования такого колеса и возникла идея соединить тросом или прутом противоположные парные груза. Идея состояла в том, что в таком случае грузы будут смещаться синхронно, и помогать друг другу в преодолении центробежной силы. Действительно, при высокой частоте вращения смещающийся к периферии груз без проблем тянул бы за собой парный с ним груз, который должен быть смещен к центру колеса.
Вначале была сделана попытка использовать такой элемент, как прут. Вроде бы решение правильное. И поначалу модель вела себя без всяких «фокусов». Но внезапно при повышении угловой скорости произошло самопроизвольное удлинение одного из прутов. Такое поведение прута мне не понравилось. Либо это сбой в программе, либо, действительно, прут, как конструктивный элемент программы, имеет некий известный программе предел текучести и прочности, преодоление которого вызывает необратимую деформацию (удлинение) прута.
Поэтому пришлось остановить свой выбор на тросе. Тем более у троса должен быть выше такой показатель как прочность на разрыв.
Результат моделирования колеса, в котором парные грузы связаны тросами, показан на рис.2.
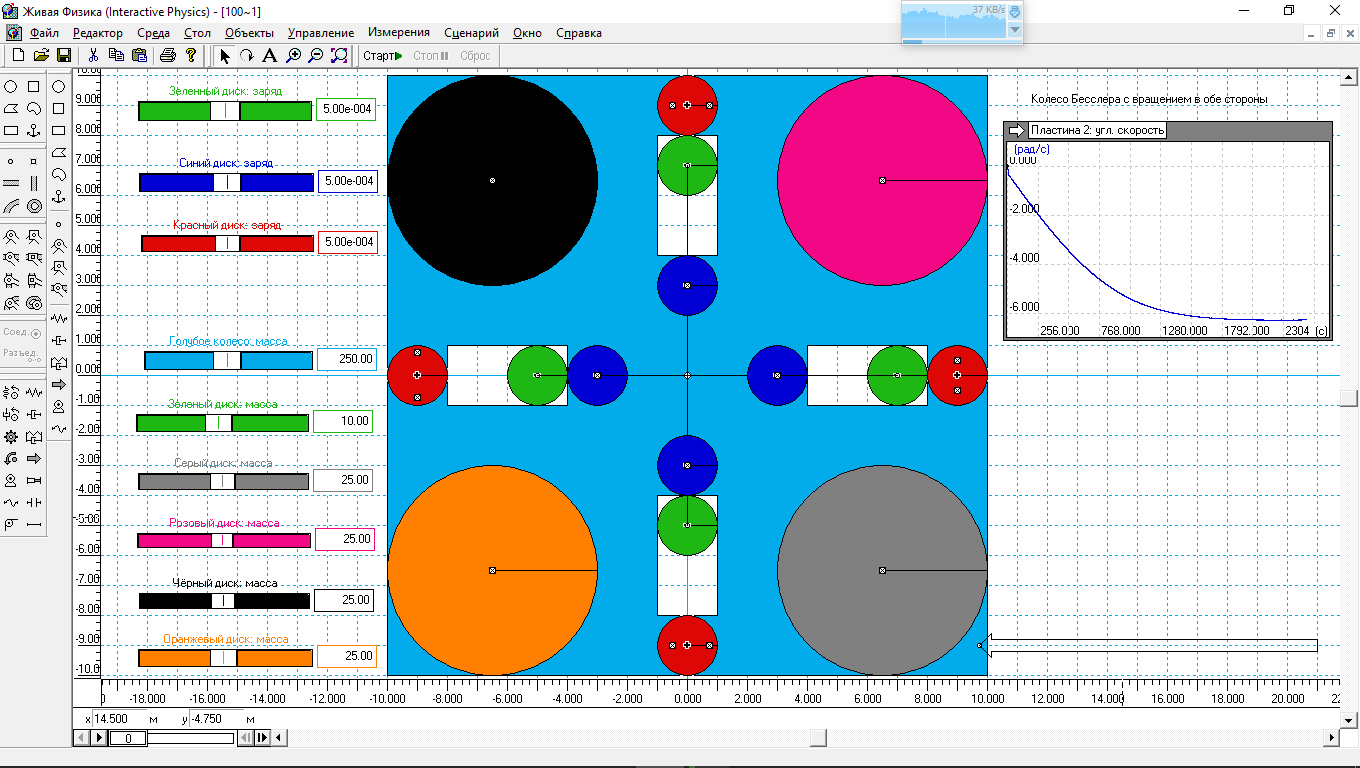
Рис.2. Результат моделирования колеса с тросами между парными грузами.
Всё в этой модели такое же, как и на рис.1. Но дополнительно между зеленными грузами протянуты тросы. Результат моделирования отражает индикатор справа от модели. На этот раз предельная угловая скорость оказалась равной примерно 6.5 рад/с. Это в два раза больше, чем в первой модели.
Значит, использование тросов позволяет поднять мощность гравитационного колеса в два раза. Что крайне важно, если мы будем использовать такое колесо в качестве генератора энергии.
И тут надо вспомнить, что в конструкции своего колеса Бесслер, со слов его покровителя, использовал пружины, тросы и рычаги. Насчет пружин и рычагов пока у меня соображений четких нет, а вот с тросами разобраться удалось. Вместо рычагов в колесе вполне могли использоваться направляющие для грузов. И пока неясно, как они были устроены, так как по всем канонам они должны были бы опираться на «землю». Но этого в описании колеса современниками Бесслера нет. Но внутри колеса мог бы находиться массивный, вертикально висящий маятник. От его направляющих и могли бы отталкиваться нижние грузы из 4-х пар, связанных тросами. Ведь достаточно нижнему, спаренному тросом, грузу чуть-чуть «подпрыгнуть» вверх, как его тут же подхватит и потянет вверх за связывающий их трос второй груз. Потянет, потому что верхний груз будет находиться под действие центробежной силы, а трос, при опоре нижнего груза на направляющую, временно ослабнет (провиснет).
О возможной конструкции массивного маятника и форме направляющих мы обсудим ниже, а пока посмотрим, как влияет на предельную угловую скорость уменьшение массы подвижных грузов. А заодно и масс всех других элементов, за исключением массы одного большого углового диска оранжевого цвета, масса которого установлена в 50 кг. Масса зелёных дисков равна 1 кг, у прочих дисков масса тоже равна 1 кг, масса голубого квадратного колеса равна 10 кг. Фактически, таким способом мы получили в свое распоряжение модель маятника со странным расположением зеленных грузов, обеспечивающих параметрический резонанс по формуле (1).
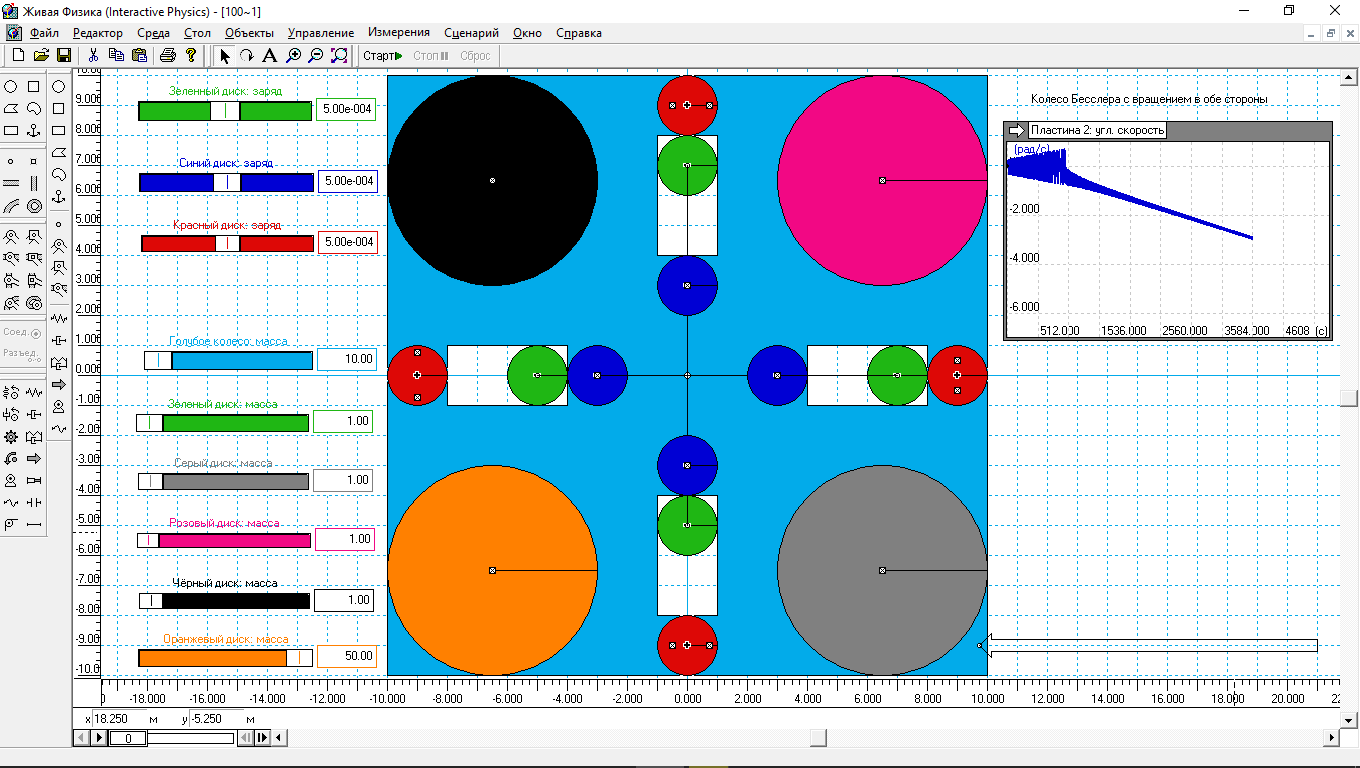
Рис.3. Динамическое превращение маятника в колесо.
На индикаторе отражён результат моделирования поведения такого маятника. Прекрасно видно, что в течение 750 с маятник вел себя как маятник, амплитуда колебаний которого постоянно росла. Затем маятник превратился в колесо. Угловая скорость этого колеса росла по линейному закону, и, одновременно, биения угловой скорости по мере раскрутки этого колеса, уменьшались. Это хороший признак. Эксперимент программа завершила сама из-за достижения внутреннего предела. 4000 с, почти 70 мин – это достаточно большой интервал времени, чтобы в результате моделирования можно составить полное представление о поведение модели. Но по виду графика можно предположить, что угловая скорость будет нарастать и дальше. Не удалось подтвердить, что угловая скорость такого колеса могла бы превысить 6-7 рад/с.
Получается, что тот механизм перемещения грузов, который я назвал именем Бесслера, больше подходит для его маятника, который легко превращается в параметрический. А вот его колесо, похоже, вращалось благодаря тому, что в нижней точке колеса груз поднимался от периферии ближе к оси колеса, а парный ему груз благодаря этому и центробежной силе приближался к краю колеса, поднимая при этом парный ему «нижний» груз. Фиксаторы, возможно, были не нужны, так как грузы могли в некоторых пределах угловой скорости колеса (частоты) четко фиксироваться у края колеса центробежной силой. А чтобы грузы при вращении колеса не падали, они к краю колеса могли фиксироваться пружинами. Но при вращении колеса, грузы, подходящие к нижней точке колеса, получали удар от направляющей. Это обеспечивало более плотное «прилегание» к краю колеса верхнего парного груза. И поэтому, при вращении по часовой стрелке, в левой половине колеса грузы оказывались ближе к оси колеса, а в правой половине – дальше от оси колеса. Это напоминает расположение грузов в колесе Альдо Коста. Только у Альдо Коста гравитоны жестко фиксируются защелками и пружинами, а в колесе Бесслера основной защелкой была центробежная сила.
Висящий в самом низу колеса, но не вращающийся вместе с колесом, груз мог быть такой формы, что колесо могло вращаться одинаково в обе стороны. А это значит, что направляющие, поднимающие нижний груз на короткое время могли быть по форме близки к эллипсу или кривой, которая плавно переходила из окружности в какую-нибудь кривую третьего или более высокого порядка, симметричную относительно вертикали, проходящей через ось колеса. Главное, чтобы груз, проходя по этой направляющей, не заклинивался, еще лучше слегка подпрыгивал (взлетал) вверх. Вот на этом взлёте его мог и подхватывать парный ему и находящийся в верхней точке груз. И за счет центробежной силы поднимался еще выше сам, и поднимал за трос своего «друга».
Думаю, что к массивному полудиску с направляющими Бесслер вынужден был прибегать, чтобы механизм перемещения грузов можно было замаскировать колесом. А в случае удачной продажи своего секрета он бы мог построить более мощное колесо уже с направляющими, опирающимися на «землю», как это сделал Дмитриев, воспользовавшись направляющими, с одной стороны, и обгонными муфтами, с другой стороны. Между прочим, и у него есть вариант с использованием тросов, наряду с использованием обгонных муфт.
Теперь установим у подвижных грузов массу в 10 кг, добавим пружины, и посмотрим, что получим в результате (рис.4).
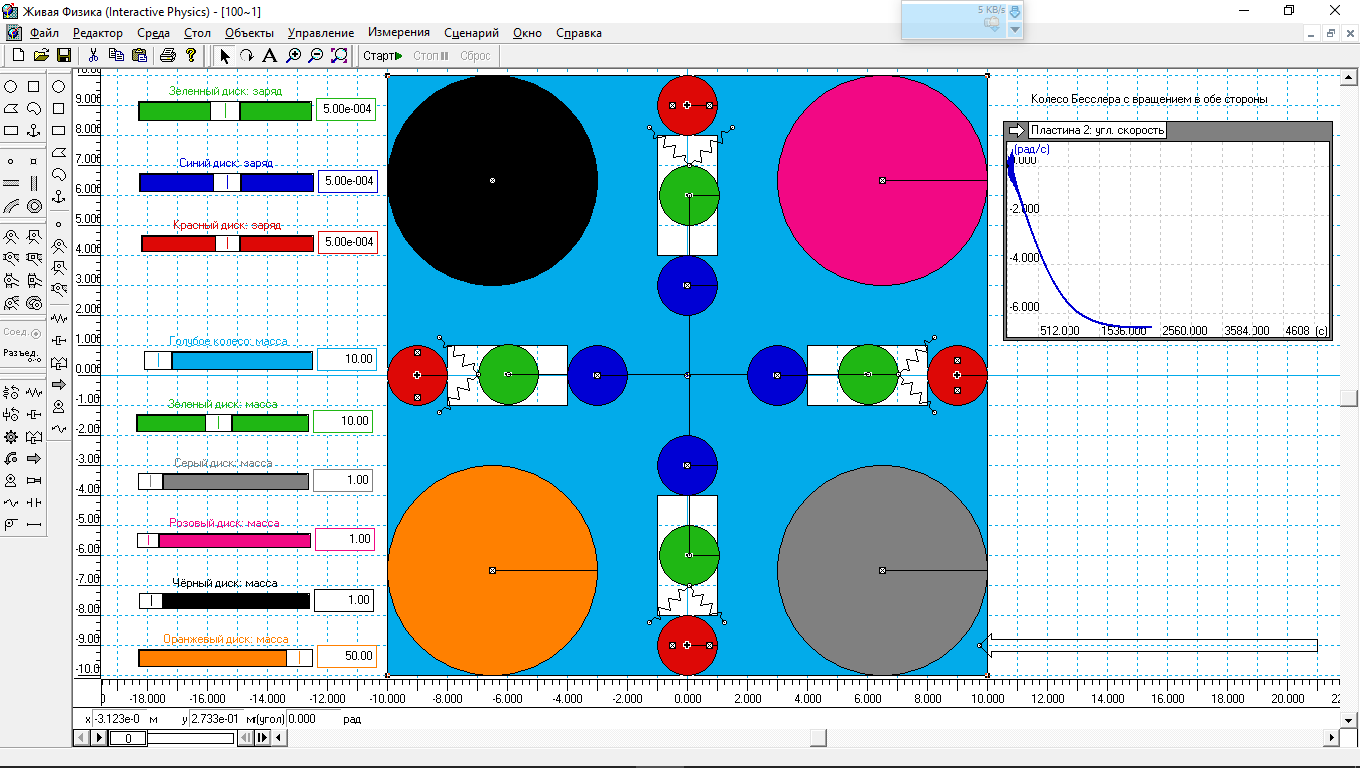
Рис.4. Моделирование маятника с более массивными подвижными грузами.
Получаем максимальную угловую скорость в 6.5 рад/с, даже чуть больше, чем на рис.1. Пружины внесли свою лепту в неравномерность вращение, ибо видно, что кривая немного размазана. Также колесо за более короткий отрезок времени вышло на максимальную мощность, чем на рис. 3. Этому способствовали более тяжелые подвижные грузы.
Данная модель показала, что связка грузов тросами помогает частично уменьшить влияние центробежной силы на максимальную мощность гравитационного колеса с подвижными грузами. Эффект заметный, мощность возрастает в два раза. Но полностью избавиться от влияния центробежной силы на конечную мощность колеса всё же не удалось. И с этим либо придется считаться, либо искать новые способы преодоления ограничений, накладываемых на мощность колеса со стороны центробежной силы.
На рис.5 показан эффект применения пружин как дополнение к тросам. Причем все исходные параметры соответствуют варианту на рис.2, где используются только тросы.
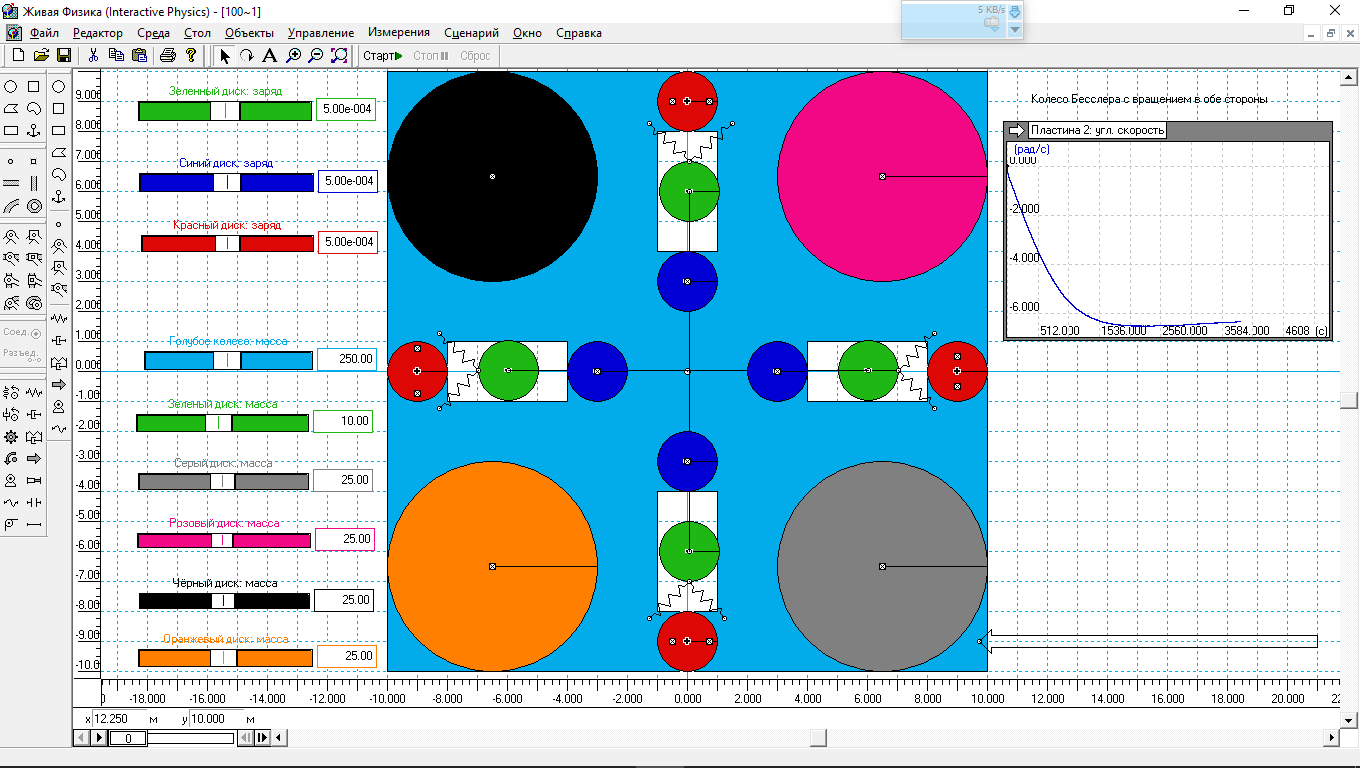
Рис.5. Модель колеса с тросами и пружинами.
Сравнение рис.2 и рис.5 показывает, что конечная мощность колеса практически не изменилась. Да и скорость набора мощности практически осталась прежней. Так что пока на данном этапе выявить пользу от пружин не получилось. Возможно, польза пружин будет оценена в будущих экспериментах с новыми моделями.
Подведём итоги. На данном этапе моделирования гравитационных колёс Бесслера удалось получить подтверждение, что использование тросов (прутов) для связи парных подвижных грузов друг с другом повышает мощность гравитационного колеса. И на основании обнаруженной закономерности удалось сделать предположения о возможном механизме перемещения грузов в колесе Бесслера и высокой вероятности использования тросов, прутов или рычагов в историческом колесе Бесслера. Что касается возможного использования пружин, то это пока оставим на будущее. Надо подумать, как правильно «собрать» подходящую модель.
01.03.2016