Рис.1. Детские качели.
Работая над циклом статей «Величайшая Революция в Механике», я пришел к выводу, что параметрический резонанс – это очень и очень серьёзно. И что, такие конструкции, как трансформатор Тесла, Тестатика, колесо Альдо Коста или бегающий шар Финсруда – это удачные технические устройства, в которых успешно работает параметрический резонанс.
Поэтому было принято решение провести моделирование простейших вариантов параметрического резонанса на базе программы «Живая Физика». «Живая физика» - это 2D симулятор, который успешно применяется в школах на уроках физики, дети познают этот предмет не с помощью скучных формул, схем и статических рисунков, а с помощью, по сути дела, небольших мультфильмов, перед просмотром которых можно настроить параметры всех, участвующих в процессах объектов.
Но, как правило, в прилагаемых к «Живой физике» наборах решений тех или иных физических проблем, нет файлов, в которых моделируется параметрический резонанс, а тем более так называемые «вечные» двигатели. Но любой человек в здравом уме и доброй памяти может сам создать виртуальную конструкцию, похожую на тот или иной «вечный» двигатель и посмотреть, как она будет себя вести после первоначального толчка (силового воздействия). Что я и проделывал неоднократно с разного рода колесами и «Живая физика» помогала мне убедиться, что часто те, кто доказывал невозможность вращения колеса той или иной конструкции, были правы. Но ряд конструкций проверить не удавалось потому, что это требовало создания 3D модели или я просто не знал, как на базе имеющихся инструментов, которыми располагает «Живая физика» создать аналог некоторых механических конструкций.
Для моделирования и проверки механического параметрического резонанса я выбрал простую модель – детские качели, они же весы, они же рычаг третьего рода, у которого плечи и грузы, расположенные на концах, были равными. Но для наглядности привожу рисунок (рис.1)

Эта простая модель была положена в основу более сложных моделей. Но на первом этапе было трудно понять, какой именно параметр и каким образом он должен меняться в зависимости от кинематических характеристик (параметров) качелей. И вначале за параметр, которым следовало бы управлять, была принята масса грузов. На рис 1. грузы эти показаны в виде красных кубиков.
При равенстве масс грузов и плеч рычага (качелей, коромысла) качели будут оставаться в горизонтальном положении сколько угодно долго. Если их немного качнуть, то они покачавшись, за счет трения постепенно остановятся, и скорее всего, опять займут горизонтальное или близкое к горизонтальному положение.
А вот если каким либо образом изменять массу грузов в зависимости от направления движения этих грузов или в зависимости от положения, относительно горизонта, то тут уже сразу нельзя сказать, как будут себя вести эти простые детские качели. Вначале я решил, что надо проверить вариант изменения массы грузов в зависимости от положения их относительно высоты положения оси вращения. Например, когда груз находится ниже оси, то его масса увеличивается, а когда выше – уменьшается. Моделирование показало, что параметрический резонанс при таких допущениях получить не удается.
Тогда чисто интуитивно родилась идея, что масса грузов должна зависеть от направления движения грузов относительно вертикальной оси координат. Когда скорость движения груза по вертикали положительна (направлена вверх), то масса груза должна уменьшаться. Если скорость движения груза по вертикали отрицательна (направлена вниз), то масса груза должна уменьшаться.
Сказано – сделано. Была разработана простая модель, результат моделирования показан на рис.2.
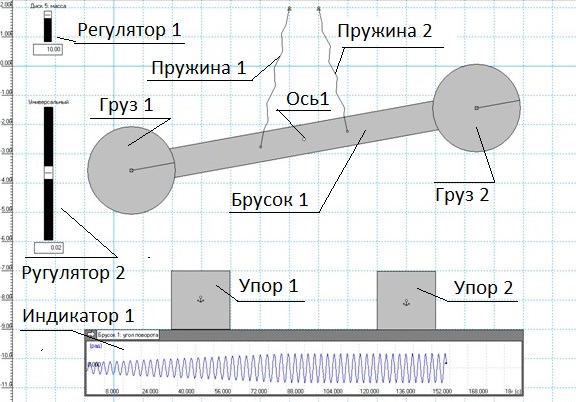
Основная часть массы грузов Груз 1 и Груз 2 задается регулятором 1. В данном случае видно, что масса эта равна 10 кг. Регулятор 2 задает относительное уменьшение груза в при его движении вверх. В параметр МАССА обоих грузов была введена простая формула:
IF(Body[n].v.y>0, Input[1]*(1-Input[2]), Input[1]), где
Body[n] – это левый или правый груз, в зависимости от значения n – порядкового номера тела, который устанавливается системой автоматически. Чтобы его узнать, достаточно выделить объект на столе программы и выбрать в меню свойства. В самом верхнем окошечке будет показано имя объекта – Body[n].
Body[n].v.y – это скорость “v” объекта Body[n] вдоль вертикальной оси “у”.
Input[1] – значение на регуляторе 1
Input[2] – значение на регуляторе 2.
В модель введены пружины 1 и 2, а также упоры 1 и 2. Их назначение – стабилизировать мощность и амплитуду колебаний. Без пружин и упоров качели с первого же оборота начинали вращаться вокруг оси 1.
На Индикаторе 1 выводился угол поворота для бруска 1 – это само коромысло, на концах которого расположены грузы 1 и 2.
Индикатор 1 четко регистрирует, что качели после двух-трех десятков циклов в зависимости от жесткости пружин выходят на максимальную амплитуду и далее уже без остановки будут колебаться, пока не разрушатся от времени и усталости материалов, из которых они будут сделаны.
Остается подумать над тем, как управлять массами грузов. Если массы сделать из твердого вещества, то изменять массы трудно, практически невозможно. Но если в качестве массы использовать жидкость, а оболочку груза (емкости) сделать упругой, то для изменения массы грузов надо будет подумать над механизмом закачки жидкости в емкость или откачки жидкости из емкости. Поднимается груз (емкость с жидкостью) вверх – часть жидкости откачивается в емкость, расположенную вне качелей. Если груз на качелях идет вниз, то ранее откаченная жидкость возвращается обратно в емкость на качелях.
Жидкость можно откачивать и накачивать отдельным насосом, а можно качели сконструировать так, что этот насос будут составной частью качелей. И тогда качели сами будут откачивать и закачивать жидкость в грузы (упругие емкости) на концах качелей. Получим своеобразный пожарный насос, который будет сам себя раскачивать. Заодно и воду качать. А можно такую качалку и нефть научить качать. Красота!
После получения первых результатов пришла идея нагрузить параметрические детские качели на массивный маховик (рис.3)
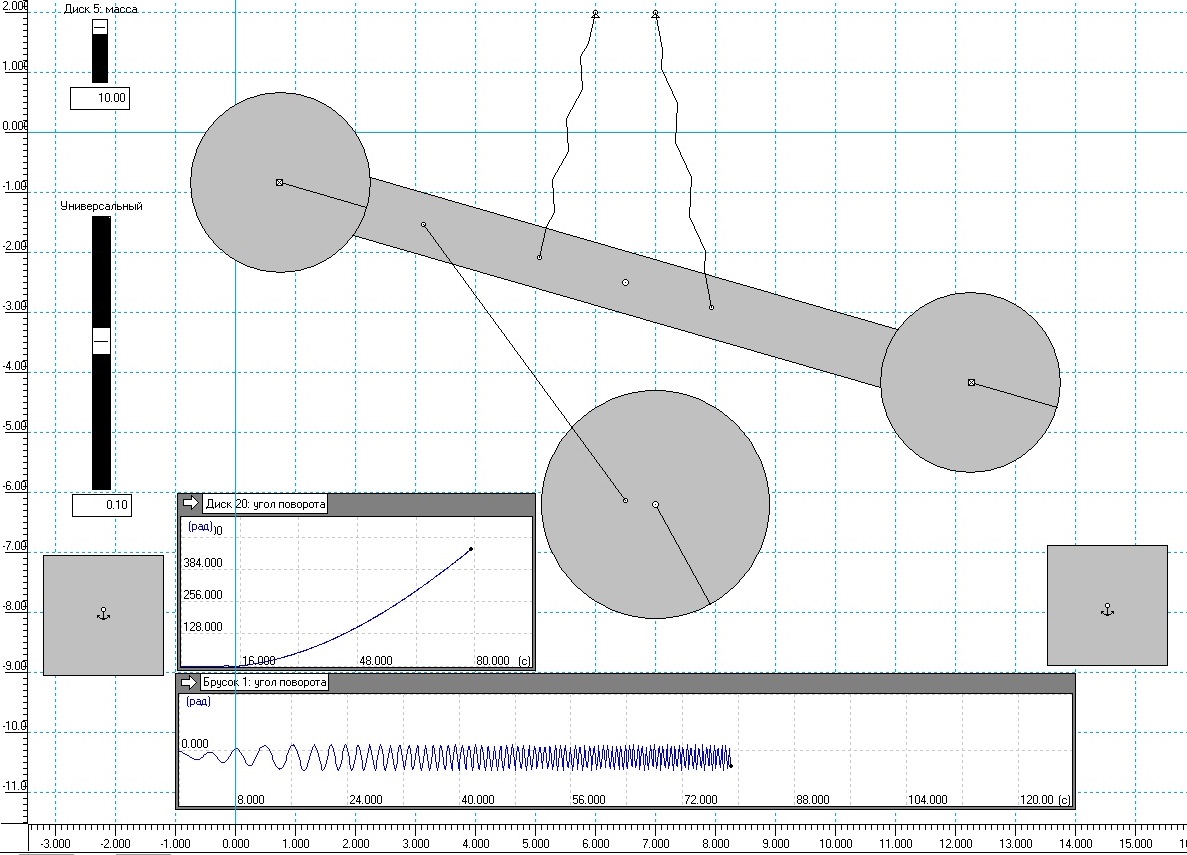
В данном варианте сам маховик ограничивает амплитуду колебаний детских параметрических качелей. На рис.3. можно видеть, как меняется со временем частота колебаний системы. Маховик постепенно увеличивает угловую скорость вращения. И со временем, на рисунке не показано, система идет в разнос и разрушается. Но это без нагрузки. С постоянной нагрузкой поведение системы, возможно, будет иным. Но возможность выхода системы на опасный режим заставило меня подумать о том, как простым способом стабилизировать частоту вращения маховика. И тут вспомнилось колесо Орфира с его двумя большими маятниками.
Поэтому пришлось качели дополнить массивным грузом снизу, как на рис. 4.
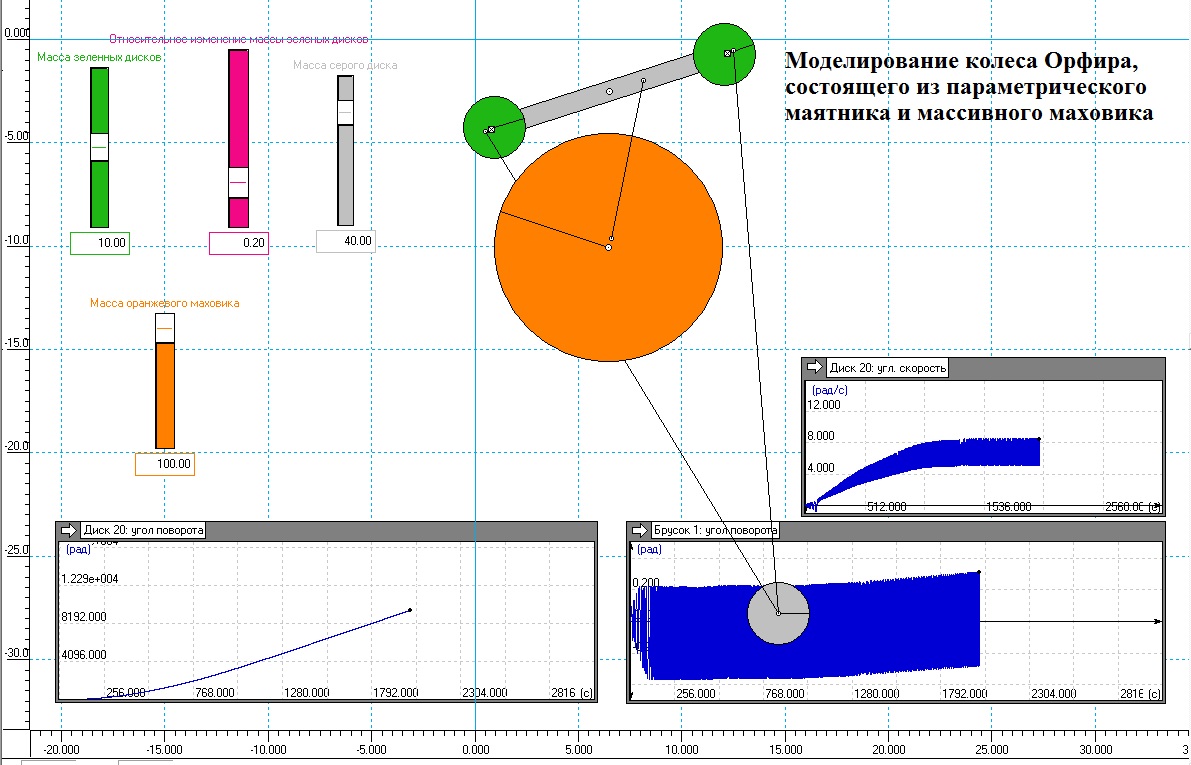
На рисунке прекрасно видно, что добавление к качелям с зелеными грузами на длинных штырях массивного (серого) груза в 40 кг стабилизировало амплитуду колебаний качелей и частоту вращения оранжевого маховика в 100 кг.
Вот теперь и думай, а не был ли секрет колеса Орфириуса скрыт в его массивных маятниках. Орфир, как опытный часовых дел мастер, прекрасно разбирался в маятниках. Поэтому он мог любой маятник превратить в параметрический маятник, используя систему свободно перемещающихся грузов, пружин, прочных шелковых шнуров и прочей фурнитуры.
Действительно, вот фронтальный вид колеса Орфира (рис.5)
У этого колеса 2 массивных маятника. Один спереди, и такой же сзади. Верхнее коромысло с двумя шарообразными грузами можно попробовать превратить в параметрическое устройство, если трубки, соединяющие грузы на горизонтальной перекладине с массивным грузом внизу, превратить в сообщающие сосуды. А сами трубки наполнить водой или ртутью. Шарообразные грузы сделать полыми и соединить с трубами. Тогда при колебаниях маятника тот груз, который будет опускаться, начнет наполняться водой (ртутью), масса его начнет увеличиваться, если шарообразный груз будет подниматься, то вода (ртуть) по трубам будет перетекать в другой груз, а, значит, масса груза будет уменьшаться (при одновременном увеличении массы противоположного груза). А это как раз необходимое условие для параметрического резонанса.
Так это, или не так, можно проверить только на практике. Но если это так, то маятник Орфира сам по себе способен быть генератором энергии, а колесо, вращаясь через кривошип-шатунный механизм, служило ему ограничителем амплитуды колебаний. И колесо при этом могло быть самой простой конструкции, которую мог повторить самый захудалый плотник.
Манипулировать массой грузов, сделанных, например, из металла, достаточно трудно. Но можно перемещать часть массы то ближе к центру качелей, то подальше от них. В этом случаем меняется момент инерции, который создается на том или ином конце качелей. Это отражено на рис.6
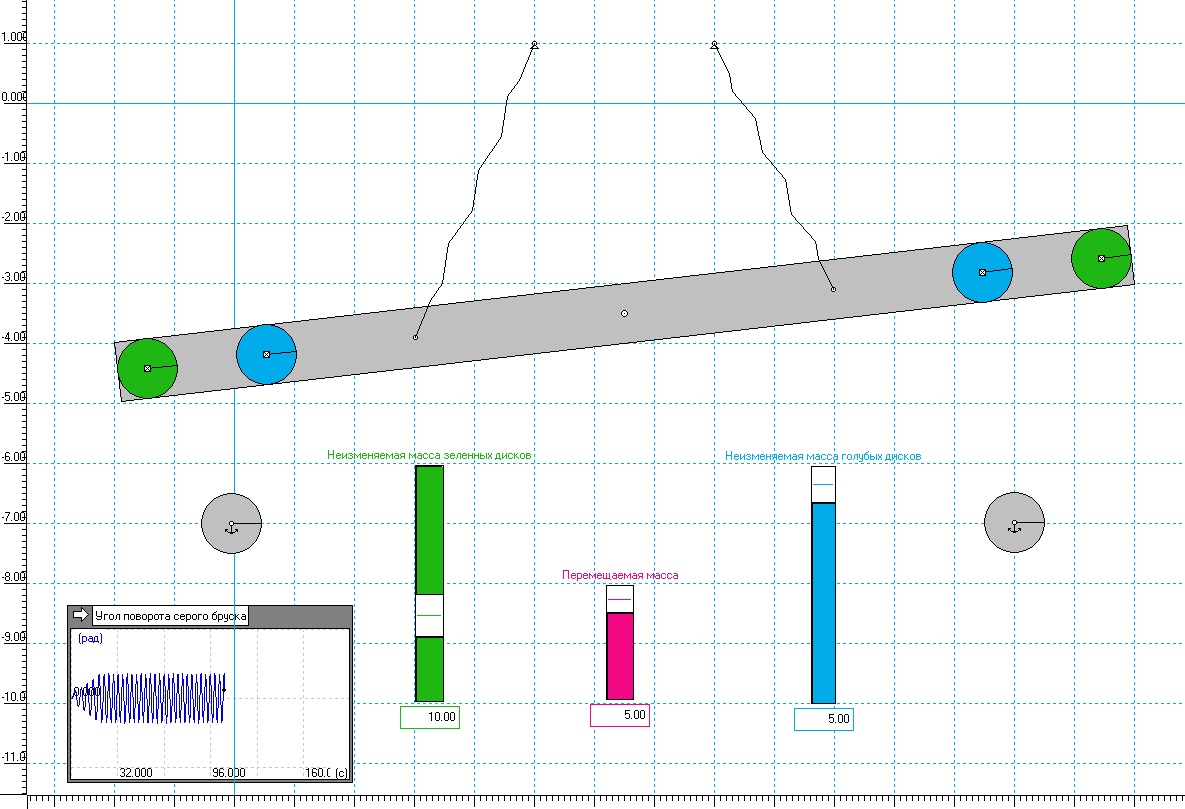
Упоры, серые кружки, в данной модели установлены потому, что без них коромысло с первого же оборота начинает вращаться вокруг оси. Зеленый регулятор задает начальную массу зеленого груза, синий – синего, а красный регулятор определяет массу, которая перемещается от зеленого груза к синему по тому же алгоритму, который описан в самом начале статьи.
Когда зеленый груз идет вверх, то его масса, задаваемая зеленым регулятором, уменьшается на величину, которая задается красным регулятором, а одновременно увеличивается на эту величину масса синего груза. Если зеленый груз идет вниз, то его масса возвращается к величине, которая задается зеленым регулятором, а масса синего груза также возвращается к массе, задаваемой синим регулятором. В результате момент инерции правого плеча рычага (коромысла) всегда больше, чем слева, хотя сумма масс зеленого и синего груза не меняется.
Индикатор показывает, что колебания такого коромысла быстро выходят на максимальную амплитуду, которая определяется положением серых упоров. Используя пружины и металлические массы, можно это реализовать так же, как это сделал в своем колесе Альдо Коста. Но можно в качестве груза использовать жидкость, которую можно перемещать из емкости в емкость с помощью подходящей гидравлики.
Колесо Альдо Коста можно рассматривать как совокупность большого количества детских качелей, грузы которых на концах в нужное время и в нужном месте перемещаются то ближе к центру колеса, то как можно дальше к периферии. Когда его гравитон идет вверх, то масса перемещается ближе к центру колеса, а когда гравитон идет вниз, то его масса смещается подальше от центра колеса. Работает тот же алгоритм, который интуитивно пришел мне в голову. А это означает, что любое гравитационное колесо можно считать параметрической системой и проектировать его как параметрическую систему. И только в этом случае колесо будет вращаться, став генератором энергии.
Мной также исследовалось несколько моделей, где использовались пружины для перемещения грузов в нужный момент времени и в нужном направлении. Моделирование показало, что и этом случае параметрический резонанс легко реализуется как за счет манипулирования массой грузов, подвешенных на пружинах, так и за счет изменения жесткости пружин.
После анализа поведения моделей, созданных на основе детских качелей пришло время создать модель параметрического маятника (рис.7)

Алгоритм изменения массы красного груза прежний. При движении груза вверх его масса, изначально задаваемая красным регулятором, уменьшается на долю, которая указана на синем регулятор – Input[1]*(1-Input[2]). Когда красный груз будет перемещаться вниз, то его масса примет значение, равное тому, что указано на красном регуляторе, в данном случае 20 кг.
Если проследить за динамикой массы красного груза, то в неком фазовом пространстве масса будет описывать некое подобие восьмерки. А вот это уже очень и очень интересно. Ведь восьмерка – это кривая, на определённых участках (точках) которой кривизна может достигать очень больших величин. Рассмотрим схему параметрического маятника, параметром которого является длина нити или штыря, на котором качается груз m (рис.8).
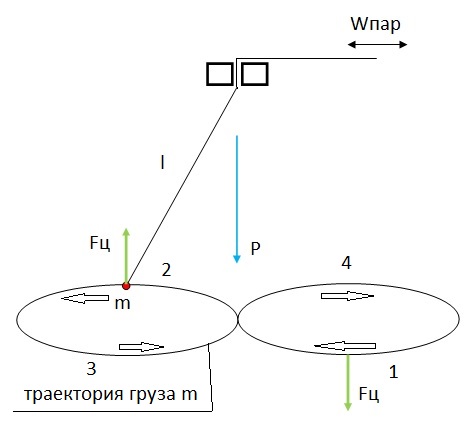
Данная схема поможет нам понять, откуда поступает энергия, которая раскачивает маятник. Принято считать, а может быть грамотные ученые просто не хотят спорить с замшелыми академиками, что энергия в систему вносится механизмом, управляющим длинной нити и задающий режим параметрического резонанса Wпар. Но в этом узле энергия тратится только на трение. А основная энергия поступает по другому каналу.
Любознательный читатель может заметить, что груз маятника m перемещается по траектории, которая похожа на восьмерку. Порядок обхода восьмерки таков – 1 – 2 – 3 – 4. Вначале груз идет по более низкой траектории, затем на участке 2 груз поднимается, на участке 3 груз опять опускается и на участке 4 опять поднимается. Примерно так должны вести себя любители качаться на взрослых качелях - правильно в нужное время приседать и распрямлять свои ноги. Для остановки качелей достаточно делать все наоборот.
В данный момент груз m находится на верхнем участке левой части восьмерки. Это означает, что на груз m действует сила тяжести P, направленная вниз, и центробежная сила Fц, которая направлена на этом участке траектории вверх. Груз перейдет на нижний участок траектории, то сила тяжести по-прежнему будет направлена вниз, а центробежная сила изменит направление, будет тянуть груз вниз.
Для параметрического резонанса следует настроить систему так, чтобы груз из крайних положений всегда двигался по более низким участкам траектории, а от центра к крайним положениям двигался по более высоким участкам траектории. В этом случае поднимать и опускать груз будет центробежная сила, а оператор, управляющий длиной нити (штыря), уже не будет практически на этот процесс тратить энергию. В этом случае кинетическая энергия в системе накапливается, и маятник будет раскачиваться, в противном случае она будет рассеиваться, и колебания маятника быстро затухнут.
Итак, видно, что когда груз из крайнего правого положения движется к центру, а затем от центра к противоположному краю, то он фактически проходит через две зоны, потенциальные поля в которых различны. Вначале проходится поле с высоким потенциалом, так как там сила тяжести складывается с силой центробежной, а затем тело движется уже в поле, где потенциал слабее, так как там из силы гравитации вычитается сила центробежная. В результате, тело, проходя поле с высоким потенциалом, накапливает в себе излишек энергии, который при переходе в потенциальное поле со слабым потенциалом, конвертируется в увеличение кинетической энергии. Когда груз идет из крайнего левого положения к крайнему правому положению процесс повторяется. Теперь потенциальные поля меняются местами, и поэтому груз к крайнему правому положения придет с очередной добавкой кинетической энергии, а, значит, отклонится на больший угол. И так до тех пор, пока маятник не начнет вращаться вокруг оси, либо трение или нагрузка не ограничит его амплитуду. Либо начнут сказываться некие нелинейные эффекты, которые проявили себя в маятнике Орфира.
Если развернуть траекторию груза параметрического маятника на плоскости, то получим череду полос из потенциальных полей, каждая из которых будет разгонять массу m. Если мы развернем траекторию обычного математического маятника, то обнаружим, что полосы, разгоняющие груз будут чередоваться с полосами силовых полей, где груз маятника будет с такой же силой тормозиться, что при наличии трения приведет к остановке маятника. У параметрического маятника, которому дополнительную энергию будут поставлять центробежные силы, меняя свое направление от полосы к полосе, при преодолении трения при начальном толчке колебания уже не остановятся никогда, или по крайней мере до тех пор, пока не разрушится нить или сама масса.
Можно сделать некоторые выводы, что энергию параметрическому маятнику поставляют центробежные силы, которые возникают на участках траектории, по которой перемещается груз маятника. Эта траектория похожа на восьмерку, еще более она похожа на лемнискату. И теперь самое время вспомнить, что именно такие траектории характерны для маятника Капицы и Челомея, а также по такой траектории перемещаются крылья насекомых и птиц при быстром машущем полете. Половинку лемнискаты, слегка деформированную, описывает груз в умножителе силы Фернандо Сиксто Солано. Так что все это заставляет по-новому посмотреть на роль центробежных сил. И их значение в проявлении уже известных физических явлений, которые пока еще списываются на «нечистую» силу или происки лжеученых.
Итак, с механическим параметрическим резонансом стало все более или менее ясно. Анализ работы таких колес, как колеса Альдо Коста или колеса Дмитриева, показывает, что в них тоже работает параметрический резонанс, только он сразу в глаза не бросается, но каждый гравитационный элемент работает по обнаруженному мной принципу. При подъеме элемента вверх его масса (момент инерции, момент силы, удаленность от центра колеса) принудительно уменьшается. Когда элемент идет вниз, то его масса (момент инерции, момент силы, удаленность от центра колеса) принудительно увеличивается. Сделать это можно десятками и сотнями способами. И уже многие изобретатели построили свои конструкции. Дело за малым – чтобы эти конструкции признала официальная наука.
К сожалению, официальная наука этого делать не хочет. И тут дело может упираться как в невежество наших академиков, так и в то, что исследования по параметрическому резонансу засекречены государствами, поэтому ученым просто запрещено обсуждать это в широкой печати. Думаю, что они могли получить от силовых органов установку давить всех, кто посмеет заняться постройкой «вечных» двигателей. А особо ретивых и плодовитых – объявлять лжеучеными. Только правду утаить нельзя.
От механического резонанса мы можем плавно прейти к резонансу в электротехнических контурах, состоящих из индуктивности L, ёмкости C и сопротивления R. Нет смысла приводить тут схему контура, так как контур может быть последовательным или параллельным. Дело в другом. Важно понять, как мы должны изменять индуктивность (ёмкость) в зависимости от изменения силы тока, протекающего через индуктивность (напряжения на обкладках конденсатора).
Проанализируем опять механический параметрический резонанс. Масса груза уменьшается при увеличении его потенциальной энергии и увеличивается при уменьшении потенциальной энергии. В тех точках, в тех моментах времени, которые отделяют подъем и спад потенциальной энергии, первая производная от потенциальной энергии по времени равна нулю. Если продолжать в этом направлении, то получаем, что в критических «точках» произведение скорости на ускорение равно нулю – v*v’=0. Таких точек в механической системе может быть как 2, так и 4. Всё зависит от того, как ведет себя механическая система в потенциальном поле. Например, для детских качелей таких точек 2, а вот у маятника таких точек 4.
Так и в электрических колебательных контурах. Если колебания релаксационные или в виде положительных импульсов, то точек, моментов времени, в которых необходимо переключать выбранный энергоемкий параметр, будет 2, ну а если колебания в контуре гармонические, или близкие к этому, то таких точек будет уже 4. Например, пусть нам надо управлять индуктивностью, колебания гармонические. Тогда моменты времени, в которых надо переключать индуктивность с большой на малую и наоборот, будут определяться простым условием – в этих точках сила тока, либо скорость изменения силы тока будут равны нулю. Причем надо обеспечить с самого начала уменьшение индуктивности при увеличении силы тока в этой индуктивности. Ну, а далее процесс уже пойдет автоматом, если в критических точках менять индуктивность с малой на большую, а затем с большой на малую, неизменно соблюдая этот порядок все время. Так же надо работать с емкостью, если она выбрана в качестве параметра. Это и будет резонансом в резонансе.
Конечно, эффекты, которые открылись мне при моделировании параметрического резонанса с помощью программы «Живая физика», нуждаются в дополнительном изучении. Но даже этих фактов уже достаточно, чтобы сделать очень полезные выводы – параметрический резонанс – это очень и очень серьезно. На это указывает и тот факт, что в Интернете крайне мало статей о параметрическом резонансе. А еще меньше статей о конкретных устройствах, в которых параметрический резонанс поставлен на службу человеку. Значит, эта тема засекречена, так что изобретателям надо быть крайне осторожными, а не носится со своими заявками на патент по всему миру, а идти сразу, например, в ФСБ. Думаю, что эта статья русского дилетанта поможет тем, кто ищет свободную энергию.
Приложение:
14.07.2013