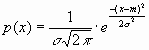Несколько шагов в интересную сторону… (часть 1)
Сергей А. Алферов
Эта тема возникла более года назад. Вдруг стали совпадать «картинки» отдельных самостоятельных исследований в разных предметных областях. Это были итоговые графики распределений ресурсов в осях, задающих доли общей суммы (общего целого). Конечно, сразу возникло понимание важности соединения этих отдельных результатов, тем более, что они трактовались авторами по-своему. И так как содержание темы превышало мои возможности (в глубине познаний и свободном времени), я попробовал переадресовать задачу... Могу в очередной раз подтвердить, что «инициатива наказуема» изначально. Не обессудьте, здесь я попытаюсь изложить эту тему.
1
В начале мне придется повторить исходное из текста «Гармоничное распределение доходов и Золотая пропорция» (http://www.trinitas.ru/rus/doc/0232/009a/02320025.htm).
…интересны критерии, признаки «благосостоящего общества». Фундаментальные критерии его находятся в духовной сфере. Но есть критерии социальной жизни, критерии «на поверхности», являющиеся, тем не менее, точными индикаторами состояния и перспектив общества. По ним и должен осуществляться федеральный мониторинг социального здоровья общества...
Причины, которые приводят к конкретным распределениям, могут быть разные… Здесь нам важен показательный индикатор, через который можно предвидеть социальные потрясения или благополучие, предвидеть изменение качества жизни.
Индикаторы устойчивости и эффективности социума связаны с пропорциями распределения зарплаты и собственности... Зарплата, как основной элемент в суммовом потребительском обороте, достаточно четко интегрирует процессы (прямые и обратные связи), позволяет анализировать экономические и социальные последствия установившихся пропорций и прогнозировать «макроэкономическое поведение». Важен первый элемент культуры распределения в обществе – распределение зарплаты…
…Существуют кривые распределения доходов, которые задают границы эффективности. Исходные данные, зависимости и соответствующие им кривые – «эмпирические». Границы/кривые – имеют разное значение.
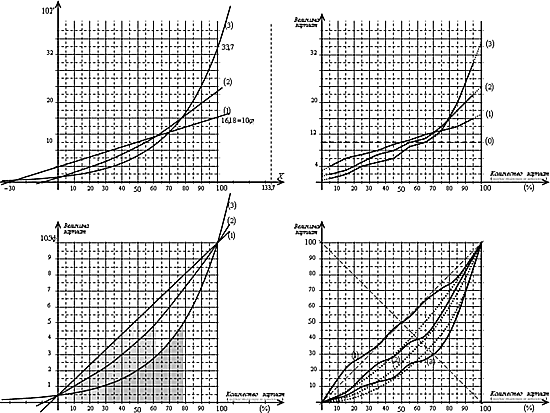
Сначала – о системе координат. Получилось так, что форму графического представления данных продиктовали сами цели исследования. Полученные графики идентифицировались для себя, как «графики распределения в суммовых относительных величинах». Несмотря на то, что через 3 года я узнал, что эта форма имеет название «диаграмма Лоренца», старая идентификация по своей содержательности осталась мне близкой. Дальше мы увидим, что это представление и сами функции имеют ещё одну идентификацию, наиболее точно позиционирующую ее место в существующей методологии знания.
Итак, по оси X откладывается количество зарплат нарастающим итогом (в %).
По оси Y — суммовая величина всех зарплат от меньшей до данного значения Х нарастающим итогом (в %).
1-ая кривая, самая верхняя – кривая уравнительности. Выход реальной кривой распределения за нее вверх («выпрямление») приводит к неэффективной уравнительности. 2-я кривая – кривая «допустимой дифференциации доходов», кривая «социальной эффективности». Между 1-й и 2-й кривыми образуется коридор нормальных распределений, коридор «социальной эффективности». Кривые распределения доходов в европейских развитых странах оказались по факту развития этих стран именно в этом коридоре.
3-я кривая – кривая «опасного распределения доходов». Она является кривой опасности, кривой деструктивных процессов в социуме. Соответственно, коридор между 2-й и 3-й кривыми – это коридор опасности, коридор нарастающей социальной дисгармонии, коридор нарастающей «социальной неэффективности».
Как видим на нижнем рисунке, в координатной сетке «суммовых относительных величин» имеется узкий коридор социальной эффективности между первой и второй кривыми (в ~10% на участке 40% — 90% от низа зарплат).
Эти кривые имеют эмпирический характер, но они точно аппроксимируются формульными зависимостями. Типы этих зависимостей по своим математическим свойствам очень характерны этим кривым.
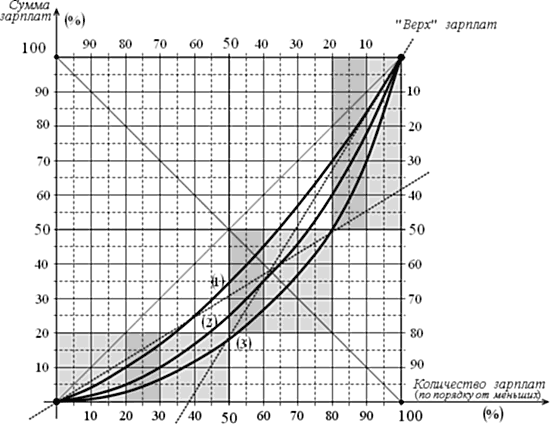
Соотношения
1-ой кривой «А» описываются формулой: ![]() .
.
Вторая кривая «А» описывается средней линией
между
параболой y=0,01x2 и показательной функцией ![]() .
.
После 2-ой кривой (ниже) вообще невозможно аппроксимировать параболой!
Третья
кривая «А»
описывается показательной функцией: ![]() .
.
(Только напомню: 2=1,618…, =(2- 1)0,5, 1=0,618…)
Ограниченные 3-мя кривыми два коридора распределений имеют физический (предметный) и математический смысл:
- 1-ый (верхний) коридор – коридор «нормальных распределений доходов» является «параболическим» коридором,
- 2-ой (нижний) коридор – коридор «нарастающей социальной дисгармонии» является «показательным» коридором.
Итак, эти кривые, имеющие еще смыслы ограничения в «налоговых линейках» (см. полный текст) и называемые «Золотые кривые», обозначаются, как «А»-кривые. Полученные от них дифференцированием кривые распределения конкретных значений величин, называются «В»-кривые.
Как видим, Золотые А-кривые не симметричны относительно диагонали (100,100). «Эксцентриситет несимметричности» (или выпуклость) расположен у них в нижней части (х<50%). Понимание смысла места выпуклости нам пригодится дальше. Поэтому приведем выдержку из заключения «опорного текста», содержащего описание параметров, по которым можно определить и выразить смещение «эксцентриситета кривизны» в неких опытных кривых распределения относительно «базовых кривых» (там это были кривые семейства А-1, А-2, А-3, но это не важно).
Кривизна (если хотите – «степень изогнутости») кривых рассматривается относительно диагонали абсолютной уравнительности (y=x). При этом стандартное семейство кривых «А» задает стандартный «эксцентриситет кривизны» для других подобных кривых. То есть мы хотим рассмотреть случаи, когда новая опытная кривая пересекает «семейство А-кривых», или в общем случае, когда она относительно «семейства кривых нормального эксцентриситета» проходит по разному на начальном и конечном участках: круче на одном и положе на другом. «Круче» — то есть «выпучиваясь» ниже за кривые нормального распределения кривизны.
Прежде всего – что означает такое поведение?
Более кривая линия (в целом, или на каком то участке) отражает менее уравнительное распределение, или, по другому, – распределение доходов с более быстрым нарастанием по мере их роста. Если сравнить начальный (до X=50%) и конечный участки, то, разумеется, более быстрый темп нарастания зарплаты в социуме целесообразен как раз на начальном участке. Что и отразилось в изображении (и формулах) кривых: их максимумы относительно диагонали «y=x» находятся на этой половине. Мы говорим о «нормальном эксцентриситете кривизны» в зоне X<50%!
Если относительно какой-то стандартной А-кривой новое опытное распределение проходит на начальном участке выше, а потом, пересекая стандарт-кривую, проходит ниже, то в общей сумме зарплаты доля меньших зарплат увеличивается, и при этом эта доля распределяется равномернее. Вообще-то, стандарт-кривые в рамках общей задачи определения гармоничного распределения доходов оптимальны по форме: по соотношению темпов возрастания доходов, по изменению темпа. Наибольшую крутизну у них имеют начальные участки. Наибольшую крутизну относительно конечного участка имеет 2-ая кривая, это видно на рисунке по приближению в начале 2-кривой к 3-кривой. То есть 2-кривая дает «послабление» доле больших зарплат, «требуя» при этом быстрого нарастания в меньших зарплатах.
2
В апреле этого года на сайте «Академия тринитаризма» была опубликована статья Г. Я. Мартыненко «Золотое сечение в нумерологии текста» (http://www.trinitas.ru/rus/doc/0232/004a/02321035.htm). Приведем выдержки и из нее.
«Итоговые турнирные таблицы футбольных чемпионатов, организованных по круговой системе, отражают результаты длительной турнирной борьбы. Для каждой команды эти результаты фиксируются в виде числа побед, ничьих и поражений, за которые начисляется определенное число очков.
Каждая из таких таблиц может рассматриваться как убывающее ранговое распределение, в котором в качестве независимой переменной выступает номер места, занятого командой в данном чемпионате, т. е. ранг, а в качестве зависимой переменной — число набранных очков.
Установлено, что такие таблицы для стран с нормальным, усредненным уровнем развития футбола обладают определенными симметрийными свойствами, а именно:
1. Если турнирную таблицу разделить на две равные половины по оси рангов, то количество очков, набранных командами, относящимися к верхней половине таблицы, тяготеет к золотому числу 0,618, т. е. зеркальной симметрии по оси рангов приблизительно соответствует золотая симметрия по оси очков.
2. И наоборот, если турнирную таблицу разделить на две половины с одинаковым количеством очков, то граничной точке 0,5 будет соответствовать золотое число 0,382 по оси рангов.
3. Золотому числу 0,618 по оси рангов соответствует золотое число 0,736, равное 0,5 + 0,236.»
Вот здесь – стоп. Сделаем комментарий. Если «в турнирной таблице равные половины по оси рангов» — это равные количества команд сверху и снизу по занятым местам, то те же 3 пункта можно сформулировать так:
1. Верхняя половина команд имеет примерно 62% очков от общей суммы очков (от 100%); соответственно, нижняя половина команд ~38% очков.
2. По 50% очков набирают ~38% верхних команд и ~62% нижних.
3. 62% верхних команд набирают ~74% очков.
Ну а теперь дальше.
Соответствие между симметрийными точками по оси рангов и оси очков показаны на рисунке.
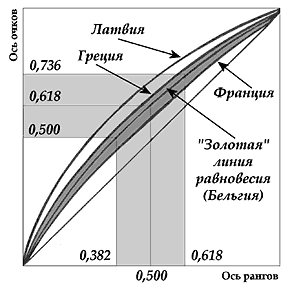
Здесь мы видим основной «золотой полукрест», построенный на основании соответствия чисел зеркальной и золотой симметрии, а также два «полумесяца»: внутренний и внешний. В первом группируются чемпионаты, тяготеющие к гармоничному соотношению очкового багажа лидеров и аутсайдеров. Это соотношение регулируется правилом золотого сечения. Здесь группируются преимущественно крепкие европейские «середняки» (чемпионаты Чехии, России, Португалии и др.). Во втором полумесяце располагаются чемпионаты, сильно отклоняющиеся от нормы в ту или иную сторону: или в сторону выравнивания класса игры между «элитой» и «периферией» (например, чемпионаты Италии, Франции, Англии), или в сторону резкого разрыва в классе между ними (например, чемпионаты Германии, Голландии, Греции).
…В работе на материале футбольных таблиц мы старались показать, что в некоторых случаях распределение активностей между элитарной и периферийной подмножествами команд, образующих лигу, регулируется симметрийными отношениями по оси рангов и оси «заработанных» в ходе чемпионата очков на основе правила золотого сечения (см. раздел 5).
…Резюмируя сказанное, отметим, что во всех наших иллюстрациях соотношение между новизной и известностью, простотой и сложностью, стандартностью и уникальностью, элитарностью и периферийностью регулируется законом золотого сечения.
Прокомментируем дальше. Как принято, ранги упорядочиваются (нумеруются) от большего (лучшего) и откладываются на оси абсцисс от начала координат. То есть на верхней диаграмме шкала оси «Х» выстроена от большего к меньшему в отличие от диаграммы «шага_1». Совместим эти 2 диаграммы, для чего развернем футбольную диаграмму так, чтобы было следующее значение осей:
«X»: суммарные группы участников, то есть количество участников по нарастающей по порядку от занявших последнее место, в (%),
«Y»: суммарное количество очков, полученное каждой «суммарной группой»» оси «X», в (%). То есть будем строить по пунктам предыдущего комментария.
Результат внизу, но рассматривать его придирчиво не стоит. Я вообще думал не приводить его, так как есть вопросы к графическому исполнению футбольной диаграммы. (Увы, адресов автора Г.Я.Мартыненко я так и не смог найти.) Но чтобы была ясность, о чем идет речь, я решил все же показать результат совмещения.

Видно, как нечетко приходят линии футбольной диаграммы в начало координат. Возникают сомнения и по поводу места эксцентриситета (ассиметричной выпуклости) футбольных линий; здесь он получился вверху. (А вот если бы наложить диаграммы другими концами, то: а) линия А1, имеющая квадратное уравнение y=0,01 1x (x+100 1), пройдет точно между линиями «Греции» и «Золотой»; б) линия А2 практически совпадет с линией «Латвии».)
А в остальном и в целом смысловое и графическое совпадение главных линий диаграмм интересно…
3
Чтобы не возвращаться к последующему пункту еще раз и увидеть всю его тему сразу, вспомним здесь формулы и образы статистики. Их хорошо можно увидеть на ресурсе Интернет: http://www.nsu.ru/mmf/tvims/chernova/PlotDist.html.
Следующие определения даны на основании материалов Интернет.
|
Распределение … |
Принцип (идея) |
Плотность вероятности |
Примечание |
|
«Нормальное» |
|
|
Стохастические системы |
|
Парето |
|
|
Социальные системы |
|
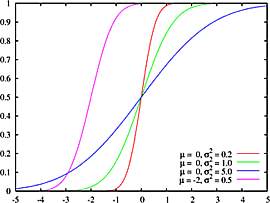
Вейбулла |
|
|
Системы со «слабым звеном». Наличие внешнего управляющего воздействия… b – масштаб, a – параметр формы |
*) Кривая нормального распределения Гаусса (колокол с вершиной (x=0, y=1) и расходящимися краями к «у=0» в x-бесконечностях) есть суперпозиция показательной функции и параболы (отрицательная парабола служит аргументом степени для основания «e»).
**) Эти параметры приводят к наиболее простому виду формулы функции распределения (см. дальше)
***)
Интересно вспомнить здесь 2 красивых интеграла:  и
и 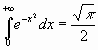 (Пуассона).
(Пуассона).
Плотность распределения вероятности показывает как часто в определенном одинаковом событии появляется случайная величина «x» в некоторой окрестности точки х0.
На
следующих рисунках изображены: слева – функция плотности вероятности p(x),
справа – функция распределения ![]() .
.
Распределение Гаусса
|
|
|
Интересно видеть, в каких формах проявляется закономерность, обнаруженная Парето, а вслед за ним и другими исследователями:
распределение числа граждан и предприятий наиболее развитых государств Европы по величине их доходов «х» ( 2, В.Парето, 1897 г.)
распределение городов по численности в отдельных странах (( 1, Ф.Ауэрбах, 1913 г.; если территория представляет собой целостный экономический район, население n-го по размеру города составляет 1/n числа жителей самого крупного города: Nr = N1/r.)
распределение слов в языке (Эсту, 1916 г.<до Ципфа!>; в языке является константой величина, являющаяся произведением частоты встречаемости слова и его порядкового номера (ранга) в списке слов, упорядоченном по убыванию частоты Nr r C = const.)
распределение биологических родов по численности видов (Д.Уиллис, 1922 г.)
распределение числа научных сотрудников в зависимости от числа опубликованных ими статей ( =2 3, А.Лотка, 1926 г.)
распределение городов по количеству их населения ( 2, Г.Саймон)
распределение различных слов в литературном и разговорном языке (
1,1, Д.Ципф, 1948 г.;
частота использования в естественных языках n-го по списку используемости слова
приблизительно обратно пропорциональна «n»)
распределение документов внутри какой-либо тематической области
(С.Брэдфорд; закономерность концентрации и рассеяния научно-технической
информации)
распределение ученых по числу опубликованных работ (Д.Прайс)
распределение филателистов в зависимости от величины и стоимости их коллекций
распределение вкладчиков г. Москвы по величине их вкладов
распределение количества фирм по группам разной численности
и т.д. (так и хочется спросить «Кто следующий?»)
Саму же общую закономерность популярно называют «закон 80/20» или закон рангового распределения: 20 процентов элементов системы имеют значение на 80 процентов, 20% чего-то (кого-то) дают 80% результата.
В распределении Парето интересно то, что характер (графический вид) верхних закономерностей подобен виду функции плотности вероятностей. То есть плотность распределения Парето подобна характеру взаимосвязи соседних элементов (величин) распределения; или за функцией плотности стоит образ конкретных распределений ресурсов. Но о формализме и «статичности» этого популярного и «раскрученного закона» еще ниже.
Обратим внимание, что в верхнем списке зависимостей по оси «Х» откладываются:
1. ранги объектов измерения (место в списке по порядку от наибольшей измеренной величины),
2. границы групп объектов, ранжированных по измеряемой их характерной величине.
Сами ранги по смыслу также являются группами, количество и границы которых исследователь выбирает сам. Размер ранга исследователь выбирает, как необходимо ему, и этот размер диапазона измеряемой величины часто разный. Исследователь подбирает череду диапазонов для рангов с тем, чтобы получающаяся линия была равномерно (монотонно) изменяющейся. Понятно, что это делает ранги непропорциональными изменению величины. Более того, сами эти диапазоны получают системное значение, и должны становиться неким стандартом для возможности сопоставления однотипных выборок.
Есть только один способ избежать этих проблем (неопределенности): необходимо шкалу делать относительной, приводя любой диапазон «min-max» к 100%. И здесь есть один вопрос: оставлять шкалу такой или делать ее (и соответственно, ортогональную ось и всю координатную сетку) суммарной, то есть нарастающим итогом?...
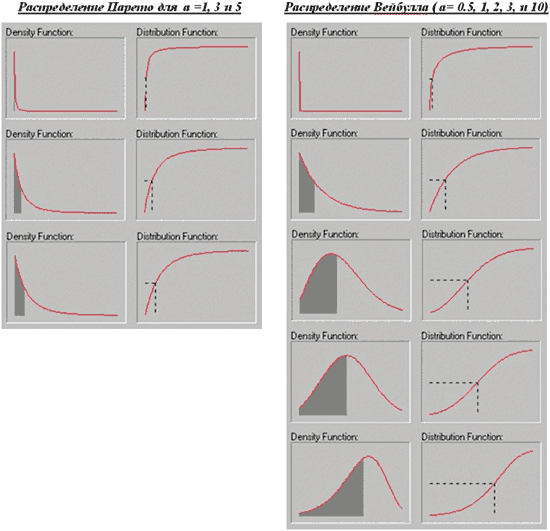
Приведем более четкие графики распределения Парето с Интернет-ресурса «Википедия». В отношении соответствия табличной формуле: здесь k a, и присутствует, задавая сдвиг, множитель (xm)k=1.
|
|
|
Зачем выше приведены диаграммы распределения Вейбулла будет понятно из сопоставления их с соответствующими рисунками следующего «шага».
4
Полтора
года назад прислал мне А.С. Харитонов 2 файла![]() 1.
В них были небольшие статьи сотрудников МИФИ. По ним то и была поставлена
задача этих «шагов». Найти самих авторов через Интернет, как позднее и
Г.Я.Мартыненко, не получилось. Итак.
1.
В них были небольшие статьи сотрудников МИФИ. По ним то и была поставлена
задача этих «шагов». Найти самих авторов через Интернет, как позднее и
Г.Я.Мартыненко, не получилось. Итак.
Матохин В.В. ««Золотое сечение» управленческих решений», журнал «Электроника: наука, технология, бизнес», №3-4, 1997, С. 99-102
Крянев А.В., Матохин В.В., Климанов С.Г. «Статистические функции распределения ресурсов в экономике», МИФИ, 1998
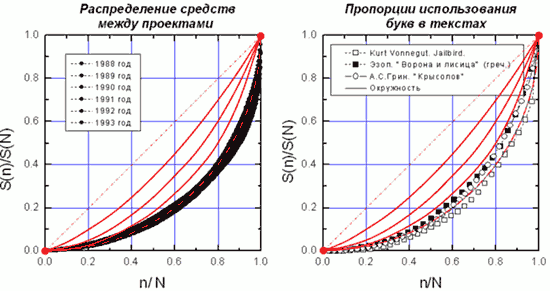
Нижние рисунки – из первого текста. Общая тема видна сразу. Потому то для сравнения и совмещены на них красными линиями «Золотые кривые».
В тексте В.В.Матохина было озвучено явление, был дан анализ разных ситуаций и предложена оптимизация выбора именно по окружности, как принятому эффективному распределению. Текст кончался словами.
«Вы спросите: «Ну и что из этого следует?». Наблюдая окружающий Вас мир, Вы часто удивляетесь порядку и гармонии. Пытаясь познать причину, человек расширяет свои знания, начиная понимать все более и более глубинные уровни взаимосвязи явлений окружающей нас природы. А как же быть с самим человеческим обществом? Почему мы иногда способны договариваться, если все такие разные? Почему какую-либо вещь мы признаем красивой? По-видимому, согласия невозможно было бы достигнуть, если бы в человеческой природе не существовало объективных законов гармонии. Все превратилось бы в хаос. К счастью общие правила все-таки существуют. Возможно, знание таких общих правил позволит скорее сделать еще один шаг к гармонии нашей жизни.»
Во втором тексте (В.В.Матохин и соавторы) был уже дан анализ семейства кривых, где окружность это частный случай при а=2. Общая формула семейства при прохождении кривых через начало координат, как на левом нижнем рисунке: (1 y)a + xa = 1.
Задача была сформулирована так:
На настоящее время уже известно более десяти представлений формулировок статистических функций распределения, связанных с обществом вообще и с экономикой в частности. Многообразие представлений на фоне различной степени общепризнанности каждой из них стимулируют попытку определить вариант, в определенном смысле наилучший для анализа микроэкономического «газа». Сразу оговоримся, что, принимая во внимание изменения во времени исследуемого объекта, речь не идет о попытке свести экономику к идеализированному застывшему состоянию. Речь может идти только о попытке найти такое статистическое распределение, к которому общество постоянно стремится, но никогда в нем продолжительно не находится. В каком-то смысле ситуация подобна маятнику, стремящемуся в процессе колебаний к точке покоя.
Упомянутое многообразие математических представлений статистических распределений заставляет изначально отказаться от еще одной прямой интерполяции исходных данных и предпринять попытку вывести функцию распределения из более общих принципов. Иными словами, исходные данные интегрируются сначала в систему, позволяя уменьшить влияние составных частей, далее выделяется основная компонента, а затем с помощью дифференциального исчисления находится искомая функция распределения. Конечно, такой способ вносит дополнительную погрешность, особенно на этапе аппроксимации. Но с другой стороны, использование предварительного интегрирования исходных данных в систему позволяет проводить анализ распределений как единого статистического ансамбля и предоставляет, как видно будет из дальнейшего, дополнительные возможности по исследованию экономических решений.
Задачу авторов просто можно сформулировать так: найти функцию плотности вероятности, исходя из определенных линий «диаграммы Лоренца». Функции, которые были представлены на последней, были симметричными относительно диагонали «1-1» (то есть некими «базовыми») и назывались «функциями управления ресурсами». Рядом математических преобразований была получена следующая формула функции плотности распределения вероятности:

На нижних рисунках представлены соответствующие графики из 2-го текста.
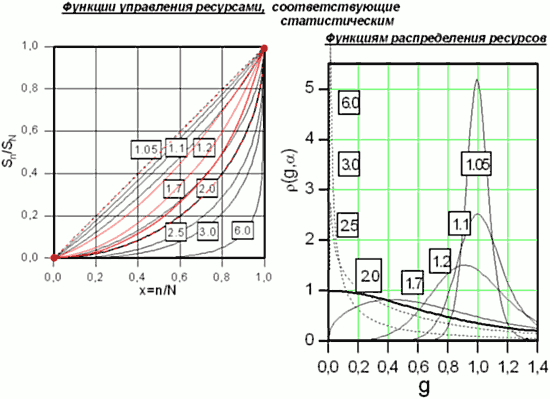
Здесь
![]() это величина ресурса, приведенная к
среднему значению по выборке.
это величина ресурса, приведенная к
среднему значению по выборке.
(Комментарий по поводу этого значения оси абсцисс – смотри дальше.)
В результате были сделаны выводы о «пограничности» линии окружности (а=2) на диаграмме Лоренца « Таким образом, функция управления, которой на плоскости Лоренца соответствует окружность, играет роль границы, разделяющей плотности семейства (g, ) на два класса. Более того (g, 2) — единственная плотность семейства (g, ), >1 принимающая ограниченное ненулевое значение при g=0.» Всё.
Надо здесь сказать, что значение p(0,2)=1 изменяется скачком в начале координат. И вид этой линии на правом верхнем рисунке не соответствует поведению функции возле начала координат. На всем протяжении она практически совпадает с линией «а=1,9» (см. рисунок ниже).
Посмотрите, насколько поведение полученной в МИФИ функции плотности вероятности напоминает поведение в распределении Вейбулла. Только формула сотрудников МИФИ однопараметрическая и без «посторонней» степени над «e».
Полученная формула, мне кажется, это очень интересный результат. И здесь будем называть это распределение «базовым распределением МИФИ».
«Остановки внимания» и выводы из первого просмотра этих двух текстов полтора года назад были следующими.
1. Любопытно, как на последнем рисунке группа Золотых линий «А» встала в пустую область между линиями «а=1,2» и «а=1,7»…
2. Любопытно, как на диаграмме распределения букв в текстах нижняя предельная граница кривых «А» совпадает с верхней предельной границей кривых рисунка…
Распределение букв в текстах на разных языках интересно само по себе, как факт. Можно предположить, что в более богатых языках (более выразительных, с большим количеством букв) распределение будет более пологим. Так и есть: верхняя кривая – русский текст, нижняя – английский.
То, что речь и язык достаточно «эксцентричны», «экспрессивны», выборочны в использовании букв – факт сам по себе интересный. (Как и то, что слово составленное с 1-ой до последней буквы по наибольшей частоте (пропорции) их использования, является как бы наиболее характерным для народа-носителя этого языка; для русского – это «простор» и «простота».)
3. Распределение средств на проекты, действительно, должно быть достаточно неравномерным, чтобы средства не распылялись. Более того, по мере развития проектов, их количество должно уменьшаться, должна происходить концентрация разработок перед практическим внедрением. В этом – специфика в отличие от распределения зарплаты (доходов), как только еще начала процесса социального перераспределения.
4. Насчет «гармоничности» линии окружности (хотя во втором тексте этого так напрямую уже не было. Надо осторожно обобщать все явления во всеобщий Закон вот так абстрактно, на основании отдельных фактов из отдельных областей. Истина – конкретна.
Видимо универсальных кривых нет... И это – не плохо. В каждой области – свое… Надо быть адекватной ей.
5. Мы говорим об экономике в целом, о макро-экономике. Для экономики, как подсистеме социума, в конечном итоге важно гармоничное распределение доходов. В таком случае соответствующие кривые – это главные кривые экономики. И хорошо, что именно в макро-экономике такие кривые оказались «золотыми» по своим уравнениям.
Возникли и вопросы к авторам (которые, увы, задать было некуда). В «благополучной Европе» установившееся среднее отношение доходов по 10% самых богатых и бедных составляет ~1:7. Это гораздо выше «гармоничной кривой» в форме окружности, для которой такое отношение будет на уровне 1:44… (!?)
По состоянию же нынешнего анализа захотелось проверить многие выкладки авторов из МИФИ и заполнить пробелы.
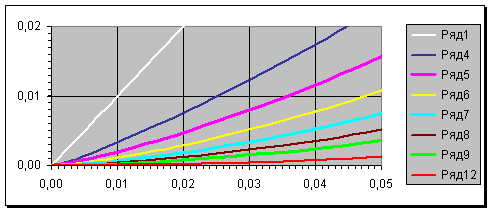
На нижнем рисунке представлены линии функции плотности вероятности «базового распределения МИФИ» без пропусков параметра «а», прежде всего 1,2 1,7. Просмотрите сами переходные процессы. Обратите внимание на линии «а=1,9» и «а=2,0».

На следующем большом рисунке представлена «диаграмма Лоренца» с линиями МИФИ без пропусков параметра «а» в районе «Золотых линий». Маленький рисунок графически демонстрирует ту ситуацию, что все «суммовые линии» МИФИ в начале координат имеют угол «0 » и на противоположном конце – «90 »…
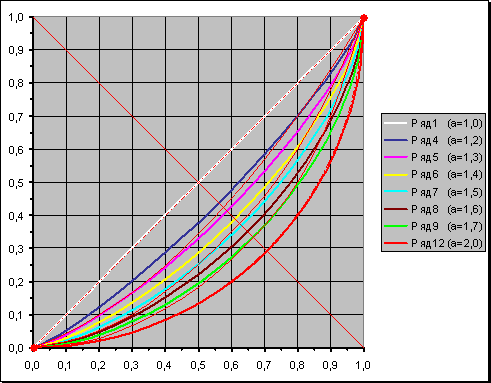
На нижнем рисунке совмещены «Золотые линии». Видно, что «А1» проходит вокруг базовой симметричной линии «а 1,25», «А2» — около линии «а 1,45», «А3» — около линии «а 1,65». Как раз, заполняя пространство, пропущенное в МИФИ, как просто переходное. Но вот именно здесь и образуется нечто важное…
Следующий
рисунок иллюстрирует ответ на вопрос, который повел далеко и ответил на один из
2-х главных вопросов этого пути. Сотрудники МИФИ, продвигаясь в своих
выкладках, привели, как промежуточную, формулу x(g). Не менее
интересно было увидеть обратную функцию: 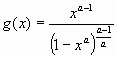 .
Здесь «х» — координата в «диаграмме Лоренца», а «g» — величина ресурса.
.
Здесь «х» — координата в «диаграмме Лоренца», а «g» — величина ресурса.
Итак, на нижнем рисунке представлены линии g(x) для ряда параметров «а».
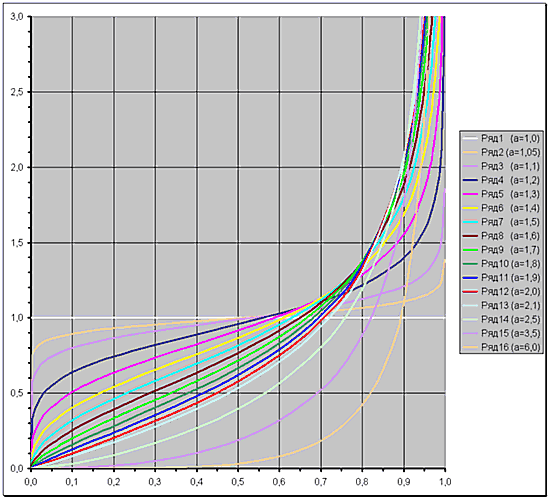
Не сразу эта красота посмотрелась по-другому. Восприятие должно было «насытиться» видами разных функций распределения, чтобы сформулировать здесь то, что стояло за красотой этой группы линий. Их соответствие линиям функций распределения увиделось четко после оглядки из следующих тем, когда приходилось бродить по множеству вопросов сразу…
Поверните верхний рисунок, чтобы поменялись местами оси координат, то есть посмотрите на эти функции, как на обратные. Вот они на нижнем рисунке.
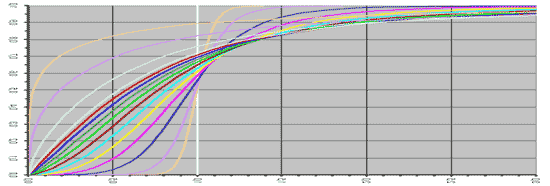
Увиденное привело к необходимости определиться с «функцией распределения»… Функцией распределения вероятностей (или кратко функцией распределения) называют функцию F(x), определяющую вероятность того, что случайная величина «x» примет значение, меньшее х0. Вероятность того, что непрерывная случайная величина «x» примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b. Потому функцию распределения называют также интегральной функцией.
Вернемся к нашим графикам. Вспомним смыслы диаграммы «шага_1». В координатной плоскости представления распределений «в суммовых относительных величинах» ось абсцисс была названа для случая распределения зарплаты – «количество зарплат по порядку от меньших нарастающим итогом, в %». Для распределения любого вообще ресурса данную ось можно было бы назвать так: «суммарное относительное (в %) количество единиц получения ресурса нарастающим итогом от меньшей величины ресурса». И в этой формулировке уже можно почувствовать «вероятностное» содержание этой оси. Ведь речь идет именно о накопительной сумме частот выпадения ресурса… А исходные суммируемые значения – есть статистический ряд…
Сделаем тогда 3-ю формулировку: «нарастающая сумма количеств событий, упорядоченных по количеству выпавшего ресурса». А «функция распределения» в некотором процессе и формируется значениями частот (вероятности) выпадения величин ресурса в сумме до данного, начиная с меньшего значения ресурса! А это значит, что наш график линий «В» и есть график функции распределения в обратных осях! В них оси абсцисс и ординат меняются, но это один и тот же график. И два системных подхода иллюстрации распределений, два способа представления статистических результатов, две системы координат линий выборок – это на самом деле взаимосвязанные выражения.
Итак, существующий набор описания статистических распределений содержит сейчас 2 исходных представления:
1.
функция распределения вероятностей f(r) (см.![]() 2)
2)
2. функция плотности вероятностей p(r) = df/dr.
Очевидно, для полноты представления необходимо ввести 3-ю составляющую – S(f) = z(f)df,
где r=z(f). Ее можно назвать функцией суммовых соотношений распределения или функцией накопительных частот (функцией накопительных вероятностей).
Правда, эта функция не всегда будет иметь простое алгебраическое выражение. Интеграл от функции, обратной функции распределения, будет сложным чаще всего. Поэтому всегда будет полезнее непосредственно видеть график накопительных вероятностей.
Посмотрим
цепочку действий при переходе от графика «суммовых относительных вероятностей»![]() 3
к графику плотности вероятности. Исходные условия суммовые относительные
координаты, то есть в диапазоне 0-100%.
3
к графику плотности вероятности. Исходные условия суммовые относительные
координаты, то есть в диапазоне 0-100%.
1. Дифференцирование функции S(f) (или построение по тангенсам касательных)
2. Получение обратной функции f(r) – функции распределения.
3. Дифференцированиеdf/dr
Всю цепочку действий можно назвать: «2 дифференцирования с преобразованием промежуточной функции в обратную».
Обратную цепочку действий можно назвать: «2 интегрирования с преобразованием промежуточной функции в обратную». Приведем ее.
1. Интегрирование функции плотности и получение функции распределения f(r) = p(r)dr
2. Получение обратной функцииr=z(f)
3. Получение интегральной функции S(f) = z(f)df и приведение ее к относительной шкале по оси ординат.
Мы все помним, что геометрический смысл определенного интеграла – это площадь под кривой интегрируемой функции. Но есть некий еще смысл и у неопределенного интеграла. Если вдуматься и посмотреть, то его «действие» связано с преобразованием системы координат. Интегральная функция как раз и преобразует ось ординат исходной функции в суммовую накопительную (но еще не относительную, не на отрезке 100%). Важно помнить: относительность оси ординат не сохраняется при интегрировании или дифференцировании. То есть приводить к относительности, к распределению на едином целом участке необходимо каждый раз «вручную».
И еще один комментарий, связанный с осью абсцисс «g» в графиках МИФИ. Сотрудники МИФИ преобразованием общих выражений вышли, в том числе на то, что функция распределения ресурса, полученная дифференцированием функции накопительных частот (как мы это теперь называем), дает значение не неких «реальных» величин ресурса, а поделенных на среднее арифметическое всей выборки. Само по себе это интересно и может быть полезно. Но, если иметь в виду, что это просто множитель, то необходимо затвердить главное. Одна и та же функция накопительных вероятностей может быть результатом разных по диапазону (min-max) выборок, но характер этих выборок будет один и тот же. Характер как раз и виден в функции накопительных вероятностей. То есть мы можем пропорционально растягивать или сжимать график f(r) по оси величин ресурса, или, что то же самое, вводить масштаб на оси «r», сохраняя при этом «характер распределения».
Вообще, чтобы легко можно было сопоставлять природу разных распределений на графике, координатную ось, по которой откладываются величины ресурса, лучше делать в относительных единицах: в %% от самого «mini» до самого «max».
В исходном тексте «Смысл экономики» акцентировалось внимание на том, что не имеет значения сама по себе величина разности между самой большой и самой маленькой зарплатами; значение имеет характер распределения между ними.
Возвращаясь к абстрактной математике, необходимо помнить следующее, когда мы имеем какую-то реальную выборку и строим ее представление в 3-х функциях. В этих функциях мы теряем конкретные «реальные» величины, но получаем емкое представление характера всего распределения.
Давайте попробуем увидеть общую закономерность изменения между линиями в суммовых относительных координатах и линиями плотности вероятности. Нас будет интересовать, прежде всего, какие изменения в последних надо ожидать (в каком направлении) при появлении эксцентриситетов первых линий относительно симметричных линий (базовых линий МИФИ).
Эксцентриситета может быть два:
- Ниже на начальном участке и
выше на конечном,
- Выше на начальном участке и
ниже на конечном.
Посмотрим, например, 2-ой случай. (Будем помнить, что оси координат преобразуются (дифференцированием функций) и меняются местами.)
Итак, исходной базовой линией в суммарной относительной системе координат возьмем линию «распределения МИФИ» с а=2, являющуюся частью окружности. Ее функция плотности распределения имеет форму «горки», промежуточную между «колоколом» и «гиперболой»; то есть легко можно будет представить ее эволюцию. Ну и, во-вторых, она имеет равномерную кривизну, что удобно.
Представим любую линию, которая от начала координат проходит выше этой базовой линии, а потом, естественно, ниже. «Золотые линии» пройдут, например, наоборот. Посмотрим чисто математически.
1. При прохождении линии сверху её тангенсы касательных будут сначала больше, потом меньше аналогичных величин базовой линии (имея между собой точку пересечения). На втором участке также будет 2-ая точка пересечения линий тангенсов касательных. Итак, в начале дифференциальная экспериментальная линия пройдет выше.
2. Это значит, что, как обратная функция, она в начале пройдет правее и дважды пересечет дифференциальную базовую линию.
3. Если тангенс её касательной в начале будет больше, чем у базовой, то на функции плотности это и отразится в повышении этого участка. Вопрос: больше или меньше будет этот тангенс для того, чтобы 2 раза пересечь дифференциальную базовую линию, находясь внутри неё (справа)?
4. Вообще то, она может пересечь базовую линию дважды в обоих случаях. Но более естественно и вероятно это произойдет, если в начале её тангенс будет больше тангенса базовой линии.
5. То есть можно говорить только о более вероятном варианте, что, если линия суммовых относительных величин «выпучивается» в верхней части относительно базовой линии, то ее линия плотности вероятности около начала координат будет подниматься вверх (в сторону гиперболы).
Если проверить эти выводы чисто по смыслу изменения конкретных величин, то есть цепочки «суммовые относительные группы величин ресурса» – «вероятность» – «плотность вероятности», то здесь тоже нельзя будет прийти к однозначному результату. Потому что по одной величине вероятности (и её разнице) нельзя судить о плотности вероятности. Результатом же в этом рассуждении будет то, что во 2-ом случае (экспериментальная линия в начале сверху) вероятность для ресурса будет меньше. То есть функция распределения пройдет ниже. Но какой при этом будет её угол? Он может быть, как больше, так и меньше.
Это общие тенденции. Но как на самом деле? Где реально «встанут» линии при этих возможных тенденциях «движения»? Ведь влияния очень сложны …
Это мы увидим в 4.2 и 4.3.
4.1 (так как нам пригодится остановиться и вспомнить)
Ниже представлены рисунки из полной версии (желающие могут получить ее через asa@tlt.ru) текста «http://www.trinitas.ru/rus/doc/0232/009a/02320025.htm».
Они представлены для опыта преобразований и сопоставления с действиями на следующих рисунках. На нижнем рисунке:
слева вверху: результат дифференцирования аппроксимированных линий «А», то есть линии «В1», «В2» и «В3», линии величин зарплаты в зависимости от суммовых относительных групп получателей.
слева внизу: эти же линии, но приведенные к одному диапазону (0.45 10)Эф, по которой определялись пропорции численности «среднего класса»;
справа вверху: диаграмма, аналогичная левой, но построенная по значениям тангенсов касательных к линиям «А»;
справа внизу: та же диаграмма, приведенная в относительные координаты (по ординате).
Несколько комментариев из «Смысла экономики».
Для
определения среднего слоя нужны конкретные величины дохода. «Граничные условия»
были приняты в долях от «эффективного эквивалента», скажем так «социального
воспроизводства» — Эф. Мы знаем, что при других «граничных условиях»
характер суммовых линий «А» останется тот же![]() 4.
Но вот количественные результаты доли «среднего слоя» в обществе связаны с
принятыми значениями минимальной и максимальной зарплаты.
4.
Но вот количественные результаты доли «среднего слоя» в обществе связаны с
принятыми значениями минимальной и максимальной зарплаты.
Теперь перейдем к рисункам текущего анализа. В начале одна ремарка.
Функции распределения достигают значения «1» в бесконечности. В практических задачах распределения ресурсов это неприемлемо. В этих задачах значения конечны. Пытаясь применить для их иллюстрации те или иные стандартные распределения, необходимо в суммарной вероятности дойти до «1» на определенном значении. Это можно сделать по-разному и вывести определенные корректирующие зависимости. Но здесь достаточно ограничиться величиной на графике абстрактного (формульного) распределения, при которой, например, pi=99% или pi=95%.
Итак, на нижнем рисунке:
слева вверху: уменьшенная предыдущая диаграмма линий распределения МИФИ в суммовых относительных координатах;
слева внизу: уменьшенная предыдущая диаграмма реальных значений величин из верхней диаграммы (дифференцированием), которая как x=f(y) является функцией распределения;
справа вверху: диаграмма, аналогичная левой-нижней, но построенная по значениям тангенсов касательных к линиям правой диаграммы;
справа внизу: та же диаграмма, приведенная в относительные координаты (по ординате).
Интересно сопоставить правую верхнюю и левую нижнюю диаграммы. Интересна также наглядность относительных координат из сопоставления двух правых диаграмм.

4.2 (так как нам придется еще немного поговорить на общие темы)
Потому что «напрашивается» пройтись от известных стандартных распределений к представлениям их в «суммовых относительных величинах». Давайте теперь в дополнение к табличным данным «шага_3» посмотрим и их функции распределения.
Распределение Гаусса:
функция распределения определена только как канонический ее интеграл.
Вот
один из вариантов: 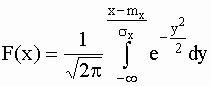
Распределение
Вейбулла: функция
распределения ![]()
Распределение
Парето:
интегрированием плотности (см. таблицу в п.2) получим функцию распределения: ![]() .
.
Конечно, интересно получить для этих распределений формулы функций «накопительный вероятностей» и посмотреть их графический вид. Для этого, напомним, необходимо взять интеграл от функции, обратной функции распределения.
Распределение Гаусса пропустим... Для распределения Вейбулла получаем:
 ,
где z – функция распределения F(x).
,
где z – функция распределения F(x).
Трудно не ошибиться при взятии такого интеграла. Хотя и было бы интересно посмотреть на координатной плоскости «суммовых относительных величин» как сойдутся в углы (0, 0) и (100%, 100%) линии, построенные по полученным «интегральным зависимостям», и какова при этом будет форма у этих «стандартных распределений»…
Попробуем
с распределением Парето. Здесь проще; вот результат интегрирования функции,
обратной функции распределения: ![]() .
.
В
частном случае при m=1 и n=0 получаем: ![]() .
.
На нижней диаграмме сплошными цветными (кроме красных) линиями представлены результаты вычислений по верхней формуле (z=0 1) с приведением их к относительной шкале. Надо сказать, что реальные линии, посчитанные по этой формуле, находятся в отрицательной области. При значениях а<1 расчетные линии проходят в положительной ординате, имея тот же характер и скачком обрываясь в «0» при z=1.
Для сравнения красной линией нанесены «Золотые линии».
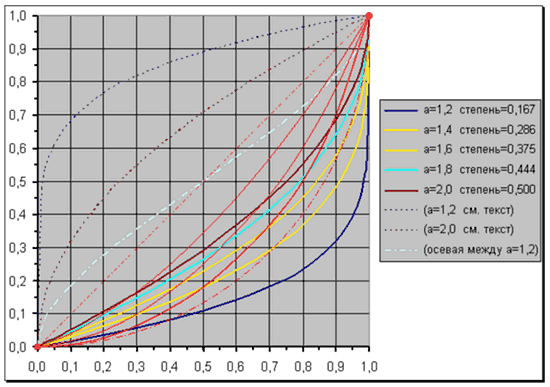
Для
сравнения на эту графическую плоскость нанесены пунктиром аналогично
построенные линии от формулы ![]() ,
то есть по «чистой степени»: для 2-х значений «а» и осевая (или средняя) между
линиями с а=1,2.
,
то есть по «чистой степени»: для 2-х значений «а» и осевая (или средняя) между
линиями с а=1,2.
Какие следуют выводы?
Во-первых, все распределения Парето на суммовых относительных диаграммах имеют верхнюю выпуклость (эксцентриситет), что правильно говорит о быстром нарастании владения ресурсом по мере приближения к наиболее владеющим.
Во-вторых, для данного распределения подтвердилось, что прохождение линий ниже базовых в начале на суммовых относительных диаграммах приводит к подъему вверх линий в начале функций плотности вероятности (гипербола Парето).
Во-третьих, наблюдение за характером этих линий утверждает в правильности аппроксимации «Золотых кривых» через параболу и показательную функцию, в правильности выделения параболического и показательного коридоров и, соответственно, в правильности выводов текста «Смысл экономики».
4.3 А теперь вернемся и пойдем дальше.
Пойдем теперь с другой стороны. От «Золотых кривых» — к функциям плотности распределения в соответствии с порядком действий, описанном до (4.1). Эта цепочка действий называлась, как помним, «2 дифференцирования с преобразованием промежуточной функции в обратную». После первых 2-х действий мы получаем функцию распределения f(r).
На нижнем рисунке представлены сплошными линиями кривые функций распределения В1, В2 и В3, приведенные к относительной шкале. Сравните их с линиями на левом нижнем рисунке в начале (4.1).
Пунктиром повторно приведены линии функции распределения МИФИ, на этот раз приведенные к относительной шкале при максимальном значении вероятности в 99%.

Второе дифференцирование «золотых кривых» дает следующие формулы:
![]()
![]()
![]()
Эти графики плотности вероятности распределений, представленных «золотыми кривыми» в интегрально-относительных координатах, приведены на нижнем рисунке. Здесь же повторены 3 линии из распределения МИФИ.
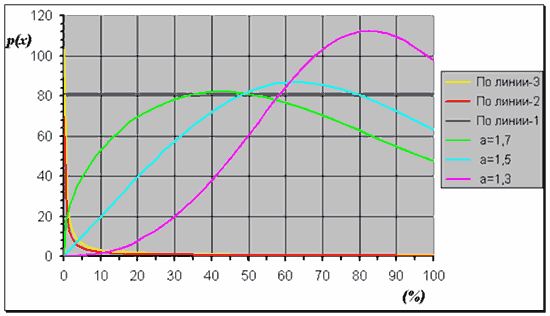
Ну что ж, экстремальный (в сторону Парето) характер плотности для линий «2» и «3», с одной стороны, ожидался. Правда, учитывая «переходность» «А2», предполагалось, что она будет не так близка к «А3», тем более снизу. С другой стороны, как предполагалось из общего рассмотрения взаимного влияния изменений в 2-х формах представления, эти линии должны были сдвинутся по отношению стандартных линий МИФИ в сторону гауссовых. Ну что ж, как есть. Опять же, если нет ошибок в расчетах и сделаны правильные выводы…
Но вот интересен константный характер линии плотности вероятности у главной линии «А1». Эта линия – самая средняя между «гиперболой Парето» и «колоколом Гаусса», средняя между 2-мя крайностями. О «средней линии», о смысле «нормально-краевых распределений» мы как раз будем говорить во 2-ой части. А здесь еще вот, что интересно. Константный характер, то есть равновероятный. Равновероятная линия – то есть равновозможная. Интересная игра слов: равновозможное распределение – это распределение равных возможностей. Равных возможностей – то есть не единообразных, уравнительных, но разно-образных для разных личностей, позволяющих реализоваться личностному разнообразию, но без удушающей дифференциации по возможностям.
Да, это гипотеза, что есть распределение ресурсов (доходов), наиболее адекватное разнообразию людей и возможности оптимальной творческой самореализации в процессе «социумного воспроизводства». Предполагаем, что такое распределение – квадратичное в суммовых относительных величинах. Социологическую проверку этой гипотезы можно воспринимать, как задачу.
Остается только найти, в каких стандартных распределениях может также встречаться такая линия плотности. Первое – это в бета-распределении (введенном Джини в 1911 г.). Функция его плотности выражается так:

Сама бета-функция иногда так выражается через гамма-функцию (см.ниже):
![]()
Вид прямой линии «y=1» будет при a=1 и b=1. Ее можно увидеть точечной линией на нижнем рисунке.
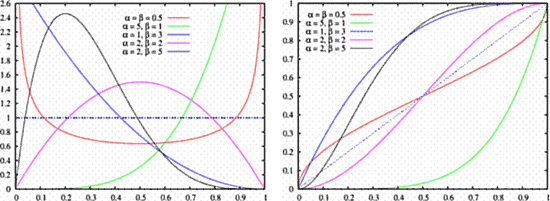
И линию плотности, близкую к прямой линии, можно увидеть в гамма-распределении (введенном Везерберн в 1946 г.). Функция его плотности выражается так:
![]() ,
где
,
где 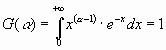 с тем, чтобы
с тем, чтобы ![]()
Вид, близкий прямой линии, будет в диапазоне параметров =1 1,5 и <0,1
Опять же гамма-распределение при разных своих параметрах имеет линии плотности, аналогичные по виду распределению МИФИ и распределению Вейбулла.
В заключение – 2 комментария по общим вопросам.
По поводу коэффициента Джини. Подобно «диаграмме Лоренца» для меня, упоминание коэффициента Джини в каких-то последующе попавшихся текстах было, как «старая новость»; из постановки фраз понималось так, что он работает просто с площадью под кривой. Разумеется, не преминулось его посчитать. Для 2-ой (средней) кривой «А» он ~0,65 (для y=0,01x2 ~0,[6]). Для 3-ей (нижней) — ~0,55. Окружность проходит еще ниже (на ~0,43=2-0.5). Гармоничные распределения, в частности доходов, как мне представляется, проходят между 1-ой и 2-ой кривыми; там так называемый коэффициент Джини больше 0,65 (до ~0,8). «Гармоничными» по к.Джини считаются кривые, у которых он равен ~0,62 (то есть Золотой Пропорции); а значит соответствующие кривые проходят между 2-ой и 3-ей Золотыми А-линиями. Здесь явное расхождение во мнениях. Мне представляется, что подход заочных оппонентов слишком прост и механистичен…
Площади не отражают (плохо отражают) характер (качество) распределений (к-нт Джини — тривиален, его суть – это формальная математика без привязки к конкретной действительности; он идет просто от «физического смысла» и отношений кривых на графиках). Распределения выражаются рядами, последовательностями и, соответственно, формулами кривых.
Коэффициент Джини не реагирует на форму кривой, не замечает под одинаковой площадью разный характер линий, а последнее в суммовых относительных координатах, как Вы убедились, главное. Он – это некий «валовый» грубый инструмент, которому не подвластны тонкие движения, изменения. А в социальных объектах всё тонко, все находится в движении, изменения которого должны улавливаться.
И еще по одному поводу. Гауссова кривая плотности показывает распределение (статистику) более-менее пологого и симметричного колокола вокруг средней величины. В интегрально-относительной системе координат можно сказать, что линии тоже проявляют статистику вокруг среднего значения. Но сама парадигма среднего значения в ней не интересна, не полна для конкретного управления. Сравним, например, 2 образа линий, несущих один смысл в 2-х системах представления. В интегрально-относительной системе прямая y=x это одинаковая у всех зарплата, то есть абсолютная уравниловка. В системе плотности вероятности это будет вертикальный отрезок посередине. Абсцисса, разделяющая «колокол» на равные площади, соответствует одинаковым количествам значений исследуемого параметра слева и справа (одинаковой вероятности), и ордината этой точки — это соответствующее значение параметра. А на интегрально-относительном графике эта абсцисса «одинаковых количеств значений» равна всегда 50%, она тоже дает некоторую ординату для разных кривых. Например, такая ордината для «кривой уравниловки» равна 50%, для «кривой А1» равна 35%, для кривой А2 — 25%, для кривой А3 — 18%, для «окружности» — 13%... Но, конечно, смысла «равновероятности» эти ординаты здесь не несут; это значение среднего по выборке.
Вообще, в этом поиске пересекаются, «микшируются» смыслы «статистической обработки результатов измерения» и «анализ явлений через распределение его ресурсов». На одном инструментальном поле у них разные цели: одна ищет правильное значение в разбросе результатов, а другому интересно само распределение, закономерности и последствия…
(Продолжение следует)
·
![]() 1) Эти файлы я могу выслать
желающим; но некоторые объекты формул в них выводятся не правильно.
1) Эти файлы я могу выслать
желающим; но некоторые объекты формул в них выводятся не правильно.
·
![]() 2) r - измеряемая
величина (величина ресурса). Вообще, функция распределения обозначается по
разному: F(x), Ф(x), f(x). Здесь остановились на варианте с маленькой буквы,
потому что эта функция сама находится в важном подынтегральном выражении, как
обратная функция (см. дальше).
2) r - измеряемая
величина (величина ресурса). Вообще, функция распределения обозначается по
разному: F(x), Ф(x), f(x). Здесь остановились на варианте с маленькой буквы,
потому что эта функция сама находится в важном подынтегральном выражении, как
обратная функция (см. дальше).
·
![]() 3) Можно также назвать «
интегрально-относительный график распределения ресурса» или
«интегрально-относительный спектр ресурса».
3) Можно также назвать «
интегрально-относительный график распределения ресурса» или
«интегрально-относительный спектр ресурса».
·
![]() 4) Например, у прямой с любым «k»
суммарное нарастание площади происходит по функции y=x2.То
есть угол наклона прямой «величины зарплаты», а значит и соотношение min и max
зарплаты не имеет значения для характера «суммовых распределений». Вид ее
кривой останется неизменным.
4) Например, у прямой с любым «k»
суммарное нарастание площади происходит по функции y=x2.То
есть угол наклона прямой «величины зарплаты», а значит и соотношение min и max
зарплаты не имеет значения для характера «суммовых распределений». Вид ее
кривой останется неизменным.
Сергей
А. Алферов, Несколько шагов в интересную сторону… (часть 1) // «Академия
Тринитаризма», М., Эл № 77-6567, публ.13926, 23.10.2006