Моделирование маятника Милковича в Живой Физике

Бакунин В.В.

1. Описание подготовки эксперимента.

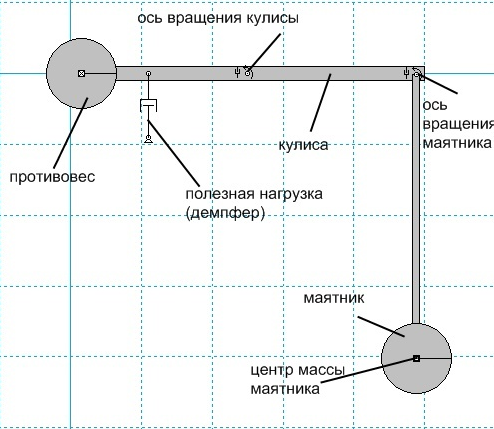
Маятник Милковича представляет из себя в статическом положении уравновешенный рычаг (кулису), один конец которого нагружен грузом или растянутой (сжатой) пружиной, или тем и другим вместе, а другой конец – свободно весящим маятником (рис.1). При раскачивании маятника на его ось действует знакопеременная периодическая сила, что вызывает качание кулисы. При создании на кулисе полезной нагрузки в виде насоса, молота (и др.), или непосредственно на оси кулисы, т.е. знакопеременной полезной нагрузки, происходит снятие мощности.

Рисунок 1. Маятник Милковича

Целью эксперимента было получение графиков полезной (выходной) мощности и затраченной (входной) мощности как функций от времени, определение мгновенной (за временной шаг измерения) работы входа и выхода, их разности, определение работы выходной и входной нагрузки за период маятника, а также предварительный анализ распределения выходной и входной работы во времени.

Поскольку автор проводил в своё время натурный эксперимент, то за параметры модели были взяты параметры, приближенные к натурному опыту: кулиса длиной 0,5 м, массой 0,2 кг (дерево), маятник 1,2 кг, штанга маятника 0,02 кг(специально занижена с целью сосредоточения центра масс маятника в его грузе), длина маятника от оси вращения до центра массы 40 см противовес 1,22 кг. Центр массы противовеса и оси маятника на одинаковом расстоянии относительно оси вращения кулисы.

Стабильная работа маятника Милковича возможна, если подкачка маятника внешней силой синхронизирована с собственной частотой колебания маятника (явление резонанса), а величина нагрузки (демпфирование) достаточная, чтобы маятник не пошёл в разнос, а совершал автоколебания. Чтобы избежать высчитывания собственной частоты колебаний маятника или получения её экспериментальным путём было принято простое решение – задать подкачивающую силу пропорционально скорости центра массы маятника:

                                                                                 (1),

где – начальная небольшая сила, обеспечивающая страгивание маятника,

– проекция скорости центра масс маятника на ось действия подкачивающей силы,

К – масштабный коэффициент.

В ЖФ это было реализовано созданием горизонтальной силы, приложенной к центру масс маятника, в свойствах горизонтальной проекции которой введено следующее выражение:

                          (1а),

- скорость центра масс маятника .

Это выражение позволяет, во-первых, задать направление силы, совпадающее с направлением скорости движения, во вторых, менять максимальное значение силы до нулевого (практически) в зависимости от изменения скорости, тем самым обеспечивая синхронное подкачивание. Масштабный коэффициент был получен экспериментально в соответствии с подбором коэффициента демпфирования полезной нагрузки таким образом, чтобы маятник совершал колебания на угол порядка 45 градусов.

              Оси вращения маятника и кулисы были организованы в виде выбора такого инструмента в Живой Физике (ЖФ) как демпфер вращения с целью учёта трения на осях через возможность задания сопротивления в виде коэффициента демпфирования в инструменте демпфер вращения.

Поскольку выходная мощность – это сумма мощностей, снимаемых с полезной нагрузки (демпфера) и мощностей, идущих на преодоление трения в осях маятника и кулисы, то было принято решение не распыляться, а предположить, что вся снимаемая мощность сосредоточена в полезной нагрузке (демпфере), которая включает в себя мощности трения осей. Для этого коэффициенты демпфирования демпферов вращения осей заданы 0. Коэффициент демпфирования на демпфере был подобран экспериментально и равен 50 исходя из условия приблизительной одинаковости угла качания кулисы относительно горизонтальной оси.

В пункте меню ЖФ было выбрано измеритель угла для кулисы и маятника, измеритель мощности для демпфера. Дополнительно в измеритель мощности для демпфера была введена формула для подсчёта мгновенной мощности подкачивающей силы как произведение мгновенной силы на мгновенную скорость:

                                                      (2).

В ЖФ эта формула реализована аналогично формуле для демпфера:

constraintforce(18).x * constraint[18].dv.x (2а),

где constraintforce(18).x – проекция силы подкачки (1а) на ось X,

constraint[18].dv.x – скорость этой силы на ось X.

Так как в свойствах силы подкачки [18]была поставлена галочка «Поворачивать с телом», то проекция на ось X – это и есть полная сила и скорость. Поэтому их произведение даёт мгновенную мощность подкачки.

Также был создан дополнительный измеритель для определения мгновенных работ на подкачке и демпфере, а также их разности. Мгновенная работа определяется произведением мгновенной мощности на шаг эксперимента по времени (0.025 с):

                                               (3).

В ЖФ это реализовано так:

Output[19].y1*0.025

Output[19].y2*0.025                                                     (3а),

где Output[19].y1 – значение измерителя [19] по оси y1 (мгновенная мощность на демпфере),

Output[19].y2 – значение измерителя [19] по оси y2 (мгновенная мощность на подкачке).

Разность работ:

(4).

 

2. Эксперимент.

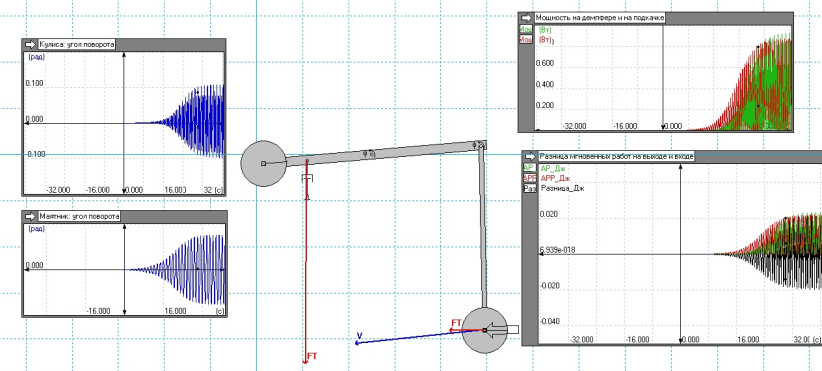
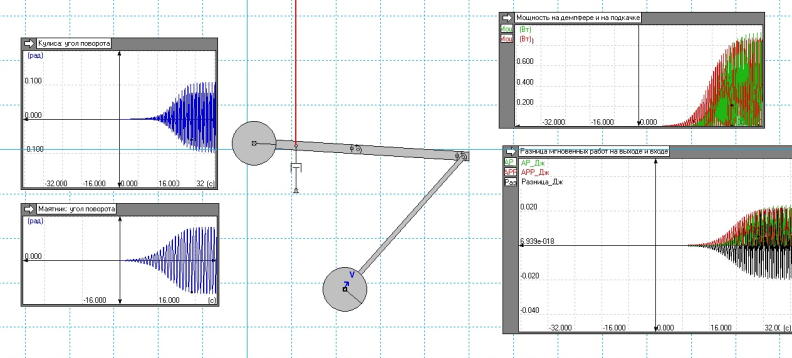
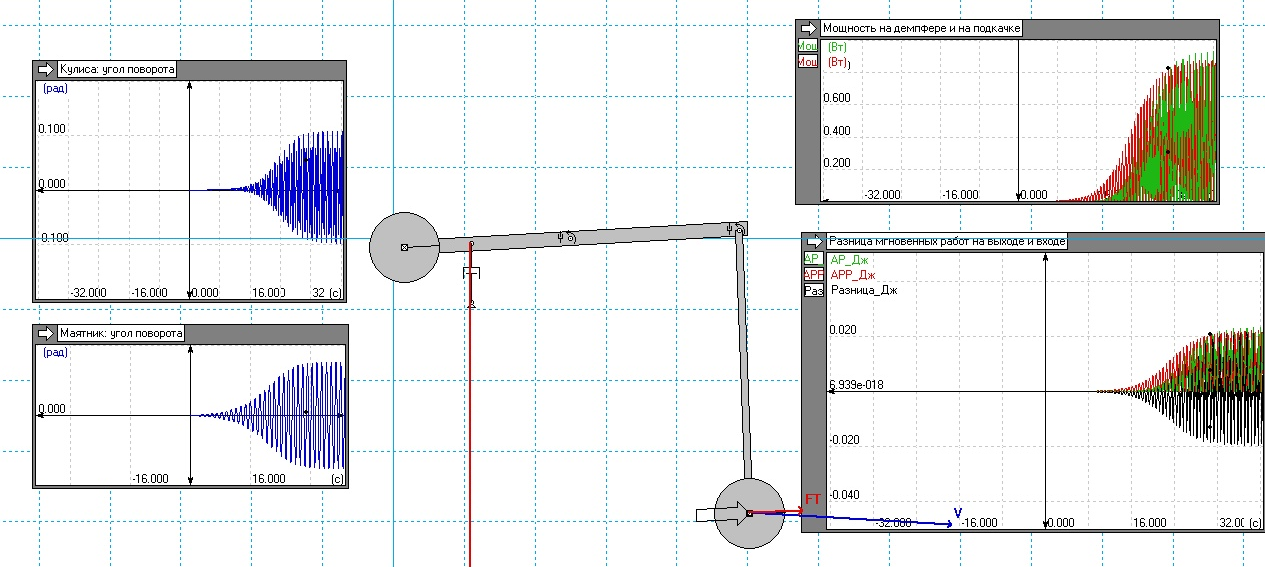
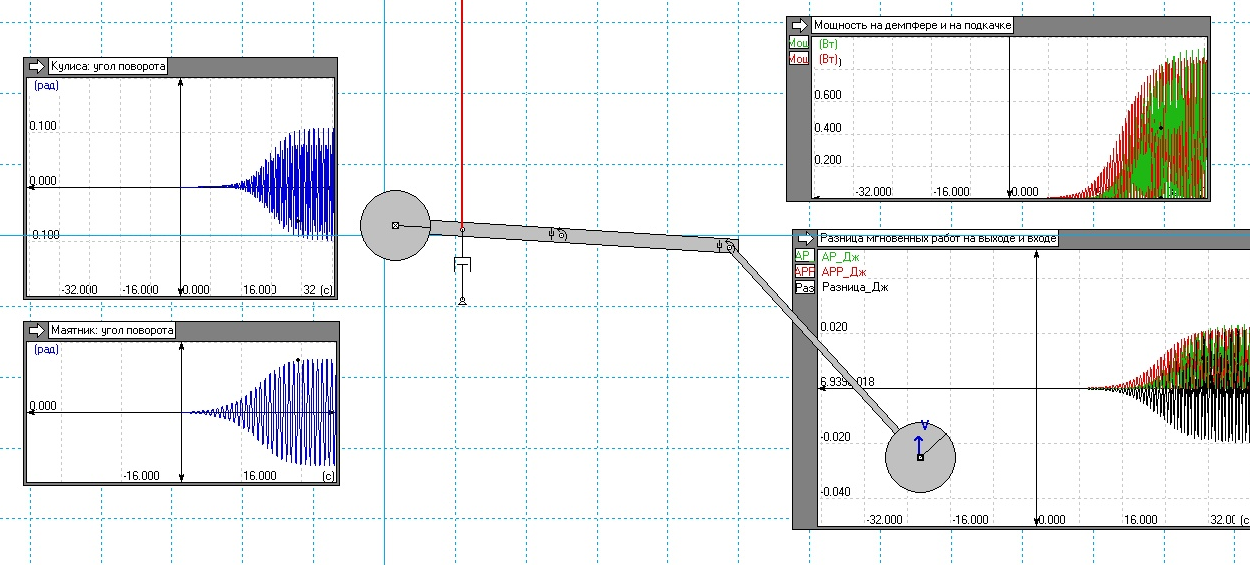
После запуска эксперимента постепенно увеличивающаяся сила подкачки раскачивает маятник и доводит угол его раскачки до максимально возможного для данных параметров механизма. Основные критические положения маятника за один период представлены на рис. 2.

Рис. 2 Кинематика движения маятника за период

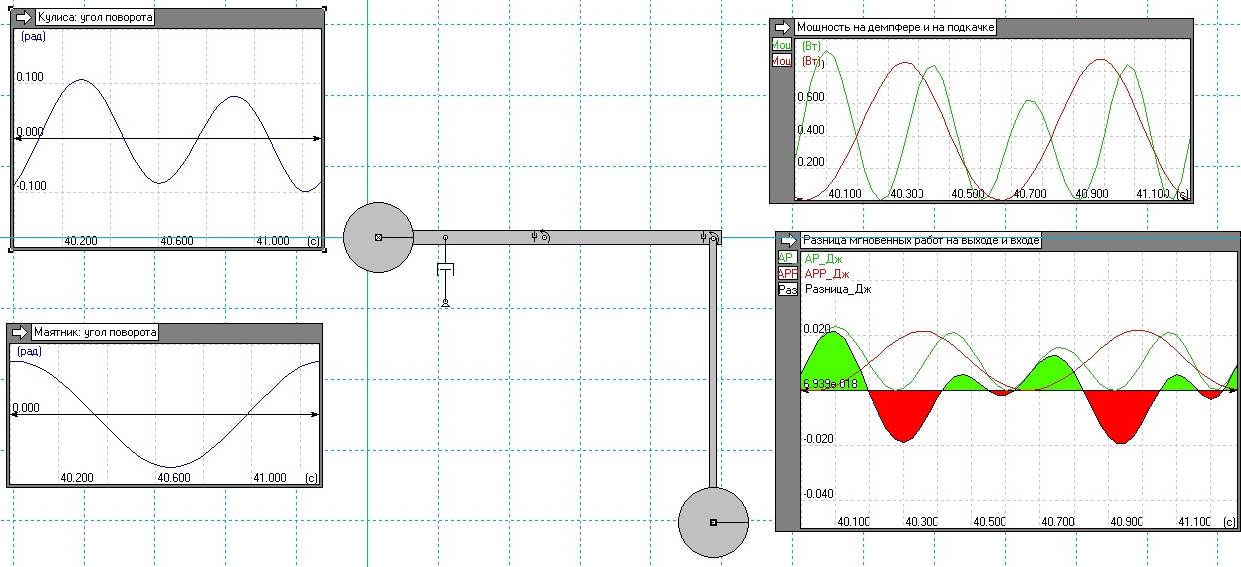
              После выхода маятника на стабильный режим работы эксперимент был остановлен. Для более тщательного изучения мощностей масштаб вывода графиков был увеличен за счёт выбора временного интервала – за период качания маятника 1,28 с (от 40 до 41,28), рисунок 3. Зелёным представлен график выходной мощности устройства (демпфера), а красным – входной мощности (подкачки).

              Чтобы убедиться – есть ли какой-либо выигрыш в работе на выходе устройства достаточно проинтегрировать разность работ входа и выхода за период подкачки, т.е. по большому счёту сравнить суммы зелёных и красных площадей за период работы маятника (рис.3). Визуально всё чико в чику, выигрыша нет.

Непосредственной функции интегрирования (суммирования) в ЖФ я не нашёл, поэтому перенёс результаты эксперимента в таблицу 1, а затем базу данных эксперимента в Маткад, где благополучно проинтегрировал.

Рис. 3 Разница мгновенных работ на демпфере (выходе - зелёным) и на подкачке (входе – красным)

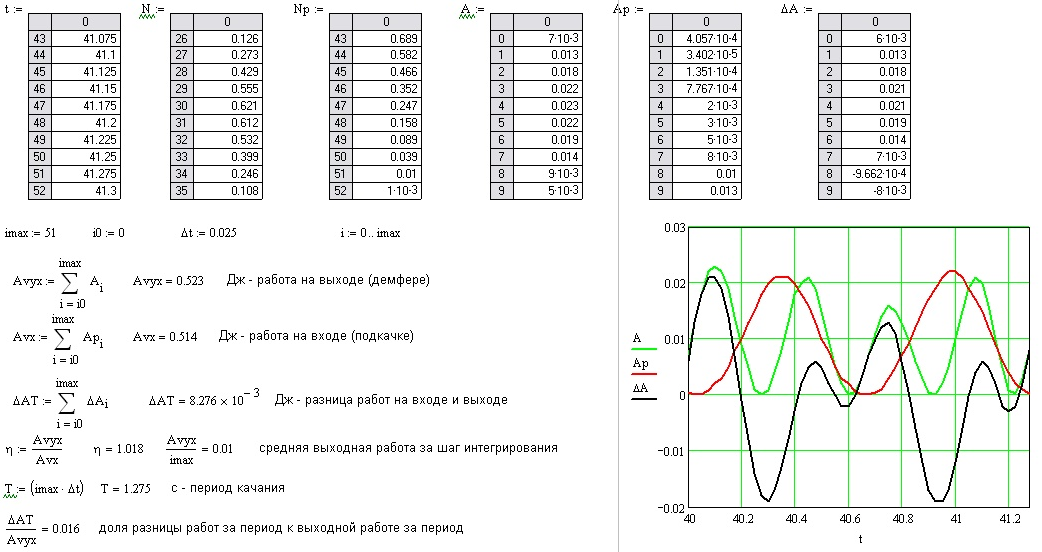
              Результаты интегрирования представлены на рисунке 4.

Рис. 4 Результаты интегрирования

Как видим, разница «выигрыша» и «проигрыша» составляет 0, 008 Дж, что меньше чем средняя работа за шаг интегрирования (0,010 Дж). Это говорит о том, что разница на уровне ошибки интегрирования и реального выигрыша нет.

3. Выводы

 

1) Параметры механизма маятника были выбраны во многом случайным образом, только лишь с целью его стабильной работы (автоколебания). По этим выбранным параметрам при моделировании в ЖФ выигрыша в выходной работе по отношению ко входной за период работы маятника нет.

2) Казалось бы, тему можно закрыть, но одно наблюдение заставляет задуматься о природе таких колебаний, когда входной импульс передаётся не мгновенно, а за достаточно ощутимый по отношению к единице жизни маятника (периоду его колебания) период времени. Это смещение «выигрышей» (зелёное на рис. 3) и «проигрышей» (красное). Скорее сего это связано с моментом инерции элементов механизма (кулисы, груза и т.д). Это наблюдение наталкивает на мысль, что маятник Милковича более открытая система, чем простой удлинённый рычаг, в котором импульс передаётся почти мгновенно. Ведь пока длится период «выигрыша» с параметрами окружающей среды могут происходить изменения, приводящие к изменению поведения маятника. Или эти изменения могут быть вызваны искусственно.

3) Следует глубже исследовать работу механизма на предмет дисперсионного анализа его параметров, т.е. провести планирование эксперимента, что в ЖФ сделать гораздо быстрее, чем в натуре.

4) Полезная нагрузка в виде демпфера может быть не «пассивной», а «активной», т.е. иметь закон изменения, например, коэффициента демпфирования созвучным (синхронным) с колебанием кулисы.

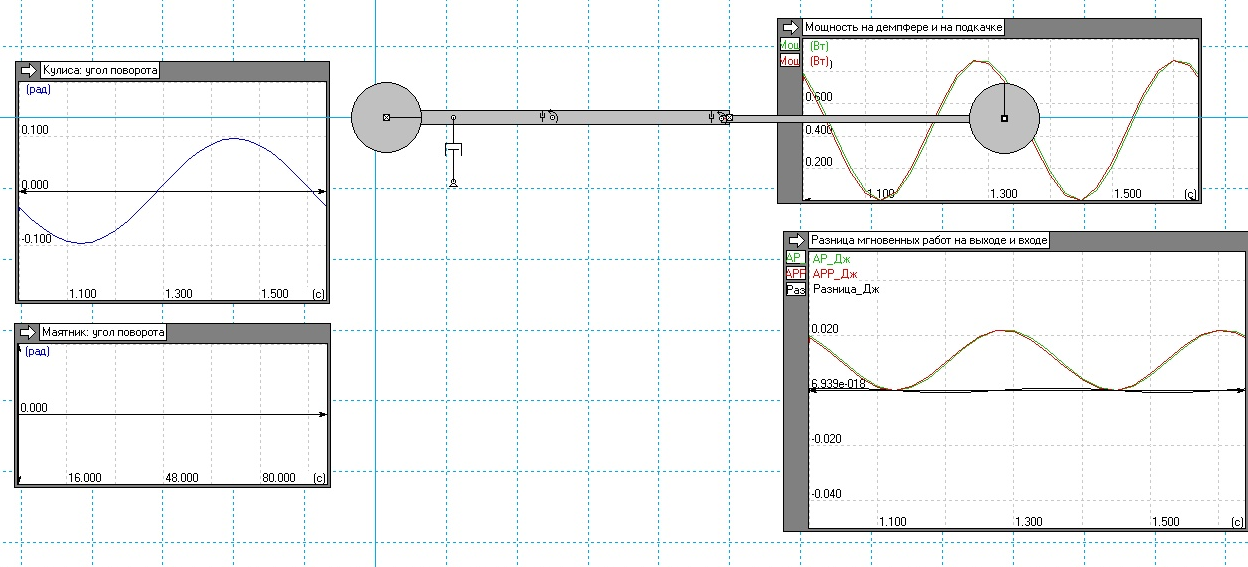
5) Возникло некоторое определение маятника Милковича – это «надломленный» простой рычаг, которым Архимед готов был перевернуть мир. Действительно, если провести обратную операцию – повернуть маятник до уровня кулисы, закрепить его, убрать массы противовеса и маятника (уравновесить), задать нужную знакопеременную нагрузку – мы получим простой рычаг с теми же выходными параметрами, но на котором импульс передаётся мгновенно. (рис. 5). Только маятник Милковича несколько более компактен.

 

 

Рис.5 Простой рычаг с теми же выходными параметрами, что и маятник Милковича

 

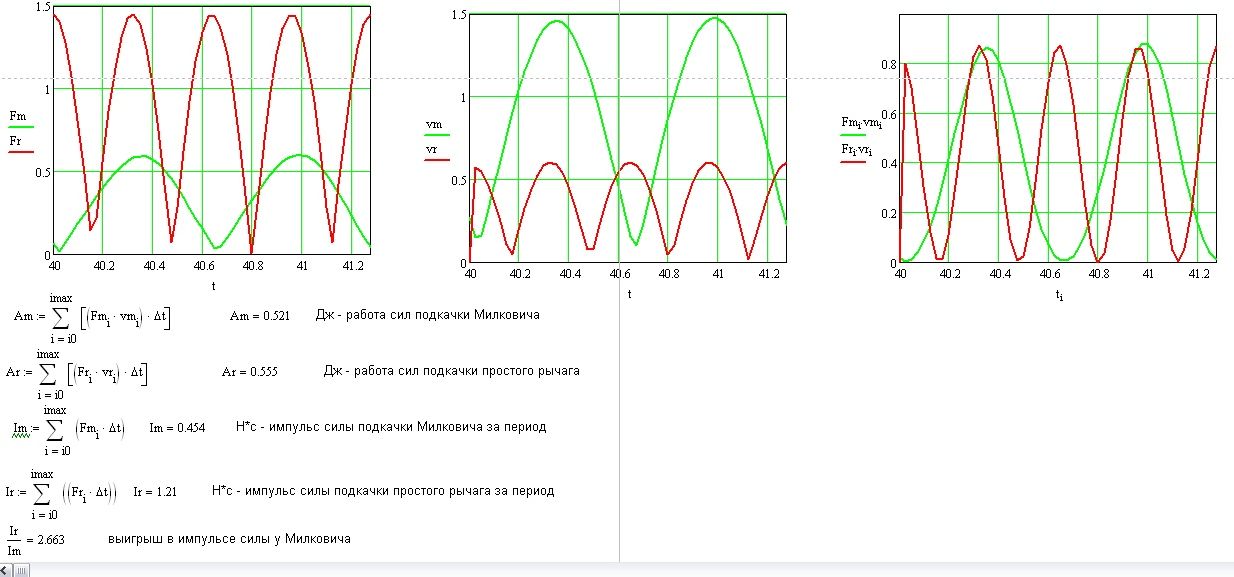
Рассмотрев за одно и тоже время (период работы маятника Милковича) подкачивающую силу как для маятника Милковича, так и для простого рычага (рис.6), видим, что работа за период одинакова (в пределах ошибки интегрирования), а вот у Милковича - почти в 2,7 раза меньше, чем у простого рычага. Вообще импульс силы в любом преобразователе (например, рычаг в механике твёрдого тела, гидродомкрат в гидравлике, тепловой насос в теплотехнике, электротрансформатор в электротехнике) разный на «плечах» преобразователя.

Рис.6 Выигрыш в импульсе силы у маятника Милковича. Зелёным – подкачка у маятника Милковича, красным – у простого рычага. F – силы, v – скорости, F*v – мощности.

 

Таблица 1. Результаты эксперимента за период работы маятника Милковича