ПРИЛОЖЕНИЕ 1а
Р. Фейнман
Об импульсе независимых электрического и магнитного полей
Из учебного пособия для студентов
ВУЗов. Р. Фейнман, Р. Лейтон, М. Сэндс.
Фейнмановские лекции по физике. Т 6.
Электродинамика,
Изд. "МИР", М., 1977.
ПОСТАНОВКА ВОПРОСА (стр. 59 - 61)
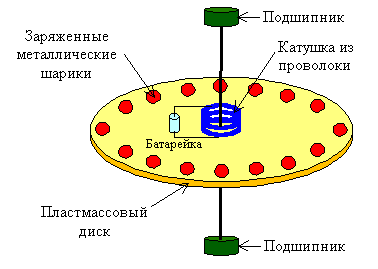
Представим, что мы конструируем прибор (см. рисунок), в котором имеется тонкий круглый пластмассовый диск, укреплённый концентрически на оси с хорошими подшипниками, так что он совершенно свободно вращается.

На диске имеется катушка из проволоки - короткий соленоид,
62
концентричный, по отношению к оси вращения. Через этот соленоид проходит постоянный ток I от маленькой батареи, также укреплённой на диске. Вблизи края диска по окружности на равном расстоянии размещены маленькие металлические шарики, изолированные друг от друга и от соленоида пластмассовым материалом диска. Каждый из этих проводящих шариков заряжен одноимённым зарядом Q. Вся картина стационарна, и диск неподвижен. Предположим, что случайно, а может и намеренно, ток в соленоиде прекратился, но, разумеется, без какого-либо вмешательства извне. Пока через соленоид шёл ток, более или менее параллельно оси диска проходил магнитный поток. После того как ток прервался, поток этот должен уменьшится до нуля. Поэтому должно возникать индуцированное электрическое поле, которое будет циркулировать по окружности с центром на оси диска. Заряженные шарики на периферии диска будут все испытывать действие электрического поля, касательного к внешней окружности диска. Эта электрическая сила направлена для всех зарядов одинаково и, следовательно, вызовет у диска вращающий момент. Из этих соображений можно ожидать, что, когда ток в соленоиде исчезнет, диск начнёт вращаться. Если нам известны момент инерции диска, ток в соленоиде и заряд шариков, то можно вычислить результирующую угловую скорость.
Но можно рассуждать и по другому. Используя закон сохранения момента количества движения, мы могли бы сказать, что момент диска со всеми его пристройками вначале равен нулю, поэтому момент всей системы должен оставаться нулевым. Никакого вращения при остановке тока быть не должно. Какое из доказательств правильно? Повернётся ли диск или нет. Мы предлагаем вам подумать над этим вопросом
.Хотелось бы предостеречь вас, что правильный ответ не зависит от всяких несущественных факторов, таких как несимметричное положение батареи, например. В самом деле, вы можете представить себе такой идеальный случай: соленоид сделан из сверхпроводящей проволоки, через которую проходит ток. После того как диск тщательно установлен неподвижным, температуру соленоида медленно начинают повышать. Когда температура проволоки достигнет переходного значения между сверхпроводимостью и нормальной проводимостью, ток в соленоиде обратится в нуль вследствие сопротивления проволоки. Поток, как и раньше, упадёт до нуля и вокруг оси
63
возникнет электрическое поле. Мы хотели бы также предостеречь вас, что решение не простое, но это и не обман. Когда вы разберётесь в этом, вы обнаружите важный закон электромагнетизма.
ОТВЕТ (с. 304)
Ответ на этот вопрос такой: если у Вас есть магнитное поле и какие-то заряды, то поле имеет и момент количества движения. Он возник ещё при создании самого поля. Когда же поле выключается, момент количества движения отдаётся обратно *). Так что диск …
начнёт крутиться **).*) Рассматриваемая задача при некоторых условиях, налагаемых на геометрические параметры системы, имеет точное аналитическое решение (см. "Часть II, Глава 1" и "Приложение 2"), согласно которому момент количества движения приобретаемый системой в результате действия электрического поля индукции на заряды ровно в два раза превышает момент количества движения независимых друг от друга электрического и магнитного полей системы (студенты третьего курса физических специальностей смогут без особых затруднений проверить это прямыми вычислениями). Таким образом предлагаемое Р. Фейнманом объяснение предсказанного им вращения диска не выдерживает критики. Соответствующее объяснение, полностью удовлетворяющее фундаментальным положениям классической электродинамики, дано на страницах этой книги.
**) Р. Фейнман не учёл приложенный к кольцу с током момент, так называемой, магнитодинамической силы , который в точности компенсирует моменты сил индукции, приложенные к периферийным зарядам. Таким образом, рассматриваемая система является замкнутой по моменту количества движения и посему не нуждается в привлечении гипотезы об импульсе стационарных полей. Диск будет стоять на месте.
64
Размещено на сайте 12.02.2016.
Статьи других авторов
На главную