Проблема скрытого импульса и ее решение или новые горизонты классической электродинамики

© Георгий Петрович Иванов

Написать автору: nara@tts.lt

• Анализ примеров приведенных в научной литературе.
• Вывод о существовании сил (моментов сил), не имеющих реакции противодействия со стороны вещественных и полевых элементов, входящих в систему.
• Вывод о фактической незамкнутости замкнутых по общепринятым критериям систем.
• Вывод о существовании новой формы материи, отличной от вещества и поля.

Объектом исследования настоящей работы является малоизвестная область на стыке классической электродинамики и механики, касающаяся не связанных с излучением электромагнитных волн явлений механического движения, имеющих место в замкнутых, по традиционным представлениям, системах, при наличии квазистационарно меняющихся независимых друг от друга электрического и магнитного полей (неволновых полей - nonradiating fields).

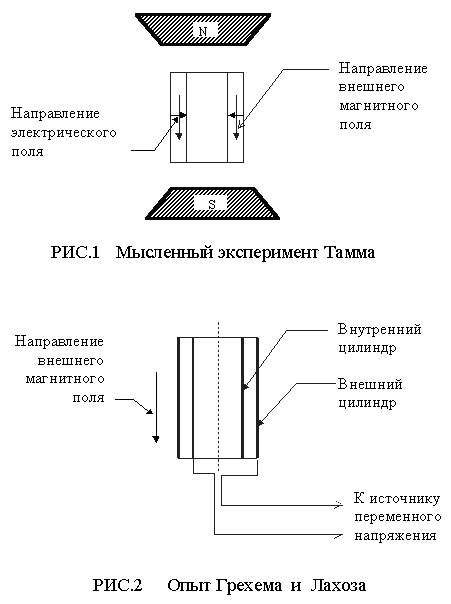
В “Основах теории электричества” И. Е. Тамма [1] описан следующий мысленный эксперимент. Цилиндрический конденсатор помещен в однородное магнитное поле, параллельное его оси (рис.1). Если первоначально заряженный конденсатор разряжать, замыкая его обкладки проводником, то, согласно закону Ампера, на последний будет действовать сила, которая, по мнению Тамма, сообщит конденсатору угловую скорость вращения, а всей системе соответствующий момент количества движения (т. к. на магнит никакие силы не действуют, то его количество движения останется неизменным).

Увенчавшийся успехом натуральный эксперимент Грехема и Лахоза [2] аналогичен по исполнению мысленному опыту Тамма. Подавая на конденсатор переменное напряжение, регистрировали его осевые колебания (см. рис.2).

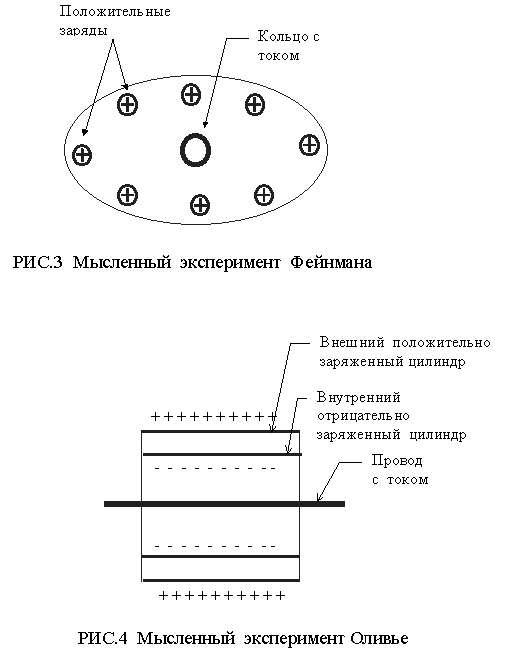
Другой способ возбуждения вращательного движения замкнутой (т.е. изолированной от воздействия внешних сил) системы рассматривает Р. Фейнман [3]. В центре диэлектрического диска прикреплено кольцо с током, а к его периферийной части “приклеены” одноименные электрические заряды (см. рис.3). При изменении величины протекающего по кольцу тока будет меняться магнитное поле, что повлечет за собой появление индуцированного кругового электрического поля, которое, воздействуя на заряды, заставит всю систему вращаться вокруг центра диска.

Случай линейного движения рассмотрел Оливье [4]. Заряженный цилиндрический конденсатор расположен вдоль оси бесконечного провода (рис. 4). При изменении тока в проводе меняется и магнитное поле вокруг него. Возбуждаемое при этом электрическое поле воздействует на конденсатор и заставляет его двигаться вдоль провода. Системы, описанные в приведенных примерах, имеют следующие отличительные особенности: 1) в них возникают активные силы (моменты сил), приложенные к вещественным элементам, вызывающие эффекты вращательного или поступательного движения. 2) не существует вещественных элементов, которые принимают на себя реакцию активных сил и обеспечивают выполнение законов сохранения импульса (момента импульса).

Отметим также, что в силу квазистационарности процессов, отсутствует излучение электромагнитных волн. (Говоря языком электротехники, есть ротор, но нет статора, в чем и состоит уникальность рассматриваемых систем.) Следовательно, должны существовать какие-то неучтенные каналы, обеспечивающие выполнение законов сохранения момента импульса (импульса) в подобных системах.

Авторы приведенных работ видят выход в том, что представления о потоке энергии (векторе Пойнтинга) и связанного с ним количества движения, справедливые по отношению к электромагнитным волнам, применимы также и к независимым друг от друга электрическим и магнитным полям (даже стационарным или медленно меняющимся). Такое количество движения известно также под названием потенциальный или статический или скрытый импульс [4]. Считается, что сумма скрытого и механического импульса (полный импульс) в замкнутых системах, аналогичных вышеприведенным, сохраняется. Тамм отмечает, что понятие электромагнитного количества движения g и потока электромагнитной энергии (вектора Пойнтинга S) было сформулировано на основе изучения переменных (в частности волновых) полей (см. [1] с. 404). Применимость этого понятия к стационарным (неволновым) полям носит характер гипотезы. Действительно, в стационарных полях эти величины обращаются в нуль ([1], с. 410).

Мнения разных авторов о способности неволновых потоков полей переносить энергию и импульс весьма противоречивы: Тамм пишет: - “общее количество движения всего статического поля по необходимости равно нулю”. Фейнман (см. [3], стр. 303) и Оливье (см. Рис.4) утверждают, что такой необходимости нет. Они приводят соответствующие примеры, согласно которым система, включающая в себя определенным образом движущиеся, по отношению друг к другу, электрические заряды с необходимостью приобретает количество движения, которое “уравновешивается” скрытым импульсом электромагнитного поля. Однако при этом получается так, что центр масс вещественных элементов системы приобретает скорость движения. С другой стороны, из-за отсутствия электромагнитного излучения, в системе нет такой эквивалентной массы, которая уносила бы импульс, противоположный импульсу ее вещественных элементов. Иными словами, нет такой массы, учет которой оставил бы центр инерции неподвижным, что, как заметил Оливье [5], несовместимо с “классическим пониманием” действия и противодействия.

Мнения Тамма и Фейнмана не расходятся лишь в оценке реальности момента импульса независимых электрического и магнитного полей. Подобной концепции придерживаются так же Грехем и Лахоз [2], авторы успешно проведенного эксперимента (см. выше). Фактически можно утверждать лишь то, что они наблюдали ту часть момента силы, которая приложена к вещественным элементам системы - это момент силы Ампера, действующий на провода, по которым течет ток заряда цилиндрического конденсатора (Рис.2)

Проанализируем опыт Грехема и Лахоза подробнее. Цилиндрический конденсатор, помещали в постоянное магнитное поле (индукция B =0,3 Тл) и на его обкладки подавали синусоидальное напряжение (E=2*10⁶ В/м с частотой f @ 240 Гц). При этом амплитуда скрытого импульса (по модулю) электромагнитных полей в элементарном объеме пространства, заключенного между обкладками конденсатора dV, будет равна 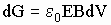, где 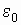- электрическая постоянная, а соответствующая амплитуда энергии (по аналогии, можно сказать "скрытой энергии") 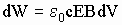, где с - скорость света (в силу соотношения между плотностью импульса и плотностью энергии электромагнитного поля [6], с.148). Плотность энергии электростатического поля заряженного конденсатора составит 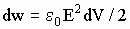. Получается так, что источник напряжения при отсутствии внешнего магнитного поля в каждом цикле заряда конденсатора на каждый элементарный объем тратит энергию dw, а при его наличии - d(W + w) т.е. в (2сB/E +1) раз больше, в данном опыте в 90 раз. Так как W и w меняются синфазно, то при включении магнитного поля во столько же раз увеличится эквивалентная емкость и возрастет ток, потребляемый установкой, а, значит, и сила Лоренца, определяющая экспериментальный результат по сравнению с расчетным, чего не могли не заметить авторы. При этом отсутствие импульсного равновесия приняло бы иную форму. Скажем также, что при наличии подобного эффекта никакая радиоаппаратура не смогла бы работать из-за сильной зависимости величин установленных в ней емкостей от ориентации по отношению к магнитному полю Земли.

В заключение рассмотрим еще один очень показательный пример. Пусть заряд q находится на расстоянии R от постоянного диэлектрического магнита сферической формы (радиус сферы -r, магнитный момент - m). Размеры заряженного тела и магнита малы, по сравнению с расстоянием между ними. Направление магнитного момента перпендикулярно прямой, соединяющей оба тела. Для определенности, в качестве магнита возьмем вращающуюся с угловой частотой w диэлектрическую сферу с равномерно распределенным по ее поверхности зарядом Q (при этом m=Qr^2w /3, см. Э. Парселл. Электричество и магнетизм. Т. 2, Изд-во “Наука”, М., 1975, с. 394). Какова величина G импульса статического (неволнового) электромагнитного поля?

Согласно Тамму (см. выше): - “... общее количество движения всего статического поля в целом по необходимости равно нулю” ([1], с. 405), что математически означает равенство нулю интеграла плотности импульса g, взятому по всему пространству, занятому статическими полями: G=o gdV=0.

Согласно Фейнману поток энергии: - “циркулирует вокруг этой системы... Это напоминает круговой поток несжимаемой воды.”. Иными словами, применительно к количеству движения всего статического поля, опять получается нулевой результат. Таким образом, нулевой результат не вызывает сомнения у обоих авторов.

Однако прямые вычисления (громоздкие, но не очень сложные, в данной статье, за неимением места, опущены) дают иное. При интегрировании плотности импульса g по всему бесконечному объему, включая внутреннюю область сферы, для абсолютной величины G получим:

G = m ₀mq/4p R² = mE/c²

где: - m ₀ - магнитная постоянная, E = q/4p e ₀R² - напряженность электрического поля заряда внутри сферы-магнита, e ₀ - электрическая постоянная.

Был вычислен и момент импульса K = m ₀mq/8p R = mER/2c². Следует отметить что, судя по литературным источникам, подобные вычисления ранее никем не производились. Видимо, только теперь очередь дошла и до них.

Векторное обобщение выглядит так: G = [Em]/ c². Результат останется справедливым, если, в качестве магнита, взять равномерно намагниченный диэлектрический шар с единичными относительными электрической и магнитной проницаемостями, при этом, плотность импульса следует определять по формуле: g = e ₀[EB], где B - вектор индукции магнитного поля (см. [3], стр.307). (Магнитные поля в обоих случаях идентичны в каждой точке пространства.) Мало того, результат вообще не зависит от формы магнита, т. к. любой объем можно представить в виде суммы сферических составляющих (главное - малость размеров). Вероятно, Тамм и Фейнман не допускали мысли о возможности ненулевого результата и, поэтому, не стали тратить времени на вычисления.

Формула для G, путем интегрирования, допускает распространение на системы, содержащие так же и протяженные заряженные и магнитные элементы. Например, импульс неволновых полей для намагниченной пластины, объемом V, на Рис. 5 по величине будет равным: G = EMV/c², что явно противоречит утверждению,

взятому из Физической энциклопедии под ред. А. М. Прохорова (М., 1998, т.2 , с.131): - “В статич. эл.-магн. полях сосредоточенных в ограниченном объеме, И. э. п. (импульс электромагнитного поля) всегда равен нулю ...”.

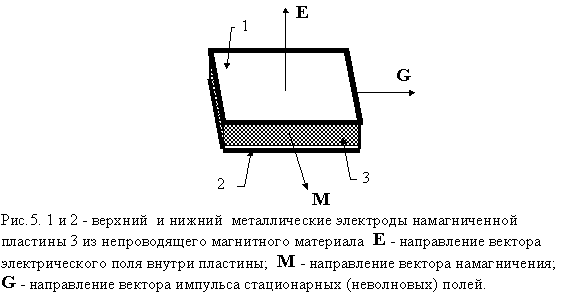
Таким образом, согласно прямым вычислениям, величина, именуемая скрытым импульсом, электромагнитных полей, вопреки общепринятой концепции, в общем случае, не равна нулю (G=o gdV? 0). Однако ее отождествление с импульсом (плотностью импульса) равносильно признанию возможности изменения скорости центра инерции замкнутой системы, что несовместимо с современными представлениями о законе сохранения импульса. Кроме того, в обычных волновых электромагнитных полях импульс и связанная с ним энергия W = cG распространяются со скоростью света, тогда как в волновых они “стоят” на месте, что выглядит так же противоестественно, как “покоящиеся фотоны”. Предложение Оливье считать эти величины “потенциальными” тоже не “работает”, т. к., по аналогии с вышеприведенными соображениями (см. анализ опыта Грехема и Лахоза), вышеуказанная энергия (W = cG) должна была бы войти в выражение для полной энергии статических полей в качестве нового невиданного члена и обусловить появление столь же невиданных и никогда не наблюдаемых эффектов. Например, величина емкости плоского конденсатора, изображенного на Рис. 5, испытывала бы многократные изменения в зависимости от величины намагниченности его сердечника (пластины из непроводящего магнитного материала). Этот явный абсурд указывает на полную несостоятельность переноса представлений об импульсе и энергии с волновых полей на неволновые.

Тот факт, что сумма механического момента импульса K_M и момента скрытого импульса неволновых полей, K, в опытах Тамма и Грехема и Лахоза сохраняется , d(K + K_M)/dt = 0 (см. [1], с. 407), на самом деле, не носит универсальный характер, вследствие чего, не имеет ничего общего с законом сохранения момента количества движения. Это обусловлено характером полей точечного электрического заряда и точечного магнитного диполя и распространяется на системы, содержащие протяженные заряженные и магнитные элементы, в силу принципа суперпозиции. Приведенное выражение, в общем случае, зависит от конфигурации системы. Оно справедливо только при изменении электрического поля в постоянном магнитном (как в опытах Тамма, Грехема и Лахоза) и нарушается при изменении последнего. Например, используя, вышеприведенные результаты, можно показать, что, при условии малости размеров кольца с током, по сравнению с расстоянием до зарядов, в опыте Фейнмана (Рис. 3) dK_M/dt по абсолютной величине в два раза превышает dK/dt, в связи с чем, объяснение, данное Фейнманом, основанное на их равенстве [3, с. 304], не имеет места (в чем можно убедиться путем прямых вычислений). Это еще раз указывает на отличие К и dK/dt от момента импульса и момента силы, соответственно. Таким образом, реальные эффекты, описываемые в мысленных экспериментах Фейнмана и Тамма и нашедшие экспериментальное подтверждение в опытах Грехема и Лахоза, не имеют объяснений с позиции всей совокупности знаний, имеющихся в современной физической науке.

Вместе с тем, можно констатировать следующий факт: системы, показанные на Рис. 1,2,3 совершают движение под действием моментов сил Лоренца (Ампера) (Рис. 1,2) или индукции (Рис. 3), по отношению к которым не существует противодействия как со стороны вещественных, так и полевых элементов, входящих в них. Следовательно, эти моменты сил являются не внутренними, а внешними по отношению к системе, которая, вопреки первоначальным посылкам, фактически оказывается не замкнутой. Приведенное утверждение, по существу, представляет собой содержание нового экспериментально подтвержденного самодостаточного закона природы.

Вывод о не замкнутости рассматриваемой системы свидетельствует о неполноте современных критериев замкнутости и диктует необходимость их пересмотра.

Так же возникает вопрос о существовании видов материальных структур не вещественной и не полевой природы, с которыми вступают в силовое взаимодействие вещественные элементы данных систем.

ВЫВОДЫ

1. Согласно приведенным литературным источникам, существуют системы, содержащие электрически заряженные и магнитные элементы, в которых при изменении электрических или магнитных полей в квазистационарном режиме (при этом практически отсутствует излучение электромагнитных волн) возникают силы Ампера или силы индукции, не уравновешивающиеся силами реакции, действующими со стороны вещественных элементов системы. При этом системы (точнее, совокупность всех вещественных элементов систем) способны совершать вращательное или поступательное движение, приобретая механический момент импульса (импульс). По мнению авторов упомянутых лит. источников, изменение механического момента импульса соответствует такому изменению момента импульса стационарных (квазистационарных) полей, при котором обеспечивается выполнение закона сохранения общего (вещество + поле) момента количества движения рассматриваемой замкнутой системы.
2. Прямые вычисления, “общего количества движения всего статического поля в целом”, для системы точечный электрический заряд - точечный магнитный диполь (“точечный” - в смысле малости размеров объектов по сравнению с расстоянием между ними), дают возможность точного определения этой величины для систем содержащих протяженные заряженные и магнитные элементы сложной формы (путем интегрирования). Неожиданно для сторонников концепции применимости к стационарным полям представлений о векторе Пойнтинга и импульсе электромагнитного поля, справедливых по отношению к волновым полям, получен ненулевой результат (И. Е. Тамм [1], с. 405; Р. Фейнман [3], с. 304; Физическая энциклопедия под ред. А. М. Прохорова, М., 1998, т.2 , с.131).
3. На основании п. 2, трактовка соотношения , dK_M/dt = -dK/dt ((см. [1], с. 407), где K - момент импульса стационарных полей (момент скрытого импульса), K_M - механический момент импульса), как закона сохранения момента импульса замкнутых систем при наличии стационарных полей, является ошибочной т. к. оно (соотношение) не выполняется при изменении магнитного поля. Например, при условии малости размеров кольца с током, по сравнению с расстоянием до зарядов, в мысленном эксперименте Фейнмана (Рис. 3) dK_M/dt по абсолютной величине в два раза превышает dK/dt (в чем нетрудно убедиться путем прямых вычислений), в связи с чем основанное на их равенстве объяснение, данное Фейнманом, так же не имеет места. Представление о векторе Пойнтинга как об импульсе стационарных полей влечет за собой так же предсказание ряда не существующих эффектов, которые были бы зарегистрированы в опытах Грехема и Лахоза и др. способами. Таким образом, сложившаяся ситуация требует отказа от понимания величины, именуемой моментом импульса (скрытого импульса) стационарных (квазистационарных) полей как от фактора обеспечения импульсного (силового) равновесия замкнутых систем.
4. Выводы по п. п. 1,2,3 позволяют сформулировать следующее заключение. В замкнутых (по традиционным представлениям) системах, содержащих электрически заряженные и магнитные элементы, в процессе изменения электрических и магнитных полей в квазистационарном режиме, возникают моменты сил (Лоренца или индукции), по отношению к которым отсутствуют ответные моменты сил реакции со стороны как вещественных, так и полевых видов материи входящих в эти системы. Приведенное заключение, по существу, представляет собой формулировку нового самодостаточного экспериментально подтвержденного, закона природы.

1. В связи с тем, что моменты сил по п. 4 не уравновешиваются моментами сил реакции, они являются не внутренними, а внешними по отношению к системе, которая, вопреки первоначальным посылкам, фактически оказывается не замкнутой, что свидетельствует о неполноте принятых критериев замкнутости систем. Факторы, обеспечивающие при этом импульсное (силовое) равновесие и энергетический баланс, связаны с существованием неизвестной разновидности материи не вещественной и не полевой природы.

ЛИТЕРАТУРА

1. И.Е.Тамм. Основы теории электричества. Издательство технико-теоретической литературы, М.,”НАУКА”, 1989, с. 404-408, 411, 241
2. G.M.Graham, D.G.Lahoz. Nature, 285, 154, 1980.

1. Фейнман, Лейтон, Сэндс. Фейнмановские лекции по физике, т.6, изд-во “Мир”, 1977, стр. 59, 304.

1. Costa de Beauregard Olivier. C. r. Acad. Sci. 263, No23, B1279, 1966. (РЖФ, 1967, 5Б85).
2. Costa de Beauregard Olivier. C. r. Acad. Sci. 260, No25, 6546-6549, 1965. (РЖФ, 1965, 8Б141).

1. Л Д. Ландау, Е. М. Лифшиц. Теория поля. Изд-во “Наука”, М., 1973, с. 70, 265-266.

Дата публикации: 9 августа 2001
Источник: SciTecLibrary.ru

Размещено на сайте 08.02.2016.

Статьи других авторов
На главную