Классическая электродинамика выходит на новые рубежи. На основании её законов установлена теорема о существовании сил, условно названных безреактивными (безопорными), эффекты действия которых уже имеют экспериментальное подтверждение. Подробная информация дана на сайте <http://www.tts.lt/~nara >. Оказывается, безреактивные силы есть разновидность давно известных сил Ампера (Лоренца). Статья построена таким образом, чтобы, несмотря на тесную логическую связь с материалами, изложенными на сайте, могла восприниматься как самостоятельная работа.
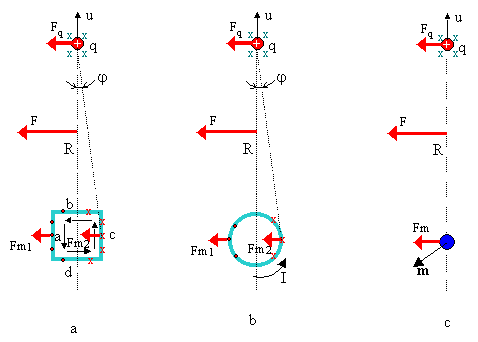
На рис. 1 а изображена квадратная рамка со сторонами a, b c, d, по которой течёт ток I, в направлении, указанном стрелками. На расстоянии R от центра рамки в направлении указанном стрелкой, движется (для определённости положительный) электрический заряд q со скоростью u.

Рис. 1. Fm1, Fm2 - силы, действующие на части контуров с током I, Fm - сила, действующая на весь токовый элемент (рамку или магнитный диполь), F - равнодействующая сила, q - электрический заряд, R - расстояние между зарядами и токовыми элементами, m - магнитный момент, a, b, c, d - равные между собой стороны квадратного контура.
Примем размеры рамки настолько малыми, по сравнению с расстоянием R, чтобы магнитное поле вдоль сторон a и c можно было считать неизменным. Задача состоит в том, чтобы определить равнодействующую всех сил в системе рамка - заряд. Движение заряда будет возбуждать во всём пространстве магнитное поле, индукцию которого можно определить по закону Био и Савара.
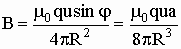 (1)
(1)
j - угол между вектором скорости и радиус-вектором от заряда до точки наблюдения, из рисунка видно, что sinj = b/2R =a/2R.
Силовые линии В будут описывать окружности около линии движения заряда (по часовой стрелке), проходя через сторону квадрата с как бы "вглубь" чертежа (обозначено красными крестиками) и выходя из стороны а, в обратном направлении (обозначено красными кружочками). Таким образом, по сторонам а и с текут противоположные токи в противоположных магнитных полях, значит, действующие на них силы Ампера будут одинаковыми (по величине и направлению): Fm1 = Fm2. Так как силы, действующие на стороны b и d уравновешивают друг друга, то сила Ампера Fm, действующая на всю рамку будет равна:
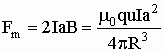
Учитывая, что магнитный момент рамки m = Ia2, получим:
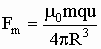 (2)
(2)
Где m - магнитный момент рамки с током.
Для определения равнодействующей всей системы необходимо ещё вычислить силу Fq, действующую на движущийся заряд - силу Лоренца: Fq = quBm
Bm- индукция создаваемого рамкой с током магнитного поля, в точке нахождения заряда q, Bm = m 0m/4p R3. Отсюда получим:
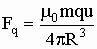 (3)
(3)
Сравнивая (2) и (3) заметим (не без удивления) что силы Fm и Fq равны между собой, причём не только по величине, но и по направлению, в чём легко убедиться, применяя правило левой руки. Отсюда равнодействующая системы будет равна:
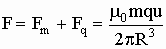 (4)
(4)
Если взять не квадратный, а круговой (см. Рис. 2 b) контур и проделать аналогичный расчёт (вычислив несложный интеграл), получим полное совпадение с формулой (4). Оно и понятно - играет роль не форма контура, а входящий в формулу магнитный момент роль которого может выполнять любой токовый магнитный диполь, кусочек намагниченного вещества, атом, ядро, электрон, нейтрон и т. д. (см. Рис. 2 c). И всё это - чистая сила Ампера! Преобразуем (4) к другому виду. Для этого обратим внимание на то, что движение заряда вызывает во всём пространстве сопутствующий ток смещения j, равный скорости изменения вектора электрической индукции. Вычисление j в точке расположения магнитного диполя даёт следующий результат: j = e 0qu/2p R3. Подставляя в (4), получим: F = m 0mj или, в другой форме:
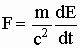 (5)
(5)
В словесной формулировке (5) "выглядит" так: - " Равнодействующая сила системы заряд - магнитный диполь, равная по величине сумме силы Ампера действующей на магнитный диполь со стороны возбуждаемого движущимся зарядом магнитного поля и силы Лоренца, действующей на заряд, движущийся в магнитном поле магнитного диполя, вычисляется как произведение магнитного момента на скорость изменения электрического поля, поделённое на квадрат скорости света". Речь идёт именно о той силе, которая на сайте условно названа безреактивной или размыкающей (превращает систему из замкнутой в незамкнутую).
Сила, действующая на магнитные диполи малых размеров (атомы, ядра, электроны), которые при расчётах часто принимают за точечные объекты, уже теряет видимое сходство с силой Ампера. Назовём её - скрытая сила Ампера.
Как поведёт себя рассматриваемая система при изменении магнитного момента магнитного диполя? Чтобы не усложнять расчеты, будем придерживаться таких ограничений, при которых можно пренебречь влиянием того волнового излучения, которое при этом появится, т. е. расстояние R должно быть малым по сравнению с длиной волны, что соответствует достаточно малым частотам изменения магнитного момента. Такое изменение вызовет действующую на заряд силу индукции.
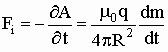
A - величина векторного потенциала, создаваемого магнитным диполем, в точке размещения заряда.
Одновременно возникнет приложенная к магнитному диполю, так называемая, магнитодинамическая сила
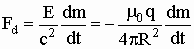
(см., например, D. G. Lahoz, G. M. Graham. Can. J. Phys. Vol. 57, 1979, s. 667 или Л. Д. Ландау, Е. М. Лифшиц. Электродинамика сплошных сред. М., 1957, с., 307), равная по величине противоположная по направлению силе индукции, что не повлияет на результирующую системы (см. также сайт, "Академический вариант", Часть 3, где эта формула получена другим способом).
Таким образом, магнитный момент в формуле (5) можно считать переменной величиной.
Из (5) видно, что синхронное (синфазное или противофазное) изменение магнитного момента и скорости изменения напряжённости электрического поля (проще говоря, тока смещения) даст постоянную по направлению безреактивную силу, появление которой наглядно отображено на рисунке 2.
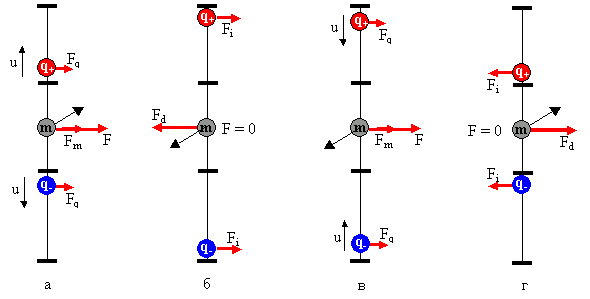
Рис. 2. Возникновение безреактивной силы в пошаговом процессе.
В середине твёрдого тонкого стержня укреплён шарик из магнитного диэлектрического материала, который, при желании, можно перемагничивать. Вдоль длины стержня между ограничителями (показаны жирными короткими линиями) могут перемещаться электрические заряды. Начальное состояние (Рис. 2 а): - шарик намагничен (направление магнитного момента пронизывает плоскость чертежа от читателя, силовые линии магнитного поля пронизывают области расположения зарядов, наоборот, в направлении от плоскости чертежа к читателю).
На первом шаге (Рис.1 а) заряды начинают движение от внутренних ограничителей к внешним с равными скоростями u. На каждый из них будет действовать сила Лоренца Fq, а на магнитный диполь скрытая сила Ампера Fm. Направления одинаковы. В результате суммирования получится равнодействующая безреактивная сила F, которая будет сохраняться до тех пор, пока заряды не достигнут внешних ограничителей. Если система находится в свободном пространстве, то она приобретёт ускоренное движение и получит приращение скорости.
На втором шаге (Рис. 2 б) заряды упрутся в верхние ограничители. Рассмотренные силы Fq и Fm , действовать перестанут. Ускоренное движение прекратится. Начнётся перемагничивание (изменение направления намагничения) магнитного диполя, что приведёт к появлению во всём пространстве индукционного электрического поля и воздействию на положительный и отрицательный заряды одинаковых по величине и направлению сил Fi, которые обе будут уравновешены противоположно направленной магнитодинамической силой Fd, действующей на меняющий свой магнитный момент магнитный диполь в электрическом поле зарядов. Таким образом, до завершения процесса перемагничивания равнодействующая будет сохранять нулевую величину, а система продолжит движение без ускорения с той скоростью, которой она достигла в конце первого шага.
На третьем шаге (Рис. 2 в) перемагничивание завершится. Магнитный момент приобретёт величину, противоположную той, которую он имел на первом шаге. Заряды начнут движение от внешних ограничителей к внутренним навстречу друг другу, т. е. с противоположными, по отношению к первому шагу, скоростями. В результате, возобновится безреактивная равнодействующая сила по величине и направлению совпадающая с той, которая была на первом шаге. Таким образом, система продолжит ускоренное движение в прежнем направлении и в конце третьего шага удвоит ту скорость, которую приобрела в конце первого.
Четвёртый шаг (Рис. 2 г) аналогичен второму с той разницей, что заряды упрутся не во внешние, а во внутренние ограничители. Индукционные и магнитодинамическая силы при перемагничивании будут противоположны тем, которые были на втором шаге, а их сумма останется равной нулю. Система будет двигаться по инерции со скоростью, достигнутой в конце третьего шага, до тех пор, пока заряды опять не упрутся во внешние ограничители. Далее будут повторяться четырёхшаговые циклы, ничем не отличающиеся от рассмотренного. Таким образом, с каждым циклом скорость будет возрастать и может достигнуть любой величины, ограниченной лишь скоростью света.
Теперь рассмотрим устройство, изображённое на Рис. 3. Цилиндрический сердечник из магнитного диэлектрического материала может перемагничиваться изменением тока, протекающего через соленоид. На внутренний и внешний электроды подаётся переменное напряжение. Заметим, что данное устройство, образующее своеобразный цилиндрический конденсатор, можно рассматривать как комбинацию из множества элементарных ячеек, изображённых на Рис. 2. Роль ограничителей выполняют обкладки конденсатора. Принцип работы аналогичен. Рассмотренный нами пошаговый режим хорош для наглядности, но в техническом отношении неудобен. В этом и нет особой необходимости.
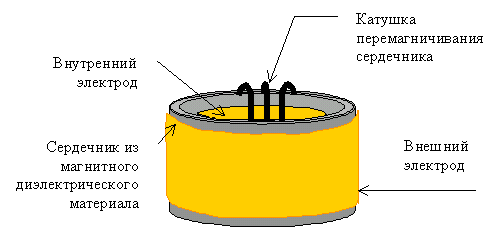
Рис. 3. Схема устройства, способного совершать неограниченное в пространстве (инфинитное) движение за счёт создаваемой в нём безреактивной силы
Если на электроды подавать такое напряжение, чтобы напряжённость электрического поля в сердечнике менялось, например, по закону E = E0wsin t, а на катушку такой ток, чтобы намагниченность менялась по закону M = M0wcos t, то на устройство вдоль оси цилиндра будет действовать постоянная по направлению безреактивная сила, со средней величиной Fср fEp= 0M0V/c2, где E0, M0 - амплитуды величин напряжённости электрического поля и намагниченности сердечника, f - частота, V - объём сердечника. В результате, устройство сможет либо ускоренно двигаться, либо совершать работу против внешних сил ( см. также Г. П. Иванов, Ю. Г. Иванов. Способ получения тяги. Патент РФ № 2172865, М., 2001 г.). Рассматриваемый режим работы установится автоматически, если на ячейку подавать питание согласно эквивалентной схеме, изображённой на Рис. 3.
Сделаем ещё одно преобразование. Возьмём уравнение Максвелла rot H = j (j - плотность тока смещения в вакууме). Тогда уравнение (5), после перехода к векторной форме, можно записать в виде:
F = m 0[m rot H] = [m rot B] (6)
А теперь самое интересное! В тридцатых годах в науке бурно бушевали споры о природе магнитного момента элементарных частиц. Одни (Ю. Швингер) утверждали, что это токовый магнитный момент, другие (Ф. Блох) доказывали , что "монопольный" - дескать, дипольный момент образуют противоположно заряженные магнитные монополи. Спор разрешили К. Г. Шал (C. G. Shull) и др. в 1951 году в экспериментах по рассеянию нейтронов в неоднородном магнитном поле (см. Физическая энциклопедия под ред. Прохорова и др. М., 1998, т. 5, с. 522 (2). Статья "Электродинамика".). Дело в том, что в вихревом магнитном поле "монопольные" диполи не испытывали бы никаких сил, в отличие от токовых, на которые должна действовать сила, численно равная нашей безреактивной силе (правая часть формулы (6)). Эксперименты подтвердили токовую концепцию! Значит магнитный момент нейтрона, а, следовательно, и всех остальных элементарных частиц имеет токовую природу.
Но взглянём на дело по другому. Сами того не подозревая, эти уважаемые экспериментаторы измерили безреактивную силу Амперовой природы. Иными словами они на уровне элементарных частиц экспериментально подтвердили ту концепцию безреактивных сил, которую мы доказали на макроскопическом уровне.
Энергетические аспекты безреактивного движения подробно рассмотрены на упомянутом сайте.
Дата публикации: 23 апреля 2002
Источник: SciTecLibrary.ru
Размещено на сайте 08.02.2016.
Статьи других авторов
На главную