ТАКОВО МНЕНИЕ МАГНИТОДИНАМИЧЕСКОЙ СИЛЫ

© Георгий Петрович Иванов

Написать автору: nara@tts.lt

Новая сущность классической электродинамики, связанная с "безреактивными" силами и "разомкнутыми" системами (см. сайт http://www.tts.lt/~nara ) требует более пристального рассмотрения некоторых важных, но явно обделённых вниманием величин, таких, например, как, так называемая, магнитодинамическая сила, родственница силы Лоренца.

Эта сила дуальна (получается заменой электрических характеристик на магнитные и наоборот) по отношению к силе Лоренца, F_L. Действительно,

F_L = q[uB] = [(дp/дt)B]          (1)

где: q - электрический заряд, u - скорость движения заряда, B - индукция магнитного поля, дp/дt - скорость изменения электрического дипольного момента. Заменяя электрический дипольный момент p на магнитный момент m, а индукцию магнитного поля на напряжённость электрического поля E и, меняя знак векторного произведения получим:

F_m = [E(дm/дt)]/c²          (2)

где F_m и есть та самая магнитодинамическая сила, c - скорость света. В аналогичном виде она дана в [1], а в [2] входит в уравнение для объёмной плотности силы в при наличии переменного электромагнитного поля в диэлектрической среде.

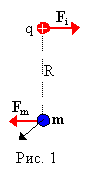
Таким образом, согласно классическим представлениям, магнитодинамическая сила действует на меняющийся магнитный диполь, помещённый в электрическое поле. На рис. 1 изображена система содержащая электрический заряд (для определённости положительный) и токовый магнитный диполь. Положим, что размеры частиц малы по сравнению с расстоянием между ними и что они неподвижны относительно друг друга. Пусть величина магнитного момента возрастает в направлении, указанном стрелкой (перпендикулярном к R). Величина и направление возникшей при этом магнитодинамической силы будет определяться по формуле (2). Электрическое поле, создаваемое зарядом в области, занимаемой магнитным диполем, можно представить в виде: E = - qR/4p e ₀R³ (знак минус указывает на то, что расстояние отсчитывается от магнитного диполя). Подставляя в (2), учитывая, что с² = 1/e ₀m ₀, получим:

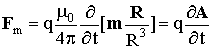       (3)

где А - векторный потенциал, создаваемый меняющимся магнитным диполем в области, занимаемой электрическим зарядом.

С другой стороны, изменение магнитного момента магнитного диполя сопровождается появлением во всём пространстве электрического поля индукции E_i, что вызовет действие на заряд силы индукции F_i = -q(дA/дt) см. [3] . Сравнивая с (3), видим, что

F_m = -F_i        (4)

или F_m + F_i = 0.

Полученный результат можно сформулировать так: магнитодинамическая сила, испытываемая меняющимся магнитным диполем, помещённым в электрическое поле, создаваемое зарядом, равна по величине и противоположна по направлению той силе индукции, которую испытывает заряд, в индукционном электрическом поле, возбуждаемом меняющимся магнитным диполем.

Таким образом, магнитодинамическая сила обеспечивает выполнение закона сохранения количества движения и замкнутость системы при изменении магнитного момента магнитного диполя.

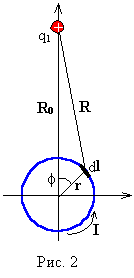
Пусть роль магнитного диполя выполняет изображённый на рис. 2 круговой контур с током I. В этом случае, изменение магнитного момента контура является следствием изменения тока в нём, дm/дt = p r²дI/дt. Магнитодинамическую силу, испытываемую всем контуром, можно представить как результат интегрирования, сил действующих на элементы длины дуги. Из (4) следует, что

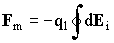;       (5)

где - dE_i - сила индукции, создаваемая элементом контура.

Дифференцируя (5), получим:

dF_m = -qdE_i        (6)

Выражение для dE_i можно записать в виде (см. [3])

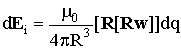;       (7)

где dq - заряд, движущийся с ускорением w по элементу длины дуги контура dl (Рис. 2), R - расстояние между зарядом q₁ и dq. Отметим, что dqw = (дI/дt)dl , где дI/дt - скорость изменения тока в контуре.

Переобозначив в (6) и (7) dq через q, dF_m через F_m, получим:

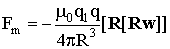       (8)

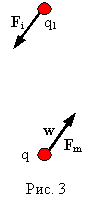
Формула (8) поясняется рисунком 3. Она описывает магнитодинамическую силу F_m, которую испытывает заряд q, движущийся с произвольным ускорением, со скоростью, малой, по сравнению со скоростью света со стороны неподвижного заряда q₁ (R - расстояние между зарядами). Ускоренное движение заряда q будет возбуждать во всём пространстве электрическое поле индукции, которая воздействует на заряд q₁ с силой F_i, в соответствии с (6), равной по величине и противоположной по направлению F_m.

Таким образом формула (4) F_m = -F_i, справедлива как по отношению к меняющемуся магнитному диполю, так и по отношению к ускоренно движущемуся заряду. Магнитодинамическая сила обеспечивает выполнение закона сохранения количества движения и замкнутость системы в обоих случаях., что наглядно представлено на рисунке 4

.

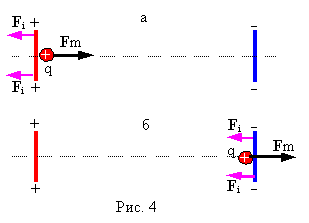
Заряд q содержится в устройстве, в котором он совершает возвратно-поступательное движение между двумя противоположно заряженными пластинами. Примем скорость заряда между пластинами равномерной, кроме областей непосредственно примыкающих к их поверхностям, где заряд поворачивает, испытывая ускоренное (замедленное) движение, вследствие чего его скорость меняется на противоположную. Из рисунка видно, что возникающие на поворотах силы индукции (см. рис. 4а, б), действуют на обе пластины в одном и том же направлении. Равновесие обеспечивают равные по величине и противоположные по направлению магнитодинамические силы, без которых система совершала бы инфинитное (неограниченное в пространстве) ускоренное движение под действием одних только сил индукции.

В случае системы из двух зарядов, как на Рис. 3, силы F_i и F_m образуют пару, момент которой M можно найти, векторно умножая на R обе части уравнения (8). Получим:

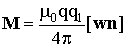      (9)

где n = R/R - единичный вектор вдоль направления радиус-вектора от ускоренно движущегося заряда q к заряду q₁. Отметим, что согласно простой красивой формуле (9), момент силы замкнутой по традиционным критериям системы двух зарядов, один из которых движется ускоренно не зависит от расстояния между зарядами, а определяется только величиной и направлением ускорения. Если бы мы ничего не знали о существовании разомкнутых систем, которые подробно рассмотрены в упомянутом в начале статьи сайте и в брошюре [4], то, вероятно, получили бы шок от внезапного осознания нарушения закона сохранения момента количества движения. Не нашлось бы ни малейшей спасительной соломинки, за которую можно было схватиться. Пасует даже электромагнитное излучение ускоренно движущегося заряда, ведь оно не зависит от входящего в формулу (9) покоящегося заряда q₁. Но нам известно (из сайта или из [4]) что рассматриваемая система относится к одному из видов разомкнутых систем, в силу чего, нарушение закона сохранения момента импульса чисто иллюзорное и что, следует учитывать взаимодействие с электровакуумом, одной из структурных составляющих физического вакуума (или, если угодно, релятивистского электромагнитного эфира, удовлетворяющего принципу относительности, по крайней мере, в Галилеевской формулировке, всегда справедливой для малых скоростей). Тогда все фундаментальные законы сохранения остаются первозданно справедливыми.

Применение формулы (9) к изображённой на Рис. 2 системе заряд - круговой контур с током, даёт:

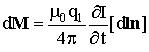      (10)

где dM - момент пары сил , приложенных к заряду q₁ и к элементу длины дуги dl, дI/дt - скорость изменения тока в контуре. Каждому единичному вектору соответствуют две лежащие на окружности точки, в которых величины векторных произведений dlnsina (где a - угол между векторами dl и n) равны по величине и противоположны по направлению, из за того, что углы a отсчитываются от разных сторон n. Отсюда, для каждого направления n, моменты сил попарно уничтожаются dM = 0, а, значит, и M = 0. Тот же результат даёт непосредственное интегрирование по контуру.

Таким образом, полный момент силы в системе, содержащей заряд и токовый магнитный диполь (Рис. 1, 2), возникающий при изменении магнитного момента равен нулю. Магнитодинамическая сила обеспечивает не только выполнение закона сохранения импульса, как уже рассмотрено выше (Рис. 1) но и момента импульса, что делает систему замкнутой, в общепринятом смысле этого слова.

Теперь самое время вновь вернуться к рассмотрению мысленного эксперимента Р. Фейнмана, изложенного в [5] и на сайте <http://www.tts.lt/~nara/history/feynman.html >.

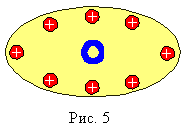
Кратко напомним. К периферии диска (Рис. 5) прикреплены электрические заряды, а к центру сверхпроводящее кольцо с током. Окружающая температура повышается до тех пор, пока не исчезнет сверхпроводимость. Исчезновение тока вызовет действующее на заряды индукционное электрическое поле. По утверждению Р. Фейнмана диск начнёт вращаться. Согласно вышеприведённому рассмотрению диск останется на месте т. к. не учтённый Р. Фейнманом момент магнитодинамической силы, приложенный к кольцу с током уравновесит действие моментов сил индукции, приложенных к зарядам. "Диск - замкнутая по моменту количества движения система. Он будет стоять." - таково мнение магнитодинамической силы, а с ней не поспоришь, стихия природы. Зарядам, ускоренно (замедленно) движущимся внутри кольца (из за чего ток в кольце меняется) "кажется" будто относительно них ускоренно движутся периферийные заряды, на самом деле, покоящиеся, по отношению к наблюдателю, находящемуся в лабораторной системе отсчёта. Возникающая при этом "кажущаяся" сила индукции и есть та самая таинственная магнитодинамическая сила, о которой мы говорим. Это образное представление помогает лучше понять физический смысл магнитодинамической силы. Её влияние следует учитывать во всех процессах, сопровождающихся изменением электрического и магнитного состояния в разнообразных физических системах как на микро, так и на макро уровнях.

Рассмотренная ситуация показывает, что классическая электродинамика отнюдь не является образцом законченной науки, вопреки расхожему мнению ортодоксально настроенных релятивистов. В ней ещё остались белые пятна.

ЛИТЕРАТУРА:

1. D.G.Lahoz, G.M.Graham. Can. J. Phys., 57, No5, 1979, p.667-676.
2. Л. Д. Ландау и Е. М. Лифшиц. Электродинамика сплошных сред. М., 1973, с. 307.
3. Л. Д. Ландау, Е. М. Лифшиц. Теория поля. М., 1973, с. 211, 212.
4. Иванов Г. П. Классическая электродинамика и современность, Висагинас (Литва), 2002.
5. Фейнман, Лейтон, Сэндс. Фейнмановские лекции по физике, т.6, изд-во “Мир”, 1977, стр. 59, 304.

Дата публикации: 13 мая 2002
Источник: SciTecLibrary.ru

Размещено на сайте 10.02.2016.

Статьи других авторов
На главную