БЕЗОПОРНОЕ ДВИЖЕНИЕ И ГРАВИТАЦИОННАЯ ЭНЕРГЕТИКА: ТЕОРИЯ И ЭКСПЕРИМЕНТЫ, ПОДТВЕРЖДАЮЩИЕ ИХ РЕАЛЬНОСТЬ

  © Петров А.М.

Контакт с автором: petrov700@gmail.com

  Отечественная наука в опасности! Не от плохого финансирования, которое руководство РАН хотело бы утроить, чтобы решить все свои проблемы. А от фактического её превращения в лженауку, которая и с утроенным бюджетом, при сложившейся клановой замкнутости, моральной деградации и прогрессирующем непрофессионализме, может стать только трижды лженаукой!

Руководство РАН “отвлекает внимание и заметает следы”

20 мая 2011 года вице-президент Российской академии наук (РАН) Александр Некипелов, выступая перед журналистами, заявил, что Российской науке необходимо срочное вливание как минимум 15-ти миллиардов рублей. В противном случае долго она не протянет. Действительно, вклад российских учёных в мировую науку сегодня составляет только 2%. Такие данные ещё в 2010 году привёл главный учёный секретарь президиума РАН академик Валерий Костюк. По его словам, аналогичный показатель США составляет 35%. Как отметил учёный, число научных специалистов в России постоянно сокращается, тогда как в развитых странах мира оно растёт. Как отмечает Костюк, в США, странах ЕС и Китае учёных за последнее десятилетие стало больше в разы. Одной из причин сложившейся ситуации он назвал недостаток финансирования, которое выделяют в три раза меньше необходимого. В настоящий момент бюджет Академии наук составляет 49 млрд рублей, из которых 31,5 приходится на центральную часть и 17,5 млрд – на региональные отделения. (из статьи “Учёные выдвинули властям ультиматум” в ежедневной электронной газете "Утро.ru").

( http://www.utro.ru/articles/2011/05/20/975491.shtml).

А 23 мая 2011 года Президент страны Дмитрий Медведев провёл беседу с группой российских и зарубежных учёных, получивших гранты на научные проекты в России. На какие же цели планируют они расходовать полученные средства, что поддерживать, а чему противодействовать? Относительно последнего чётко высказался профессор Аризонского университета США, академик РАН Владимир Захаров. Вот его видение ситуации в российской науке:　"В России развилась антинаука. В космосе летает гравицапа, которая отрицает закон сохранения импульса, и на это потрачены большие деньги".

Далее предоставим слово освещавшему встречу корреспонденту:

“Гравицапа – неодушевленный предмет и не может ничего отрицать – ни закона сохранения импульса, ни того, что дважды два четыре. Если бы поэт Захаров понимал, что на приёме у президента надо говорить исключительно по делу, то он бы выразился примерно так: работа гравицапы основана на физических законах, о которых наша РАН ничего не знает и даже не догадывается. Но тогда было бы совершенно непонятно, чем перед Захаровым провинилась гравицапа. Грамотный в физике человек наверняка знает, что эксперимент в этой науке намного важнее, чем физическая теория, и если эксперимент опровергает теорию, то выбрасывают теорию, а не результаты эксперимента. Во всяком случае, именно так должно быть в нормальной науке. Если гравицапа летает, то этого уже вполне достаточно, чтобы не делать из неё заклятого врага российской науки. В этом смысле стенания нашего поэта, академика и американского профессора Захарова – пустое сотрясение воздуха и больше ничего. Нет никаких оснований считать создателей гравицапы лжеучёными, и наверняка в РАН об этом знают, но помалкивают… ждут, как дело обернётся. А так и обернулось – Захаров опозорил и РАН, и всю российскую науку перед президентом. Если президент об этом пока не догадывается, то это не должно никого сильно успокаивать.

Теперь поговорим о том, сколько денег потрачено на гравицапу. Это очень важно, потому что поэт Захаров уделяет этому вопросу особое внимание. Он сказал, что на неё потрачены большие деньги. Лично мне неизвестно, какие деньги Захаров считает большими. Поэтому давайте я вам сразу напишу, что денег из российского бюджета на гравицапу не выделялось ни копейки, и все работы по её созданию велись на чистом энтузиазме. Как, по-вашему, ноль – это очень большие деньги? И какое вообще дело американскому аризонскому профессору до того, что несколько человек на свои личные сбережения построили гравицапу? Пусть учится считать деньги в своём кармане, такое умение в скором времени может очень сильно пригодиться.

У Захарова в одной коротенькой фразе о гравицапе столько накручено лжи и самой обыкновенной невежественности, что с трудом верится, что это говорил академик. Именно поэтому лично я предпочитаю называть его поэтом. Но даже и поэты раньше стеснялись произносить такие речи” (Андрей Воробьев. Источник:　newsland.ru)

http://newsland.ru/News/Detail/id/707062/

Руководство РАН “эксплуатирует” данную тему не первый раз. В октябре 2008 года корреспондент газеты “Аргументы и факты” писал:

“Валерий Александрович (Меньшиков, директор НИИ космических систем) показал мне письмо академика-секретаря отделения энергетики, машиностроения, механики и процессов управления РАН В.Фортова руководству Федерального космического агентства. Уважаемый учёный, один из самых авторитетных физиков страны, уверяет, что эксперимент в космосе с включением нового двигателя нанесёт ущерб престижу России и репутации отечественной науки, поскольку принцип работы двигателя противоречит основополагающим законам механики и пытается реализовать антинаучную идею. Опасения академика были бы понятны, если бы эксперимент потребовал специальных финансовых затрат или угрожал существованию спутника. Но двигатель можно включить после выполнения спутником своих главных задач. Тяга величиной 28　граммов не представляет опасности для спутника. Затрат на эксперимент также не предвидится: двигатель уже установлен на борту и даже электричество для его работы даровое — от Солнца. Поэтому всякий риск исключён. И престиж науки не пострадает: если двигатель не заработает, учёные убедятся, что он неработоспособен; если заработает, реализован новый принцип движения. А то, что теория отстаёт от практики, не страшно — так бывало в науке не раз”

(АИФ №41 от 08 октября 2008. Савелий Кашницкий. В космос без топлива. На орбиту выведен “вечный” двигатель).

http://www.trinitas.ru/rus/doc/0231/007a/02311016.htm

Несомненно, последний демарш академика РАН перед Президентом страны имеет целью отвлечь внимание от другого, действительно весьма дорогостоящего, проекта, ответственность за неизбежный срыв которого перед руководством страны и перед научной общественностью ещё предстоит нести нынешнему руководству РАН, почему оно и пытается любыми путями отсрочить начало объективного разбирательства по этому делу. Что же это за проект? Процитируем (с незначительными сокращениями) главу “Сто дырок от бублика” из публикации физика Бориса Осадина “ТОКАМАФИЯ: ОТ ДИСКРЕДИТАЦИИ ОППОНЕНТОВ ДО ГЛОБАЛЬНОЙ МОНОПОЛИИ” (http://borisosadin.ru/favorite.htm).

“Теперь нередко говорят, что советская наука взорвалась вместе с 4-м блоком Чернобыльской АЭС. Однако больше оснований полагать, что она неслышно скончалась в середине 70-х гг. прошлого столетия.

В 1975 г. пост президента АН СССР оставил М.В.Келдыш – последний из трёх “великих К” (Курчатов-Королёв-Келдыш), что олицетворяют собой исторический феномен под названием “советская наука”… Келдыша на президентском посту сменил директор ИАЭ им. Курчатова 72-летний академик А.П.Александров, опытный организатор, но человек от фундаментальной науки достаточно далёкий. И тут же академики Е.П.Велихов и Б.Б.Кадомцев опубликовали в печатном органе ЦК КПСС статью, в которой и сейчас можно прочесть слова: “”Токамак-10” – последний шаг перед испытательным (демонстрационным) реактором… Исследования по управляемому термоядерному синтезу вступают в новую фазу… Можно ожидать решения этой проблемы в течение ближайших пяти-шести лет… Тогда на конец этого века можно будет планировать начало создания термоядерной энергетики, определить её место и роль в энергетическом балансе СССР. В преддверии XXV съезда КПСС учёные института им. И.В. Курчатова будут трудиться с ещё большим творческим подъёмом…”.

В том же 1975-м в Политехническом музее как партийное задание был выставлен муляж “Токамака-10”. Рождённая Власовым и поддержанная Завойским натурфилософия плазмы была отброшена. На смену осмысленным плазменным экспериментам пришло тотальное токамакостроительство. А на смену отдельным и разным учёным – подчиняющийся жёсткой дисциплине корпоративный монстр, который мало что делал, но всё и всех контролировал. Указанные события и можно считать той точкой невозврата, после которой пустые обещания стали в советской науке заурядным явлением, породившим и массовую безответственность учёных, и Чернобыльскую катастрофу, и многое ещё что.

Когда Советского Союза не стало, наука на постсоветском пространстве провалилась в хаос. Но одновременно появилась надежда на её возрождение на иных, более цивилизованных, началах. Этого не произошло по двум причинам. Во-первых, постсоветской российской власти долгое время было не до науки. Во-вторых, в то время как “научный планктон” или уходил из науки, или пытался приспособиться к новым условиям бытия, “научные вожди” действовали. Уже во времёна Хрущёва соперничество советских и американских атомщиков более походило на негласное сотрудничество. В брежневские времена оно стало почти гласным. Пугая правительства своих стран мнимыми научно-техническими достижениями мнимых противников, те и другие обеспечивали привилегированное финансирование своих исследований и разработок. Исчезновение СССР грозило положить конец такому положению вещей. И бывшие “противники” стали союзниками по международным проектам и международным организациям, создаваемым под проекты.

Ну, а в начале XXI в. то и другое предстало пред далёкой от науки публикой уже в оформленном виде. Как заявил недавно академик Э.П.Кругляков, в разных странах мира построено около 100 токамаков. Казалось бы, Кругляков знает, что говорит (ведь именно он возглавляет Комиссию РАН по лженауке). Но, опровергая Круглякова, сайт www.iter.org указывает на более чем 200 таких установок. Впрочем, что 100, что 200 – ни один из построенных токамаков, независимо от технических параметров и места нахождения, не дал никому ни джоуля энергии, ни ватта мощности. В настоящее время так называемое международное термоядерное сообщество (МТС), став мировым плазменным монополистом, обещает человечеству термоядерный рай лишь после 2030 г. Тем самым 5-6-летнее обещание академиков Велихова и Кадомцева образца 1975 г. пролонгировано на полвека. Но как удаётся столь долго и столь успешно торговать дырками от бублика? А удаётся благодаря не лишённому наукообразия мифотворчеству.

Миф №1 – это скорое исчерпание углеводородов, после которого человечество ожидает энергетический коллапс. Сотворён он был достаточно давно, однако и нефтепроводы, и газопроводы продолжают строиться. Но когда-то углеводороды всё же закончатся? Разумеется, да. Но из этого вовсе не следует, что надо строить токамаки. Есть другие источники энергии и, прежде всего, Солнце – природный термоядерный реактор, щедрость которого безмерна.

Миф №2: пока наши недоброжелатели вспоминали о Власове и Ландау, Арцимовиче и Завойском и каких-то там истринских экспериментах, мы, МТС, трудясь в поте лица, прошли путь от десяти в минус одиннадцатой до десяти в первой степени мегаватт термоядерной мощности. И теперь　 “научных проблем здесь больше нет – только инженерные” (Е.П.Велихов). Психологически миф этот выстроен достаточно точно, и на непосвящённых производит впечатление. Но попробуем разобраться.

Отделить научные проблемы от инженерных не всегда просто. Однако совершенно очевидно, что, прежде чем говорить о решённости или нерешённости тех или иных проблем, их, как минимум, надо назвать. Может быть, МТС разобралось с функциями распределения электронов и ионов в токамаках? Или с самосогласованным электрическим полем? Или с турбулентным нагревом? Или с кинетикой пристеночного плазменного слоя и механизмом удержания плазмы? А регистрируемые нейтроны – они действительно термоядерные или ускорительно-ядерные?.. Число подобных (научных) вопросов можно множить и множить. Но плазменная наука пока слишком несовершенна, чтобы сколь-либо определённо отвечать на них – о чём свидетельствует и число построенных токамаков…

Но, может быть, токамакостроители рассчитали КПД будущей термоядерной электростанции и доказали её коммерческую целесообразность?.. И снова нет. Что же касается “успеха”, достигнутого на европейском токамаке JET (кратковременная регистрация 　в преддверии очередного Миллениума – вместо очередного съезда КПСС – 16 МВт мощности), то никаких проблем – ни научных, ни инженерных – он не разрешил. Нейтроны получал и Арцимович. Получал и Завойский. Токамак JET дал их больше? Так и объём плазмы был больше, и денег на сооружение JET ушло больше. Больше денег – больше нейтронов. Только и всего. Проблемы же как были, так и остались. Да и что с ними делать, с токамачными-то нейтронами?..

Миф №3: наши недоброжелатели – это научные отщепенцы, а нас, то есть МТС, поддерживает всё мировое сообщество.

В известной мере и пока это действительно так. Без поддержки бывших президентов СССР, США и Франции (Горбачёва, Рейгана и Ширака) проект ITER никогда бы не состоялся, а сотни физиков и инженеров разных стран никогда не получили бы работы и заработка (что и заставляет последних воздерживаться от высказываний по сути того, чем они заняты). Но ни руководители стран-участниц ITER, ни сотрудники недавно оформившейся Организации ITER – это ещё не мировое сообщество.

Как ни странно (на самом деле закономерно), первым к перезагрузке плазмодинамических представлений ещё в 70-х гг. прошлого столетия призвал нобелевский лауреат по физике плазмы шведский физик Альфвен. Именно он назвал разработанную им, а затем усвоенную многими, в том числе Арцимовичем, плазмодинамическую парадигму теорией “псевдоплазмы”, то есть не существующей в природе субстанции. Однако токамакостроители призыв Альфвена проигнорировали.

После развала СССР заговорили некоторые бывшие сотрудники ИАЭ. И один из них, доктор С.И.Яковленко, счёл необходимым выпустить препринт, в котором написал: “…предвижу резкую критику и разнообразные обвинения от тех, кто заинтересован в том, чтобы бесконечно долго искали чёрную кошку в тёмной комнате, не включая света… На чём основано мнение, что нет принципиальных препятствий к достижению технического успеха?.. Ошибкой, не имеющей моральных оправданий, было разделение учёных на “чистых” и “нечистых” по принципу верности токамачной идее. Это породило в частности явление, получившее в научном фольклоре название токамафия. Речь идёт о формировании довольно большого клана учёных разного уровня, объединённых стремлением продвинуть токамачное направление любой ценой, в первую очередь ценой подавления других исследований”. Подобные слова в 90-е гг. воспринимались многими российскими физиками как глоток свежего воздуха, но одновременно подталкивали “токамафию” к наднациональному объединению. Кое и состоялось.

В 2006 г., отвечая на вопрос о перспективах термояда, первый заместитель научного руководителя РФЯЦ-ВНИИЭФ академик РАН Ю.А.Трутнев сказал: “Я этой проблемой не занимаюсь и не верю в неё. Считаю, что все эти работы – это удовлетворение учёными своей любознательности за счёт государства. Исследования в области термояда сейчас продолжаются, но я не верю, что термояд станет источником энергии даже в несколько отдалённом будущем”. Тем самым и в РАН появились “недоброжелатели” МТС.　

Не молчат и зарубежные учёные. На сайте http://candobetter.org можно ознакомиться со статьей сотрудника ЦЕРН доктора М.Диттмара “Иллюзии синтеза – проект ITER и снабжение тритием”. Достаточно детально обсудив проблему, автор пришёл к следующим выводам: “В настоящее время во всех существенных областях имеющиеся достижения всё ещё на много порядков величины отстают от тех, что необходимы для создания прототипа термоядерного реактора. Не существует материалов или структур, способных работать в условиях экстремально высоких нейтронных потоков, ожидаемых в реалистичных условиях слияния дейтерия с тритием. Самоподдерживающийся бридинг (воспроизводство – Б.О.) трития, необходимый для обеспечения функционирования коммерческого термоядерного реактора, представляется невозможным. Налогоплательщики, политики и средства массовой информации должны осознать, что после 50 лет весьма дорогостоящих исследований, проводившихся в разных странах мира, накоплено вполне достаточно знаний, чтобы утверждать, что коммерческое производство энергии за счёт управляемого ядерного синтеза не станет реальным никогда”.

Тем временем на юге Франции дейтерий-тритиевый реактор, называемый ITER и представляющий собой то ли 101-ый, то ли 201-ый токамак, продолжает строиться. Чего от него ждать? 10 миллиардов евро will simply evaporate (просто испарятся).

У Организации ITER нет никаких оснований любить Интернет, но она вынуждена им пользоваться. Пока организация эта создавалась и добивалась финансирования, на сайте www.iter.org размещались материалы, призванные демонстрировать сверхкомпетентность членов МТС в области физики плазмы. Но пошли письма “недоброжелателей” – и такие материалы исчезли. В настоящее время сайт представляет собой вполне заурядную рекламу строящегося объекта туристического показа под названием ITER-токамак. Полная масса 23 тыс. тонн (три башни Эйфеля), длина проводов сверхпроводящих катушек 150 тыс. км (более 3-х окружностей Земли), объём вакуумной камеры 1400 кубометров, объём гелиевого криостата 8500 кубометров, предварительная стоимость проекта 10 миллиардов евро. О плазме, которой пока нет, сказано, что её объём будет равен 850 кубометрам, а температура – 150 млн. градусов (около 15 кэВ, в десять раз больше, чем в центре Солнца). Пять лет назад на том же сайте и для того же ITER температура указывалась в полтора раза меньшая. Но реклама всё терпит, к тому же, помимо традиционного для токамаков токового нагрева плазмы, в ITER предусмотрены нагрев инжекцией нейтрального пучка и нагрев электромагнитными волнами (то есть по Завойскому).

Ну, а заветная цель проекта: вложить в плазму 50 МВт, а получить 500 МВт (Q = 10). И пропагандисты МТС немало постарались, чтобы убедить непосвящённых, что это будет реальная, то есть полезная мощность. Ознакомившись с перечисленными характеристиками, потрясённый посетитель сайта может с него и уйти, чтобы следом отправиться во Францию для ознакомления с новоявленным чудом наяву. Но в сознании некоторых возникает вопрос: сколько же этот супертокамак будет потреблять электроэнергии сам? Открыв страницу сайта под названием “Power Supply”, некоторые обнаруживают, что интересующая их величина составляет от 110 МВт до 620 МВт, вторая мощность относится к пиковым периодам продолжительностью 30 секунд, в течение которых будет существовать плазма и производиться термоядерная энергия. Но как же так? – начинают прозревать некоторые, – обещали Q = 10, а тут и единицы не набирается! А это как считать, дорогие некоторые. Затраты, например, на вакуумные насосы и криогенную систему можно включать в Q, а можно и не включать.

Ну, да Бог с ним, с этим Q, прощают МТС некоторые – зато три Эйфелевых башни и аж три окружности Земли! Но тут в их сознании возникает другой вопрос: ну, а 500 МВт –　 термоядерных – они-то куда пойдут? Какому-такому самому первому потребителю энергии управляемого термоядерного – долгожданной мечты человечества? И некоторые начинают метаться по сайту в поисках имени этого потребителя. И мечутся до тех пор, пока на странице “Cooling Water” не находят слова: “Чтобы сбросить тепло, вырабатываемое в процессе действия токамака, ITER будет оборудован системой водяного охлаждения. Поскольку ITER представляет собой исследовательский комплекс, а не электростанцию, большая часть охлаждающей воды will simply evaporate в охлаждающих башнях”. Ждать тем самым нечего, поскольку ITER – это реактор с нулевым КПД.

Всяк делает лишь то, что умеет: физики занимаются физикой, энергетики – производством энергии, а токамакостроители – сочинением наукообразных мифов и сбросом посредством токамаков не ими произведённой энергии в окружающую среду. Но, как сказал один небезызвестный президент, ещё никому не удавалось одурачить всех и на всё время”.

Входящие в число руководителей РАН академики Некипелов и Фортов являются также членами научно-координационной организации при Президиуме Российской академии наук, носящей название комиссии РАН по борьбе с лженаукой и фальсификацией научных исследований, которую возглавляет академик Кругляков. В числе постоянно и активно сотрудничающих с комиссией находится академик Захаров. Почему же столь выборочен, односторонен и предвзят выбор ими объектов для критики, явно осуществляемый с позиций указанной комиссии и объявленных ею целей и задач?

Вывод напрашивается один: подлинная цель работы комиссии РАН по лженауке и сотрудничающих с нею академиков состоит в том, чтобы, “выдавая чёрное за белое, а белое за чёрное”, отвлекая этим внимание научной общественности и руководства страны, “замести следы” совершаемого руководством Российской академии наук тяжкого государственного преступления!

Лагранжев формализм – историческое прошлое науки

Автор признателен безымянному оппоненту за возможность на его примере показать неадекватность лагранжева формализма для рассматриваемого класса задач.

Рассмотрим методы и средства, с помощью которых официальная наука “давит в зародыше” реальную альтернативу атомной и ядерной энергетике, каковой призвана стать, наряду с уже известными (солнечной, ветровой, приливной), также гравитационная энергетика вместе с (методологически и инструментально) связанными с нею системами безопорного движения, ныне совместно относимыми академической наукой к принципиально нереализуемым perpetuum mobile.

Ниже мы воспользуемся материалами обсуждения на Интернет-форуме статьи автора настоящих заметок “Кризис теоретической физики: признаки, причины, виновники (частный взгляд со стороны на академическую и вузовскую науку)” (http://bolshoyforum.org/wiki/index.php/).

Сразу приведём вывод оппонента, представляющего позицию официальной науки:

“…Приходим к подтверждению общеизвестного факта: работа, совершаемая силой тяжести за любой интервал времени, равна взятому с обратным знаком изменению потенциальной энергии системы в поле силы тяжести, и никакая энергия сверх этой из гравитационного поля извлечена быть не может. В данном случае во всех решениях потенциальная энергия в поле силы тяжести не зависит от времени, поэтому суммарная работа, совершаемая силой тяжести, равна нулю: правильно вычисленная положительная работа по раскачке колебаний компенсируется упущенной в статье Петрова работой по торможению вращения… Не боясь прослыть ретроградом, заявлю: не бывает гравитационных двигателей! Бывают самоуверенные и безграмотные люди, которые не умеют решать и даже правильно выводить уравнения движения для простейших механических задач”.

А теперь посмотрим, как оппонент к этому выводу приходит. Первую же фразу оппонента, дающего собственный расчёт предложенной автором принципиальной схемы гравитационного двигателя с неизменным потенциалом рабочей массы, мы вынуждены подправить. Оппонент представляет техническое решение автора в таком виде:

“Маховик в виде плоского круглого диска массы M и радиусом R, закреплённый на горизонтальной оси, раскручивается до некоторой "резонансной" частоты и затем переводится в свободное вращение”.

Уточняем: не в свободное, а в жёстко контролируемое (и, по необходимости, регулируемое) стабильное вращение на резонансной частоте ω (других частот, кроме кратных ω, у нас не будет, поэтому индекс 0 при ω в выкладках оппонента, для упрощения записи, будем опускать).

Цитируем оппонента:

“На диске на двух взаимно перпендикулярных направляющих, проходящих через центр диска, могут двигаться два тела, каждое массой m, закреплённых на пружинах жёсткости k. По смыслу задачи, после раскрутки маховика до резонансной частоты, тела начинают движение из центра диска и начинается "резонансная" раскачка колебаний за счёт действия силы тяжести, ускорение которой равно g. Обозначая координату первого из тел вдоль его направляющей с выбором нуля в центре как x, аналогично для второго тела вводим координату y и, наконец, обозначаем буквой φ угол между осью, по которой движется тело x, с горизонтальным направлением. В начальный момент времени считаем заданными нулевые значения для x, y и начальное "резонансное значение" для частоты вращения:

dφ/dt=ω, t=0.

Задача полностью поставлена. Лагранжиан системы, очевидно, имеет вид:

L=[(dφ/dt)²/2][MR²/2+m(x²+y²)]+(m/2)[(dx/dt)²+(dy/dt)²]–(k/2)(x²+y²)–

–mg[xsin(φ)+ycos(φ)]”.

Итак, оппонент применяет тот подход к решению динамической задачи, которому учит студентов высшая школа. Согласно этому подходу, ещё не решая задачи, можно представить все компоненты энергетического баланса системы, на основании которого затем составляется уравнение движения и, при необходимости, решается (а, возможно, и не решается, если достаточно лишь общего анализа энергетики движения).

Заметим: перед нами предстаёт “живая история науки”, своеобразная музейная экспозиция конца XVIII – начала XIX веков. Даже само представление функции Лагранжа в виде разности кинетической и потенциальной энергий системы – дань традиции или “знак уважения” к первой “классической” вариационной задаче о брахистохроне.

Напомним, что в “задаче о наискорейшем спуске” потенциальная энергия тела (на единицу массы) равняется g(d–h), где g – ускорение свободного падения, d – разность высот (или диаметр производящего круга), h – текущее снижение высоты движущейся точки. В этом случае кинетическая энергия тела (на единицу массы) равняется gh, а разность величин потенциальной и кинетической энергия оказывается пропорциональной косинусу угла поворота производящего круга: cosφ=1–2h/d, – что даёт решение задачи.

В других вариационных задачах такого замечательного результата не получается: в одном случае для решения задачи достаточно знания величины кинетической энергии, в другом – потенциальной энергии, в третьем – их суммы. В общем случае оказывается необходимым оперировать и кинетической, и потенциальной энергией, а их сведение к одной величине: к разности (функция Лагранжа) или к сумме (функция Гамильтона), – принципиального значения не имеет, поскольку оба формализма (лагранжев и гамильтонов) считаются эквивалентными.

Однако приведённые выше рассуждения корректны лишь в пределах вариационных задач на поиск экстремума. Заметим, что в функции Лагранжа присутствуют только два вида энергии: кинетическая, пропорциональная квадрату скорости, и потенциальная, пропорциональная координате или квадрату координаты. Других видов энергии метод Лагранжа не признаёт. Так, за рамками этого метода (и как бы за пределами механики!?) остаётся учёт диссипативных потерь (см., например, “Механику” Ландау-Лифшица, с. 100).

Отказ от рассмотрения диссипативных потерь в рамках механики оказывается ещё не худшим “выходом из положения”. С искусственным включением в метод Лагранжа учёта внешних сил обстоит дело хуже. В лагранжевом формализме осуществляется “пересчёт” конечного эффекта внешнего воздействия в некую “дополнительную потенциальную энергию системы”. Но можно ли корректно произвести такой “пересчёт”, ещё не имея решения задачи, т.е. не осуществляя интегрирования внешних сил по пути движения системы? Очевидно, нельзя. Значит, претензии метода Лагранжа на возможность решения динамических задач “в обратном порядке” (т.е. не на основе составления силового баланса с последующим вычислением энергетических характеристик, а, наоборот, получением силового баланса путём частного дифференцирования компонентов энергетического баланса) несостоятельны. Отсюда, в общем случае, и неадекватность этого метода. Покажем, в чём это выражается, на примере приведённой оппонентом функции Лагранжа.

Исходя из того, что внешняя сила, действующая вдоль оси координат х, равняется –mgsin(φ), а вдоль оси координат y равняется –mgcos(φ), оппонент “пересчитывает” внешнее воздействие в “дополнительную потенциальную энергию системы” (терминология Ландау-Лифшица), равную mg[xsin(φ)+ycos(φ)]. Здесь, вместо интегрирования внешней силы по координате (для определения величины энергии, поступающей в систему за счёт работы внешней силы), внешняя сила умножается на координату. Но отсюда следует явно ошибочный вывод о том, что, при линейном во времени росте амплитуды колебаний, накапливаемая в системе энергия будет также расти линейно во времени (хотя хорошо известно, что энергия при резонансе растёт квадратично во времени).

Оппонент поступает в точности, как Ландау-Лифшиц при рассмотрении вынужденных колебаний на странице 82 своей “Механики”, где поступающая в систему энергия, за счёт работы внешней силы, также получается умножением внешней силы F(t) на координату х. Правда, уже на следующей странице (сс. 83-84) авторы “Механики” эту ошибку исправляют. Они интегрируют силу F(t) по координате х и получают правильный вывод:

“Таким образом, в случае резонанса амплитуда колебаний растёт линейно во времени (до тех пор, пока колебания не перестанут быть малыми и вся излагаемая теория перестанет быть применимой)… Энергия системы, совершающей вынужденные колебания, разумеется, не сохраняется: система приобретает энергию за счёт источника внешней силы… Передача энергии … определяется квадратом модуля компоненты Фурье силы F(t) с частотой, равной собственной частоте системы”.

Но оппонент аналогичной поправки в свои выкладки не вносит, а “исправляет” ошибку тем, что путём частного дифференцирования функции Лагранжа получает правильные уравнения движения в виде силового баланса (тем не менее, в энергетическом балансе ошибка сохраняется, что должно проявиться позднее). Читаем далее:

“Уравнения движения получаем методом Лагранжа. Помимо уравнений для x, y дадим также выражение для их комплексной линейной комбинации, z=x+iy:

md²x/dt²+[k–m(dφ/dt)²]x= –mg sin(φ),

md²y/dt²+[k–m(dφ/dt)²]y= –mg cos(φ),

md²z/dt²+[k–m(dφ/dt)²]z= –img exp(–iφ). (1)”.

Кажется, что путь к решению задачи открыт. Чтобы в условиях действия центробежных сил (путём их компенсации) обеспечить режим резонанса, необходимо удвоить жёсткость возвратного механизма, и тогда уравнения (1) будут иметь обычный для такого режима вид:

md²x/dt²+mω²x= –mg sin(ωt),

md²y/dt²+mω²y= –mg cos(ωt),

md²z/dt²+mω²z= –img exp(–iωt).

Решение этих уравнений показывает линейный во времени рост амплитуды колебаний (и, естественно, квадратичный рост энергии системы):

x=(gt/2ω)cos(ωt),

y= –(gt/2ω)sin(ωt),

z=(gt/2ω)exp(–iωt).

А далее должна была бы следовать оценка того, достаточно ли накапливаемой в системе энергии для того, обеспечить стабильное вращение системы с угловой частотой ω. Но оппонент приступает к рассмотрению режима свободного вращения системы (без стабилизации угловой частоты), что, естественно, ведёт к нарушению условий резонанса и к затуханию колебаний. Но ведь это уже совсем иная задача. Читаем:

“Вместо же уравнения для φ, определяющего систематическое замедление вращения по мере раскачки колебаний

d/dt{dφ/dt[MR²/2+m(x²+y²)]}= –mg[xcos(φ)–ysin(φ)]= –imgR[exp(–iφ)], (2)

можно воспользоваться сохранением энергии для системы с Лагранжианом, не зависящим явно от времени:

[(dφ/dt)²/2][MR²/2+m(x²+y²)]=(ω²/2) MR²/2–(m/2)[(dx/dt)²+(dy/dt)²]–

–(k/2)(x²+y²)–mg[xsin(φ)+ycos(φ)].

Или, через комплексное z (звёздочка обозначает комплексное сопряжение, введено также обычное обозначение для действительной части комплексного числа):

(dφ/dt)²={ω²MR²/2–m(dz/dt)(dz/dt)*–kzz*–mgR[–izexp(iφ)]}/[(MR²/2)+mzz*].

(3)”.

Итак, введением постулата о сохранении энергии открытая система подменяется замкнутой, что предопределяет негативный итог анализа. Читаем далее:

“Решения в отсутствие диссипации.

Нетрудно найти решение полученных уравнений в виде вращения с постоянной частотой

ω=dφ/dt.

Имеем: из (1):

z = [–ig exp(–iφ)]/(k/m–2ω²).

Правая часть (2) при этом обращается в ноль, что согласуется с предположением о постоянстве частоты. На первый взгляд может показаться, что выбор "резонансной частоты" ω=√k/(2m) в качестве начальной частоты вращения (поразительно, но в критикуемой работе выражение для резонансной частоты вообще не получено) допускает неограниченную (точнее ограниченную только диссипативными процессами) раскачку колебаний. Однако это грубейшая ошибка, возникшая из-за забвения о законе сохранения энергии или, что то же самое, о соотношении (3) для частоты вращения. В действительности при таком выборе для начальной частоты вращения после некоторого роста колебания частота вращения в соответствии с (3) существенно понизится, после чего система выйдет из резонанса и рост колебаний прекратится (это хорошо известный и описанный в учебниках эффект нелинейного самоограничения резонанса). Нетрудно показать, что при любом выборе начальной частоты вращения, установившаяся после роста колебаний частота вращения будет либо несколько ниже, либо несколько выше резонансной, но никогда не попадет точно в резонанс”.

Конечно, “установившаяся после роста колебаний частота вращения” относится уже к другому режиму резонанса, с диссипативными потерями и полезной нагрузкой, так что и величина резонансной частоты будет иная. А резонансной эта частота признаётся потому, что она отвечает уравнениям движения с установившейся амплитудой вынужденных (резонансных) колебаний системы.

Приведём заключительную часть выполненного оппонентом анализа, правда, уже не имеющую к решаемой нами задаче прямого отношения:

“Решения при наличии диссипации.

Эта часть работы Петрова совершенно абсурдна и возникла как следствие грубого игнорирования уравнения движения (2). При добавлении в уравнение (1) пропорциональной скорости силы трения –mνdz/dt это уравнение принимает вид:

md²z/dt²+mνdz/dt+[k–m(dφ/dt)²z = –img exp(–iφ). (4)

Сразу отмечу что работа, совершаемая силами трения за единицу времени, отрицательна и равна

–W= – mν(dz/dt)(dz/dt)*.

Уже хотя бы из этих соображений представляется очевидным, что поддержание постоянной (особенно резонансной) частоты вращения в системе с потерями невозможно без постоянно затрачиваемой внешней мощности. Действительно, решение уравнения (4) для постоянной частоты вращения получить нетрудно:

z = [–ig exp(–iωt)]/(k/m–2ω²–iων).

Однако правая часть (2) при этом отнюдь не обращается в ноль! Для поддержания частоты вращения постоянной в правую часть (2) необходимо добавить развиваемый некоторым внешним двигателем постоянно действующий момент сил, равный, очевидно,

T = mgR[z exp(iφ)].

Вычисление действительной части даёт:

T = (mg²ων)/[(k/m–2ω²)²+ ω²ν²] = mνωzz* = W/ω.

Мощность, которую должен развивать внешний двигатель для поддержания такого момента сил, равна ωT = W! Таким образом, мощность диссипации энергии колебаний (что и является полезной мощностью данного "гравитационного двигателя") всецело заимствуется из внешнего двигателя – а если последний отсутствует, поддержание стационарной резонансной частоты вращения и раскачка колебаний до диссипативного предела не представляются возможными.

О невозможности извлечения энергии из гравитационного поля.

Домножим первое из уравнений (1) на dx/dt. Правая часть уравнения – это работа, совершаемая за единицу времени силой тяжести над частицей x. Аналогично, домножим второе из уравнений (1) на dy/dt. Правая часть уравнения – это работа, совершаемая за единицу времени силой тяжести над частицей y. Наконец, домножим уравнение (2) на dφ/dt. Среднее из выражений это будет работа, совершаемая моментом силы тяжести над вращающейся системой. Суммируя эти три члена, получаем полную работу, совершаемую гравитационной силой за единицу времени, которую преобразуем следующим образом:

–(dx/dt)mg sin(φ)–(dy/dt)mg cos(φ)–(dφ/dt)mg[x cos(φ)–y sin(φ)] = –dU/dt,

U=mg [xsin(φ)+ycos(φ)],

где введена потенциальная энергия масс x, y в гравитационном поле…”.

Если бы оппонент придерживался условий задачи, решаемой автором, то его уравнение (4) выглядело бы так:

md²z/dt²+mνdz/dt+ω²z = –img exp(–iωt).

Это уравнение имеет следующее решение:

z = (g/νω) exp(–iωt).

Комплексная форма записи в данном случае имеет смысл формального объединения двух колебательных процессов в один исключительно для удобства аналитика. Поэтому применять правило умножения сопряжённых комплексных чисел при вычислении работы сил трения и энергетических затрат на полезную нагрузку здесь не нужно. Раздельно вычисляя эти энергетические затраты для каждого из двух процессов, получаем суммарную мощность, развиваемую системой:

W=mg²/ν.

Учитывая, что максимальное значение полезной мощности системы достигается при равенстве внутренней (затратной) и внешней (полезной) нагрузок, а также снижая ещё вдвое полезную мощность с учётом “балластных” свойств маховика, выполняющего функцию стабилизации вращения, мы в качестве теоретического предела полезной мощности принимаем четвёртую часть этой величины.

Однако к вопросу об энергетических затратах на поддержание стабильной частоты вращения системы эта величина никакого отношения не имеет. Оппонент рассматривает (вполне обоснованно) колебательные процессы во вращающейся системе координат, поэтому переменные величины здесь одномерные. Но далее, продолжая его исследование, надо было бы вводить в рассмотрение кориолисовы ускорения и, исходя из этого, предлагать возможные способы их нейтрализации. Однако мы предпочитаем вопросы стабилизации вращения рассматривать в неподвижной системе координат, что оппонент во внимание уже не принимает.

Заметим, что, возвращаясь к энергетическим характеристикам системы, оппонент невольно подтверждает факт совершённой ранее ошибки, о которой уже шла речь выше и которая относится к неисправимым порокам лагранжева метода, вынужденно определяющего работу, совершаемую гравитационной силой, не интегрированием силы по пути реального движения системы (найденному из решения уравнения движения), а умножением внешней силы на (неизвестное!) перемещение системы.

Главная же беда в том, что лагранжев метод решения динамических задач, основанный на узко понимаемом законе сохранения энергии и заведомо не адекватный открытым динамическим системам, уже долгое время остаётся неотъемлемой, ограждаемой от малейшей критики и монопольно безальтернативной методологической основой теоретической физики.

Двигатель с неизменным гравитационным потенциалом

Логически продолжая вышеизложенное, заметим, что мы синтезируем систему из двух точечных (рабочих) масс, способных под внешним гравитационным воздействием совершать гармонические колебания в перпендикулярных направлениях на плоскости вблизи начала координат. Для того, чтобы гравитационное воздействие стало переменным по направлению, система приводится во вращение с угловой скоростью w. Соответственно, жёсткость возвращающего механизма подбирается так, чтобы (с поправкой на центробежные силы) частота собственных колебаний масс равнялась w и работа системы приобрела резонансный характер.

Для уяснения основного принципа и конечного эффекта работы системы достаточно было бы рассмотреть лишь установившийся режим. Но поскольку оппонент начинал свой анализ с нулевого уровня колебаний в системе, мы также кратко опишем его.

Сначала рассмотрим синтезируемую нами систему во вращающейся (синхронно с реальным вращением) системе координат. В этой системе координат сила притяжения совершает обратное вращение с той же угловой скоростью w. Обозначим координату массы, колеблющейся вдоль оси абсцисс, через α, а вдоль оси ординат – через β. Законы колебаний масс на начальной стадии резонансного процесса (при пренебрежимо малых диссипативных потерях и отключённой полезной нагрузке) описываются следующими уравнениями (приведёнными к единичной массе; здесь g – ускорение свободного падения на поверхности Земли):

d²α/dt²+w²α= –g sin(wt),

d²β/dt²+w²β= –g cos(wt).

Соответственно, решениями этих уравнений являются следующие функции времени:

α(t)= (gt/2w) cos(wt),

β(t)= –(gt/2w) sin(wt).

Возникающие при этом побочные эффекты в виде кориолисовых ускорений, как и способы их нейтрализации, мы рассматриваем в абсолютной (не вращающейся) системе координат. В невращающейся системе координат движение масс будет уже не одномерным, а плоскостным, что заставляет нас рассматривать это движение на комплексной плоскости в виде функций x(t) и y(t) с изменяющимися во времени модулями (найденными нами выше функциями α и β) с фазовыми множителями вращения exp(iwt):

x(t)=(gt/2w)cos(wt)exp(iwt),

y(t)= –i(gt/2w)sin(wtexp(iwt)).

Дифференцируя эти функции по времени, находим векторы скоростей и ускорений:

dx/dt=(g/2w)cos(wt)exp(iwt)–(gt/2)sin(wt)exp(iwt))+i(gt/2)cos(wt)exp(iwt),

d²x/dt²= –gsin(wt)exp(iwt)+gwtcos(wt)exp(iwt)+

+igcos(wt)exp(iwt)–igwtsin(wt)exp(iwt);

dy/dt= –i(g/2w)sin(wt)exp(iwt)+i(gt/2)cos(wt)exp(iwt))+(gt/2)sin(wt)exp(iwt),

d²y/dt²= –igcos(wt)exp(iwt)+igwtsin(wt)exp(iwt)+

+gsin(wt)exp(iwt)+gwtcos(wt)exp(iwt).

Оценим побочные эффекты торможения-ускорения в тангенциальных направлениях за счёт изменения радиусов вращения рабочих масс. Для массы, движение которой описывается функцией x(t), тангенциальное направление будет соответствовать мнимой единице перед модулем функций, описывающих её скорость и ускорение. Для другой массы тангенциальное направление будет соответствовать действительной величине модуля. Вычисляя скалярные произведения этих составляющих и умножая на величину массы m, получаем затраты энергии, необходимые для поддержания стабильной частоты вращения w (соответственно, для одной и другой массы):

Пx=m[gcos(wt)–gwtsin(wt)]·(gt/2)cos(wt)=mg²t/4+(mg²t/4)cos(2wt)–

–(mg²wt²/4)sin(2wt).

Пy=m[gsin(wt)+gwtcos(wt)]·(gt/2)sin(wt)=mg²t/4–(mg²t/4)cos(2wt)+

+(mg²wt²/4)sin(2wt).

Если побочные явления на удвоенной частоте вращения взаимно компенсируют друг друга, то наличие постоянной составляющей указывает на то, что выход системы на основной режим работы потребует определённых дополнительных затрат мощности (принципиального значения не имеющих, поскольку речь всё-таки идёт о переходном режиме).

А теперь рассмотрим установившийся режим работы системы (с диссипативными потерями и полезной нагрузкой, что совместно учитывается в коэффициенте b затухания свободных колебаний в системе).

Рассмотрим движение двух точечных масс на комплексной плоскости вблизи начала координат О такое, что одна из масс совершает гармонические колебания единичной амплитуды с угловой частотой w вдоль действительной оси, а другая – вдоль мнимой оси i. Физическое тело (в техническом исполнении – маховик), с которым жёстко связана комплексная плоскость (она же – плоскость вращения) и к которому динамически подвешены точечные массы, вращается с угловой частотой w вокруг начала координат (на рис.1 – против часовой стрелки). Тогда характеристики абсолютного движения (координаты, скорости и ускорения) каждой из масс будут описываться функциями времени следующего вида:

x = cos(wt) exp(iwt),

dx/dt = –w sin(wt) exp(iwt) + iw cos(wt) exp(iwt),

d²x/dt² = –2w² cos(wt) exp(iwt) – i2w² sin(wt) exp(iwt),

y = –i sin(wt) exp(iwt),

dy/dt = – i w cos(wt) exp(iwt) + w sin(wt) exp(iwt),

d²y/dt² = i 2w² sin(wt) exp(iwt) + 2w² cos(wt) exp(iwt).

Каковы характерные особенности такого совместного движения масс? Во-первых, сумма их координат (x и y) неизменно равна единице:

x+y= (coswt – i sinwt) exp(iwt) = exp(–iwt) exp(iwt) =1

а это означает, что общий центр двух масс постоянно находится на действительной оси координат в точке ½.

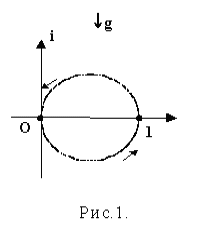
Во-вторых, суммарный момент инерции масс относительно начала координат (сумма квадратов модулей вектор-функций) остаётся величиной постоянной:

|x|²+|y|²= cos²wt + sin²wt = 1.

В-третьих, моменты импульсов масс относительно начала координат (произведения модулей вектор-функций на модули тангенциальных составляющих скоростей) возрастают в нижней комплексной полуплоскости от нулевого значения до максимального и убывают в верхней полуплоскости от максимального до нулевого (в момент прохождения положения равновесия в начале координат), при этом их сумма остаётся величиной постоянной:

|cos(wt)exp(iwt)|•|iwcos(wt)exp(iwt)|+|isin(wt)exp(iwt)|•|wsin(wt)exp(iwt)|=w.

В-четвёртых, ускорения масс в любой момент времени равны по модулю и направлены встречно, так что их сумма постоянно равна нулю.

Всё перечисленное теоретически исключает влияние колебательных движений масс на величину угловой скорости их совместного вращения. Тем не менее, при технической реализации системы, в качестве дополнительной меры по обеспечению стабильности вращения, можно применить дублирование таких колебательных пар с фазовыми (пространственными) сдвигами на 45°, 30° и т.д.

В неподвижной (“абсолютной”) системе координат очевидна асимметрия данного движения в виде горизонтального, вдоль действительной оси, смещения центра (рабочих – вращающихся и колеблющихся) масс. Однако остаётся неясным основной, интересующий нас, вопрос о характере реакции данной системы на внешнее гравитационное воздействие (направленное по вертикали вниз, к центру Земли, если система находится на её поверхности). Для получения ответа на этот вопрос представим движение масс в относительной, а, именно, жёстко связанной с вращающимся телом (маховиком), системе координат.

В случае пассивной массы роль последней сводилась бы к трансляции гравитационного воздействия на неподвижную опору, реакция которой уравновешивала бы силу тяготения, предотвращая свободное падение массы. Но в нашем случае обе массы продолжают свои движения вдоль координатных осей (теперь принятых нами за неподвижные), а внешняя сила (в обратном вращении) изменяется по гармоническому закону со сдвигом для этих масс по фазе на 90° и по времени на четверть периода вращения.

Запишем уравнения движения для каждой из масс, полагая, что в коэффициент упругости возвращающей силы внесена поправка на центробежную силу, линейно возрастающую с удалением от начала координат (с этой поправкой собственная возвращающая сила “пружины” должна возрастать и убывать вдвое быстрее):

d²α/dt²+b dα/dt+w²α= –g sin(wt)

d²β/dt²+b dβ/dt+w²β= –ig cos(wt)

где b – удвоенный коэффициент затухания свободных колебаний в системе, [–gsin(wt)–igcos(wt)]= –igexp(–iwt) – ускорение свободного падения на поверхности Земли во вращающейся системе координат, с фазовым множителем обратного вращения, разложенным по осям координат.

Решая уравнения, получаем:

α=(g/bw)cos(wt),

β= –i(g/bw)sin(wt).

Как видим, постоянный по модулю суммарный вектор отклонения масс от положения равновесия совершает, вслед за вектором силы тяготения, обратное вращение, отставая от него по фазе (и положению в пространстве) на 90°:

α+β=(g/bw)cos(wt) – i(g/bw)sin(wt)=(g/bw)exp(–iwt).

Исключая множитель обратного вращения (т.е. возвращаясь в неподвижную систему координат), обнаруживаем, что с точностью до модуля найденное решение совпадает с движением, изображённым на рис.1. Но теперь, пользуясь уравнением движения, мы в состоянии до конца проанализировать и понять динамику системы.

Внешнее воздействие, направленное по вертикали вниз, (сила тяготения) уравновешивается создаваемой самóй системой отрицательной обратной связью по первой производной (так что сила тяжести вращающихся масс по вертикали вниз не передаётся), тогда как горизонтальное отклонение рабочей массы от положения равновесия, через ответную реакцию “возвратной пружины”, передаётся внешней опоре по горизонтали(!), где нет ограничений на возможные перемещения опоры вместе с центром масс по линии или поверхности равного гравитационного потенциала. Если же потери на трение и сопротивление среды окажутся достаточно малы, то горизонтальные перемещения опоры (к примеру, по кругу) смогут сопровождаться “стравливанием” излишка внутренней потенциальной энергии (“энергии сжатой пружины”) в “полезную нагрузку”.

В итоге, проблема создания гравитационного perpetuum mobile оказывается сугубо технической или технологической: как только внутренние потери динамической системы снизятся до уровня, отвечающего соотношению b“1, так станет целесообразным практическое освоение неисчерпаемого, вездесущего и экологически безупречного источника гравитационной энергии.

Умножая уравнение баланса сил на скорость движения системы и учитывая, что максимальное значение полезной мощности Рmax достигается при равенстве внутренней (затратной) и внешней (полезной) нагрузок, а также снизив ещё вдвое полезную мощность с учётом “балластных” свойств маховика, выполняющего функцию стабилизации вращения, получаем теоретический предел полезной мощности гравитационно-резонансных двигателей данного типа для работы в наземных условиях при величине суммарной рабочей массы m:

Р max = mg²/4b.

А теперь проверим, не “съедят” ли побочные эффекты всю поступающую в систему энергию. В невращающейся системе координат нам не придётся иметь дело с кориолисовыми ускорениями. К тому же, мы уже заранее продифференцировали координаты двух половинок рабочих масс, так что теперь надо только вычислить скалярные произведения тангенциальных составляющих скоростей и ускорений, чтобы оценить затраты энергии на поддержание стабильной частоты вращения. Для отдельной массы m имеем:

П=(2mgw/b) sin(wt) · (g/b) cos(wt) = (mg²w/b²) sin(2wt).

Как видим, среднее значение мощности, развиваемой силами торможения-ускорения, за полпериода основного вращения системы равняется нулю. При наличии более, чем двух частей рабочей массы, а также другими мерами можно добиться достаточно стабильной частоты вращения, а значит, и устойчивой работы системы с полезным выходом энергии. Естественно, предлагаемое техническое решение не единственно возможное.

С помощью подобных гравитационно-резонансных “вечных двигателей” может решаться и “обратная задача” преобразования накопленной энергии в поступательное движение транспортных средств и летательных (включая космические) аппаратов. Достаточно простой эксперимент, подтверждающий реальную возможность такой системы, описывается в следующем параграфе.

Наглядный эксперимент, реализующий безопорное движение

На примере открытой гравитационной системы мы рассмотрим эксперимент, подтверждающий принципиальную возможность как безопорного движения (до сих пор не признаваемого официальной наукой), так и гравитационной энергетики (пока, к сожалению, не признаваемой и большинством учёных).

Предлагаемый эксперимент доступен для воспроизведения на простейшей технической базе, а сопровождающие его расчёты, хотя и носят прикидочный характер, тем не менее дают возможность придти ко вполне определённым выводам.

Экспериментальная установка монтируется на стандартном двухколёсном велосипеде, который закрепляется на тележке так, чтобы ведущее заднее колесо имело возможность свободно вращаться, получая подкрутку от педалей. На спицах заднего колеса, с помощью пружин заданной жёсткости, располагаются грузы, имеющие возможность колебаться, в определённых пределах, вдоль спиц.

Назначим, с некоторой долей условности, конкретные значения характеристик создаваемой вращательно-колебательной динамической системы. Исходя из длины внешней окружности колеса 1,5 метра и скорости велосипеда при езде по шоссе 40 км/час, выберем приемлемую величину угловой скорости вращения колеса: ω=(40000·2π)/(3600·1,5)=46,5 радиан/сек.

 

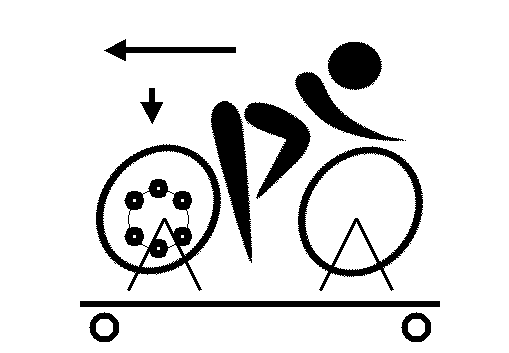
Рис. 2.

Пусть масса каждого единичного груза, размещаемого на спице колеса, равняется 0,1 кг. При общем количестве спиц 36 общая масса всех колеблющихся грузов составит 3,6 кг. Длину спицы (от втулки, имеющей радиус 2,5 см, до внешнего обода) примем равной 25 см. Из этой длины лишь последние 15 см будут пригодны (в силу конструктивных особенностей велосипедного колеса) для размещения дополнительного (колеблющегося) груза. Таким образом, точку равновесия груза на спице оказывается на расстоянии 20 см от оси вращения колеса (и в 7,5 см от внутренней стороны обода).

В точке равновесия центробежная сила составит mω²r=0,1·46,5²·0,2=43,25 ньютона. Этой же величине (с обратным знаком) должна быть в данной точке равна и сила компенсирующей пружины. В произвольной точке на спице (в рабочем интервале с 12,5 до 27,5 см от оси вращения) возвратная пружина не только должна компенсировать величину центробежной силы, но и, сверх того (для обеспечения гармонического вида колебаний), должна быть пропорциональна величине отклонения от точки равновесия, т.е. с удалением от точки равновесия в ту или другую сторону возвращающая сила должна возрастать или убывать вдвое быстрее и, таким образом, суммарная жёсткость возвратной пружины составит величину 2mω²=432,5 Н/м. С изменением расстояния r от оси вращения возвращающая сила будет изменяться по закону F=43,25+432,5·(r–0,2) ньютона.

В чём будет состоять задача велосипедиста-испытателя? Его задачей будет раскрутить колесо до отвечающей условиям резонанса угловой частоты ω, которой соответствует шоссейная скорости 40 км/час (эту величину можно контролировать по спидометру, закреплённому на раме велосипеда и отслеживающему вращение колеса), а затем поддерживать неизменным установившийся режим вращения.

Проанализируем режим резонанса на комплексной плоскости, сначала во вращающейся вместе с колесом системе координат, а затем рассмотрим его же в неподвижной (относительно внешнего наблюдателя) системе координат.

Пусть действительная ось координат проходит через диаметр колеса по горизонтали вправо (рис. 2), а мнимая ось – по вертикали вверх через диаметр, перпендикулярный указанному выше. Выберем из 36 грузов четыре наиболее характерных, которые можно было бы (с некоторым допущением) считать расположенными на осях координат, попарно разнесёнными от оси вращения колеса (и начала координат) в разные стороны соответственно на (переменные в динамике) расстояния от начала координат α, β, γ и δ.

В начальный момент времени, после раскрутки колеса, но в отсутствие силы притяжения (для этого случая можно рассмотреть гипотетическую возможность вращения колеса не в вертикальной, а в горизонтальной плоскости) все четыре груза находятся в точках равновесия, на одинаковых расстояниях от начала координат: |α|=|β|=|γ|=|δ|=0,2 метра. На комплексной плоскости точки равновесия грузов имеют координаты: α=0,2; β=–0,2i; γ=–0,2; δ=0,2i. Соответственно, центробежные силы, приведённые к единичной массе грузов (и компенсируемые возвратными пружинами), в этих точках равны: 0,2ω²; –0,2iω²; –0,2ω²; 0,2iω².

Проигнорируем, в первом приближении, побочные тангенциальные составляющие сил притяжения грузов (о них будет отдельный разговор, однако учтём, что, кроме взаимной компенсации этих составляющих, проходящих разные фазы вращения, имеется также общее регулирующее влияние со стороны велосипедиста, поддерживающего равномерный режим вращения) и рассмотрим (“полезное” для системы) влияние радиальных составляющих силы тяжести на указанные четыре груза.

Чтобы оценить порядок величин, характеризующих интересующий нас резонансный процесс, рассмотрим режим установившейся амплитуды колебаний, для чего зададим определённую величину коэффициента сопротивления b, учитывающего суммарные диссипативные потери и влияние полезной нагрузки (при наличии таковой).

Итак, имеем четыре дифференциальных уравнения движения грузов в радиальных направлениях, приведённых к единичной массе (g – ускорение свободного падения, t – время):

d²α/dt²+(b/m)dα/dt+ω²α=0,2ω²+(g/m) sin ωt,

d²β/dt²+(b/m)dβ/dt+ω²β= –0,2iω² –i(g/m) cos ωt,

d²γ/dt²+(b/m)dγ/dt+ω²γ= –0,2ω²+(g/m) sin ωt,

d²δ/dt²+(b/m)dδ/dt+ω²δ=0,2iω²–i(/m)g cos ωt.

В начальный момент времени t=0 полагаем вектор силы притяжения направленным вниз, т.е. навстречу мнимой оси координат. Заметим, что, в любой паре сдвинутых на 90º составляющих силы притяжения, суммарный вектор силы притяжения совершает вращение в положительном направлении (против часовой стрелки), т.е. в обратном направлении относительно направления вращения колеса: g sin ωt–ig cos ωt= –ig exp(iωt).

Решая дифференциальные уравнения при заданных выше начальных условиях, получаем:

α=0,2–(g/bω) cos ωt,

β= –0,2i –(ig/bω) sin ωt,

γ= –0,2–(g/bω) cos ωt,

δ=0,2i –(ig/bω) sin ωt.

Замечаем, что полусумма смещений

(½)(α+β+γ+δ) =–(g/bω)cos ωt–i(g/bω)sin ωt==–(g/bω)exp(iωt)

представляет собой вектор, вращающийся по часовой стрелке (т.е. в обратном направлении относительно направления вращения колеса) с отставанием от вектора силы тяжести на 90º.

Убирая фазовый множитель обратного вращения exp(iωt), т.е возвращаясь в неподвижную систему координат, замечаем, что смещение общего центра масс грузов происходит в гроизонтальном направлении с кажущимся опережением вектора силы тяжести на 90º по ходу вращения колеса (что соответствует аналогичному факту и выведенному из него мнемоническому правилу определения направлений отклонения вращающихся объектов под внешним воздействием: волчков, вращающихся пуль, артиллерийских снарядов и т.д.).

Соответственно величине коэффициента сопротивления b амплитуда колебаний (или величина бокового смещения) стабилизируется на значении mg/bω. Чем меньше этот коэффициент, тем выше амплитуда колебаний (или величина бокового смещения). Однако в нашем случае имеется жёсткое техническое ограничение (длина спицы колеса), которое заставляет вести расчёт в обратном порядке: зная предельно допустимую величину смещения (0,075 м), определяем величину коэффициента сопротивления b, при котором это смещение достигается: b=g/0,075ω=2,8 (1/сек).

При меньших значениях коэффициента b необходимы дополнительные меры по изъятию излишков энергии из системы. Наиболее простой и естественный способ: предоставление возможности тележке, на которой закреплён велоситед, двигаться в направлении создаваемой силой тяжести тяги (на рис.2 влево по горизонтали), тем самым преобразовывая потенциальную энергию сжатых пружин колебательной системы в кинетическую энергию. Можно сделать именно такой выход (полезной) избыточной энергии единственным в системе. Тогда коэффициент b будет минимальным, учитывающим только диссипативные потери.

Произведём расчёт действующих в системе сил и развиваемых ими мощностей при заданном режиме её работы. На входе системы действует суммарная сила гравитации, равная: 3,6 кг · 9,81 м/с²=35,3 ньютонa.

Однако, эта величина представляет собой модуль вращающегося вектора силы притяжения “рабочих масс” (или сумма амплитуд отдельных составляющих). Эффективное же значение этого вектора в 1,414 раза меньше. При максимальном горизонтальном сдвиге общего центра масс грузов 0,075 метра возникающая при этом сила тяги составит (здесь также вводим коэффициент 1,414):

3,6кг·46,5²(рад²/с²)·0,075м/1,414=412 ньютонов.

Развиваемая силой гравитации активная мощность в системе будет равна:

3,6 кг·9,81² (м/с²)²/1,41·2,8=87,5 ватт.

Эта мощность будет распределяться между мощностью, развиваемой на полезной нагрузке, и мощностью диссипативных потерь энергии (для случая, когда системе не предоставлена свобода горизонтального перемещения). Однако, за вычетом мощности, рассеиваемой в виде диссипативных потерь, вся остальная часть развиваемой системой мощности может целиком трансформироваться в кинетическую энергию поступательного движения системы.

Учёт побочных эффектов, проводимый в невращающейся системе координат, аналогичен описанному выше для гравитационного двигателя с неизменным потенциалом рабочей массы как по методике проведения, так и по конечному результату. Одним из эффективных дополнительных методов нейтрализации побочных вращающих моментов с удвоенной частотой вибраций (относительно частоты вращения колебательной системы) может явиться установка специальных “запирающих фильтров” для колебаний на удвоенной частоте.

Описанный эксперимент, в силу своей простоты и наглядности, может явиться необходимым завершающим звеном в цепи уже проведённых экспериментов с системами безопроного движения, начиная с инерциоидов Толчина и кончая “гравицапой”, запущенной в космос на экспериментальном спутнике “Юбилейный”, и положить конец спорам о реальности их существования и целесообразности дальнейшей разработки и совершенствования.

Литература

• Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учеб. пособ.: Для вузов. В 10 т. Т. I. Механика. – 5-е изд., стереот. – М.: Физматлит, 2001.
• Петров А.М. Заявка № 97111689/06 на изобретение “Способ получения и использования гравитационной энергии в форме движения рабочей машины, транспортного средства или летательного аппарата”, с приоритетом от 15 июля 1997 года (архив Роспатента).
• Петров А.М. Гравитационно-резонансные “вечные двигатели” в природе и технике: математическое описание, возможные технические решения для систем наземного и космического применения, расчёт эффективности. – М.: Компания Спутник+, 2001.
• Петров А.М. Гравитация: методологическая адекватность теории открывает доступ к новому виду энергии на практике. A.Pétrov. Gravitation: l’adéquation méthodologique de la théorie ouvre l’accès à la source énergétique nouvelle en pratique. – М.: Компания “Спутник+”, 2003.
• Петров А.М. Гравитация и кватернионный анализ. 2-е издание. – М.: Тип. “Наука”. 2005. – 48 с.
• Петров А.М. Открытое письмо учёным-математикам по поводу методологического кризиса теоретической физики. – Москва, Компания Спутник+, 2007.
• Петров А.М. АнтиЭйнштейн: Переворот в науке, произведённый г-ном Альбертом Эйнштейном. – М.: Компания Спутник+, 2008.
• Петров А.М. К проблеме аксиоматической адекватности описания движения в физическом пространстве. Методические заметки. – М.: Компания Спутник+, 2008.
• Петров А.М. К теории инерциоидов, гироскопов, вихрей и … perpetuum mobile. – М.: Компания Спутник+, 2009.
• Петров А.М. Реактивная динамика открытых систем (резонанс, вихреобразование, гироскопия, электромагнетизм). – М.: Издательство “Спутник +”, 2010. http://www.sciteclibrary.ru/rus/catalog/pages/10319.html

См. также статьи на Интернет-форумах

• Кризис теоретической физики: признаки, причины, виновники (частный взгляд со стороны на академическую и вузовскую науку) http://bolshoyforum.org/wiki/index.php/

• Дефекты математической культуры теоретической физики

http://www.sciteclibrary.ru/rus/catalog/pages/10890.html

• "Математическое безвременье" в отечественной науке http://bolshoyforum.org/wiki/index.php/
• Апология науки прошлого и лженауки будущего

http://www.forum.za-nauku.ru/index.php/topic,549.0.html

• Задача о вращающемся волчке: постановка, решение, приложения http://bolshoyforum.org/wiki/index.php/

• Ab ovo или Ab hoc et ab hac? (ответ на статью “Ab Ovo или "... а Лагранж – против"”) http://bolshoyforum.org/wiki/index.php/
• Практический смысл идейной борьбы в науке

http://bolshoyforum.org/wiki/index.php/

Ссылки

• http://www.utro.ru/articles/2011/05/20/975491.shtml
• http://newsland.ru/News/Detail/id/707062/
• http://www.trinitas.ru/rus/doc/0231/007a/02311016.htm
• http://borisosadin.ru/favorite.htm

　 

Дата публикации: 8 июня 2011
Источник: SciTecLibrary.ru