О ДОКАЗАТЕЛЬСТВЕ ПОСЛЕДНЕЙ ТЕОРЕМЫ ФЕРМА
![]()
© Побиск Г. Кузнецов
(Опубликовано в 1974 г)
Светлой памяти моего учителя Петра Сергеевича Новикова - посвящаю.
((П.Г. Кузнецов))
… Используя принцип полной индукции можно доказать СУЩЕСТВОВАНИЕ некоторого математического ВЫВОДА.
И наоборот,
используя принцип полной редукции, нетрудно доказать, что некоторое положение
НЕ СУЩЕСТВУЕТ.

Автор полагает, что принцип полной редукции есть ни что иное, как "метод бесконечного спуска", которым так гордился великий Ферма.
Принцип полной редукции, хотя и использовался в истории математики, является единственным принципом, пригодным для машинной математики (для доказательства теорем), являясь методом "бесконечного спуска"….
---------ХХХ----------
ПРИНЦИП ПОЛНОЙ РЕДУКЦИИ,
КАК "ДВОЙНИК"
ПРИНЦИПА ПОЛНОЙ ИНДУКЦИИ
Обнаружение "двойника" ЕДИНСТВЕННОМУ принципу математического доказательства вряд ли может пройти незамеченным среди математиков.
Само собою разумеется, что этот принцип ИСПОЛЬЗОВАЛСЯ и ИСПОЛЬЗУЕТСЯ, но остается внутри обширного математического мира только НЕ НАЗВАННЫМ. Нами предлагается назвать этот принцип - принципом ПОЛНОЙ РЕДУКЦИИ.
Более пятидесяти лет автор искал практическое решение некоторых проблем химии и других предметных областей, используя аппарат различных ветвей математики.
Однако существует практически бесконечное множество различных математических теорий, относительно которых никто не может сказать - годится или не годится именно этот "математический инструмент" для решения прикладных проблем некоторого типа.
Обсуждение этого круга
проблем с П.С. Новиковым вывело меня на совокупность проблем, носящих название
"алгоритмически неразрешимых".
Именно здесь и обнаружился общий руководящий принцип, который пока не имел имени. Фактически мы обращаемся к минимальному члену ряда, т.е. к тому члену, который играет роль "ЕДИНИЦЫ".
Поскольку существует бесконечное множество различных "единиц", то они могут служить источником парадоксов. Приведем простой пример группы "неразрешимых" проблем:
1 + 1= 2;
1 + 1 = 1;
1 + 1= 0.
Не имеет смысла доказывать, какая из этих трех формул является "истинной": они все верны для различных ветвей математики.
Используя принцип
полной индукции мы можем доказать СУЩЕСТВОВАНИЕ некоторого математического
ВЫВОДА. Наоборот, используя принцип полной редукции, мы можем доказать, что
некоторое положение НЕ СУЩЕСТВУЕТ.
Мы полагаем, что принцип полной редукции есть ни что иное, как "метод бесконечного спуска", которым так гордился великий Ферма.
Устанавливая ДОКАЗАННОСТЬ некоторого математического положения, мы фактически высказываем суждение о СУЩЕСТВОВАНИИ или НЕ СУЩЕСТВОВАНИИ.
Можно предположить, что принцип полной редукции не может не использовать ряда натуральных чисел, ибо только там мы можем ввести понятие - "НЕПОСРЕДСТВЕННО СЛЕДУЕТ ЗА". Однако аксиоматика натурального ряда должна быть представлена в форме, отличной от аксиоматики Пеано:
Существуют натуральные числа.
Каждое натуральное число имеет одно и только одно ПРЕДШЕСТВУЮЩЕЕ ЕМУ.
Натуральных чисел, которые меньше единицы, не бывает.
Эти определения отличны от грассмановского двустороннего ряда, так как при бесконечном спуске заканчиваются на той или иной "единице".
Нами получено корректное определение понятия "НЕПОСРЕДСТВЕННО ПРЕДШЕСТВУЕТ".
Само собою разумеется, что имеется множество работ, где говорится о единственности предшествующего элемента, но проблема состояла в таком обращении натурального ряда, чтобы не была потеряна эта КОНЕЧНОСТЬ при методе спуска.
Первая "проба пера" метода полной редукции и должна быть проведена на проблеме некоторого "НЕ СУЩЕСТВУЕТ'. Почти очевидно, что такое утверждение мы имеем в истории от самого Ферма.
Не имеет смысла обсуждать n+1 "доказательство" теоремы Ферма, если автор не может указать ошибок своих предшественников.
Этих ошибок три:
Подмена задачи Ферма - другой задачей (в частности, использованием иррациональных чисел).
Использование принципа "полной индукции", не имеющего силы для БЕСКОНЕЧНЫХ множеств (множество натуральных чисел - бесконечно).
Отсутствие проверки на четность из-за некорректного "определения" четного числа.
Я полагаю, что Ферма умел
использовать проверку на четность, которая утрачена в процессе развития
математики.
Метод, которым так гордился Ферма, известен как метод "бесконечного
спуска". При использовании этого метода признак числа, быть ЧЕТНЫМ или
НЕЧЕТНЫМ, сохраняется вплоть до самого малого элемента.
Это дает мне право утверждать, что "метод бесконечного спуска Ферма" - есть другое название проверки на ЧЕТНОСТЬ. Эта задача и была утеряна при поиске "доказательства".
Мы назвали три типичные ошибки в попытках "доказательства" теоремы Ферма. Остановимся на них более детально.
Типичным примером первой ошибки является введение иррациональных чисел, что связано с отказом от основной теоремы арифметики.
Так отказ от основной теоремы арифметики, в рамках которой и требовалось решать проблему, является подобным примером. Например, Г. Эдвардc пишет:
"Оказывается, среди математиков существует глубоко укоренившаяся тенденция неосознанно предполагать единственность разложения на простые.
Эта тенденция, несомненно, навеяна опытом вычисления с обычными целыми числами и той важной ролью, которую играет единственность разложения в доказательстве таких фактов, как утверждение о том, что произведение двух взаимно простых чисел есть квадрат только тогда, когда каждый сомножитель является квадратом" [1].
Нетрудно видеть, что
корень n-ой степени из суммы (хп+уп) - простой пример запрета на иррациональные
числа, но... лишь в доказательстве теоремы Ферма.
Данное утверждение Г.Эдвардса ясно показывает, что мы имеем дело уже с другой задачей, чем задача Ферма.
Если мы остаемся в рамках АРИФМЕТИКИ, то мы можем обнаруживать противоречие, если по разные стороны знака равенства стоят:
Натуральное число Ф не равно натуральному числу.
Простое число Ф - составному числу.
Четное число Ф - нечетному числу.
Я полагаю, что этих трех дихотомий вполне достаточно для доказательства теоремы.
Один мой знакомый математик, сообщивший, что теорема Ферма доказана для показателя степени более 100 000, не мог понять, что принцип полной индукции принципиально НЕ МОЖЕТ привести к успеху, так как он может использоваться лишь для КОНЕЧНЫХ множеств.
В силу названного
обстоятельства мы и исключаем "принцип полной индукции" из всех
возможных доказательств теоремы Ферма. Наличие этого порока в подходе к
доказательству никогда не позволит по отношению к БЕСКОНЕЧНОМУ количеству
натуральных чисел сказать - "других не может быть"!
Это я и называю второй ошибкой представленных доказательств теоремы Ферма.
Метод "бесконечного спуска Ферма" до сих пор не получил адекватного выражения в современной математической литературе, а именно он и является ключом к доказательству.
Фактически в распоряжении Ферма на нижнем уровне "бесконечного спуска" и находилась проверка на ЧЕТНОСТЬ.
Мы приведем некоторое утверждение по отношению к БЕСКОНЕЧНОМУ натуральному ряду, эквивалентное теореме Ферма, в форме:
"Теорема Ферма может быть неверна лишь для показателя степени, который является ОДНОВРЕМЕННО НАТУРАЛЬНЫМ, ПРОСТЫМ и ЧЕТНЫМ числом."
Очевидно, что другого натурального, простого и четного числа, кроме двух, во всей бесконечной последовательности натуральных чисел не содержится.
Если мы докажем это положение, то тем самым будет доказана и сама теорема Ферма.
Мы полагаем, что препятствием на пути доказательства теоремы Ферма служило некорректное определение ЧЕТНОГО числа.
Так числа 6 или 10 считаются четными, но после деления на 2, становятся нечетными. При методе "бесконечного спуска" такое некорректное определение четности исключается, через последующее ДЕЛЕНИЕ.
Выделяется класс БЕЗУСЛОВНО четных чисел.
Исходя из правила, что ИСТИННЫЙ математический объект не может изменять своего свойства, мы должны избавиться от этого некорректного определения.
Корректное введение понятия ЧЕТНОСТЬ и есть тот действительный вклад в развитие математики, ради которого и можно позволить себе заниматься этой проблемой, породившей неисчислимое количество "фермистов".
Поскольку в настоящее время требуется доказать теорему Ферма лишь для показателя степени, который является натуральным, простым и НЕЧЕТНЫМ числом, то справедливость нашего утверждения будет доказана, если мы будем рассматривать лишь оставшийся случай.
Известно, что из трех чисел (х, у, z), входящих в формулировку теоремы - два являются нечетными, а одно - "четным". Мы взяли выражение "четный" в кавычки, так как подобными "четными" является и 6, и 10.
Однако мы можем уйти от этой неопределенности, если будем рассматривать разложение чисел на простые сомножители. В этом случае имеющаяся в каждом разложении любая степень числа 2 не может исчезнуть и останется как признак ЧЕТНОСТИ.
В этом случае возможна проверка на "ЧЕТНОСТЬ", состоящая в том, что минимальный объект, сохраняющий четность, содержит в разложении на простые сомножители только число 2.
Допустим, что из трех натуральных чисел х, у, z где х < у < z число у является четным и пусть это число будет "минимальным" в методе бесконечного спуска. В этом случае у будет содержать в своем разложении на простые сомножители по крайней мере одно число 2.
В общем случае это может быть 2k.
Однако, ни х, ни z такого сомножителя не содержат.
Оставляяу в левой части равенства и перенося х в правую часть будем иметь:
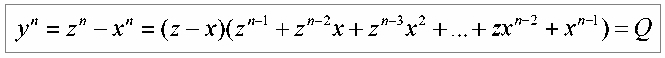
Желая избежать громоздких выражений, заменим сомножители правой части:
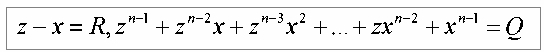
Теперь наше выражение примет вид:
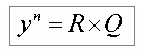
Поскольку мы ведем
доказательство для НЕЧЕТНОГО показателя степени, то следует обратить внимание
на то, что сомножитель Q - есть НЕЧЕТНОЕ число, поскольку он составляет
НЕЧЕТНУЮ сумму НЕЧЕТНЫХ чисел.
Здесь часто встречается ошибка, связанная с введением в эту сумму биномиальных коэффициентов, часто "переписываемая" от более ранних авторов.
Однако в первом сомножителе - R - разность двух нечетных чисел при разложении на простые сомножители даст число 2 в той или иной степени. Это можно записать так:
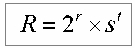
С другой стороны мы имеем слева ЧЕТНОЕ число без кавычек, которое можно представить как 2k. В этом случае имеем:
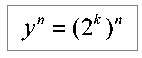
Сравнивая теперь левую и правую часть полученного выражения, находим:
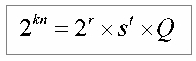
Здесь и наступает время проверки НА ЧЕТНОСТЬ:

В первом и третьем случае на основе различия ЧЕТНОСТИ теорема доказана. Во втором случае мы имеем слева единицу, а справа число, которое заведомо больше единицы.
Рассматривая
возможное доказательство, которое имел в виду Ферма, мы хотели обратить
внимание на важность принципа ПОЛНОЙ РЕДУКЦИИ, как "дополнительного
средства решения некоторых проблем.
|
Предложенное доказательство является своеобразным "отходом" от другой работы, где известный прием "спинорной линеаризации" [2] дает возможность решать множество "нелинейных" проблем, которые так портят жизнь в математических приложениях к практике. |
Этот же принцип полной редукции может пролить некоторый свет на решение шестой проблемы Гильберта, так как ставит вопрос о многообразии "физических" ЕДИНИЦ [3].
ЛИТЕРАТУРА:
[1] Г.Эдвардс "Последняя теорема Ферма". "Мир", М. 1980, стр.120.
[2] П.Г.Кузнецов, С.Б.Пшеничников "Спинорный метод решения систем нелинейных алгебраических уравнений". ДАН. 1985.Т.283 №5, с. 1073.
[3] P.O. Бартини, П.Г. Кузнецов "Множественность геометрий и множественность физик".
Москва, Серебряный бор 1994г.
Опубликовано:
В сб. "Моделирование динамических систем", Брянск, 1974, с. 18-29.
В сб. "Проблемы и особенности современной научной
методологии". Свердловск, 1979, с.55-65. 28 августа
В Издательстве «Серебряный бор»®, 1994, Издание автора П.Г.
Кузнецова Зак. №8/94. Тираж 100 экз.
Последнее обновление ( 07.10.2008 г. )