Механика живого неба.

Владимир Торопов.

http://www.ornithopter.ru/1/files/ndex10.html

Мускульный махолёт "Джордано", 1991 год.

 

Махокрылы и эфироиды в экспериментах

Рекомендуем всем, кто интересуется полетом и новыми принципами механики, кто заботится о Земле и Небе.

«Учение о том, как по земле ходить,
явлено тем, кто небо живым почитает »
из восточной мудрости

 

 

Владимир Михайлович Топоров
Станция Юных техников
отдела Народного образования г. Воткинска

 

 

Предисловие

Данная публикация кратко ознакомит Вас с нашей работой в области машущего полёта и механики принципиально новых механизмов - эфироидов, способных работать от взаимодействия с мировой материальной средой - эфиром, подобно тому, как это происходит в небесной механике.

Следует отметить, что наши утверждения базируются на реальных экспериментах и астрономических наблюдениях.

В данном случае речь идёт об эфирных двигателях, получающих энергию, подобно планетам и спутникам, из эфирных полей.

Речь идет и об эфирных движителях - механизмах, способных отталкиваться от эфира.

В области машущего полёта получены крылья, способные получать энергию из воздуха. Здесь имеется в виду внутренняя тепловая энергия воздуха.

Созданы и испытаны различные орнитоптеры, то есть аппараты, летающие с помощью взмахов крыльями, по-русски - махолёты. Слово "орнитоптер" в переводе с греческого означает "птицекрыл". Все аппараты и установки с машущими крыльями будем называть махокрылами. Сюда же можно причислить и летающих животных.

Исследованы многие закономерности машущего полёта.

Исследуем механизм взаимодействия махокрылов с эфирной средой.

Опыты проводились в условиях станции юных техников города Воткинска. Нам помогали иногда специалисты ракетного завода, в разной мере были задействованы его лаборатории, цеха и службы в течение десятилетий. Большую же часть работы выполняли и выполняют школьники, а иногда студенты, под руководством автора.

Пусть эта публикация частично будет ответом на письма тех, кому я не смог ответить.

Привет Ольге Бочаровой-Месснер, Натану Кронистеру, Славе Топтыгину, Владимиру Савову, Владимиру Сидорову, Владимиру Навицкому... Наши поздравления махолётчикам из Торонто! Вашими успехами мы любовались у новогодней ёлки. Привет всем, которые ЕСТЬ и которые БУДУТ.

О себе сообщаю, что в 1973 году окончил Казанский авиационный институт, работал в опытно-конструкторском отделе - занимался баллистикой и динамикой ракет. По вечерам руководил планерным кружком в школе-интернате. В 1978 году перешёл на постоянную работу в клуб юных техников завода.

Почтовый адрес: 427439 Россия, Удмуртская республика, г. Воткинск, ул. Верхняя , 1, клуб "Алые паруса". Тел.: (34145)5-24-91.

 

Содержание

 Предисловие

Часть 1. Махокрылы

Глава 1.Введение

1.1. О нестационарных явлениях

1.2. Работа с математической моделью махолёта

1.3. О присоединённых массах

Глава 2. Работа с махокрылами

2.1. Опыты смоделями

2.2. Махолёт "Истина"

2.3. Две подобные модели

2.4. Мускульные махокрылы

2.5. Модель "Петруша"

2.6 Махокрылы - ротоптеры

2.7. О работах Флюра Сабитова

2.8. Саморазгоняющиеся крылья

2.9. Механизм получения энергии из воздуха

2.10. Волнообразный полёт

2.11. Колеблющиеся крылья и гибкая задняя кромка

2.12. Орнитоптеры "Алабино" и "Азазель"

2.13. О вертикальном взлёте махокрылов

2.14. Размеры махокрыла и экономичность полёта

2.15. Саморазгоняющийся планер

Выводы по махокрылам

Часть 2. Эфироиды

Глава 3. Взаимодействие эфира с материальными телами

3.1. Об эфире

3.2. Обнаружение эфирного ветра отвесом

3.3. Центробежная сила с позиций эфира

3.4. Движение тел под действием центральной силы

3.4.1. Замечания о силе Кориолиса

3.4.2. Свободное движение

3.5. Эфирные движители – центроиды

3.5.1. Теоретическое обоснование

3.5.2. Опытное обоснование центроида

3.6. Инерция и инерцоиды–движители

3.7. Инерционные эфирные двигатели

3.8. Разгон диска падающим грузом

3.9. Свободное падение тел и гравитация

3.10. Гравитационные двигатели

3.11. Эфир и махокрылы

Глава 4. Движение небесных тел под действием эфира

4.1. Общие вопросы

4.1.1. О сопротивлении эфиром

4.1.2. О влиянии эксцентриситета орбиты

4.1.3. О гравитационной константе

4.2. Возмущающее действие эфира на движение Луны

4.3. Возмущения планет и роторный движитель

4.4. Вращение планет

Глава 5. Аномальные явления

Выводы по эфироидам

Фотоприложение

Заключительная часть

Список основной литературы

Часть 1 .Махокрылы

Глава 1.Введение

 1.1. О нестационарных явлениях

Руководство Воткинской школы-интернат (Ф. В. Камалеев и А. Н. Эртнер) в 1973 году предоставило мне возможность руководить школьным  техническим кружком. Ребята самых  различных классов занимались с увлечением.  Главной  нашей целью была постройка большого планера  «Демон» с размахом  крыльев 12,5 метров (фото 1, 2). Набираясь опыта по пилотированию, было пережито немало драматических событий. Но всё же он стал летать.

Однако, важнее другое – иногда он взлетал без разбега, с места. И случалось это тогда, когда натяжение резинового аккумулятора было сильным, когда резину натягивала большая группа ребят. При этом скорость разбега планера  при отрыве была почти нулевой. Подъёмная сила крыльев превосходила расчётную  (по формуле аэродинамики) во много раз. Это же можно наблюдать и при запуске моделей планеров.

Затем создавался клуб юных техников при профкоме завода. Организацией клуба  занималась молодая и энергичная Лариса Быстрова. При её постоянной поддержке мы построили самолёт  «Nansen» с мотоциклетным двигателем «Иж-пс», обрезав у него коробку передач (фото 3). Отработали деревянный воздушный винт, и самолёт  хорошо полетел. Затем отлили металлический воздушный винт  ( копия деревянного) – и он полетел хуже. Невозможно было понять: в чём дело?  Провели эксперимент на небольшом авиамодельном двигателе «КМД-2,5» - тот же результат: с деревянным винтом тяга больше. Но почему? Ответ пришёл не скоро.

Дело оказалось в том, что аэродинамические характеристики воздушного винта (а также и любого крыла) зависят от режима движения – от его характера. При установившемся режиме (с постоянной скоростью) аэродинамические характеристики (сила сопротивления и подъёмная сила) хуже, чем при неустановившемся  режиме (с переменными скоростями, с ускорениями). Движение с ускорением называют  ещё нестационарным  движением. Установившееся движение с постоянной скоростью потока воздуха относительно крыла – это стационарное движение.

При нестационарном  движении  воздушное сопротивление крыла  снижается, а  подъёмная сила – растёт!

Применим этот вывод к воздушному винту (нашего самолёта), который вращается  одноцилиндровым двигателем неравномерно – нестационарно. С деревянным винтом пульсации (ускорения) были в 5 раз больше, чем с металлическим винтом. Это и было причиной разницы в силе тяги двух винтов. Это и повышало силу тяги деревянного винта.

Позднее мы сделали модель аэромобиля с пульсирующим воздушным винтом, с приводом от резинового двигателя. Пульсации производились за счёт пружины, которая подцеплялась шарнирно к колену вала воздушного винта. При снятой пружине винт вращался без пульсаций. Сравнения двух этих режимов опять показали преимущество пульсирующего винта около 30 %.

Фото 1.

Фото 2. (Снимок поврежден, нет нижней половины)

Нестационарное движение планера «Демон» при разбеге повысило его подъёмную силу, что уменьшило скорость отрыва.

Опытные профессиональные лётчики рассказывали нам, что при большей силе тяги реактивного двигателя  скорость отрыва воздушного лайнера  уменьшается.

Ещё один пример – лёгкие самолёты конструктора из Киргизии В.Дмитриева  отличаются малым весом (54 кг), малой площадью крыла (1,76 м²), отрываются при скорости 55 км/час. Получается очень высокий коэффициент подъёмной силы С_у = 5 (но это только при разбеге). Дело опять в том, что двигатель сравнительно большой мощности разгоняет лёгкий аппарат со сравнительно большим ускорением – нестационарность обтекания повышает подъёмную силу.

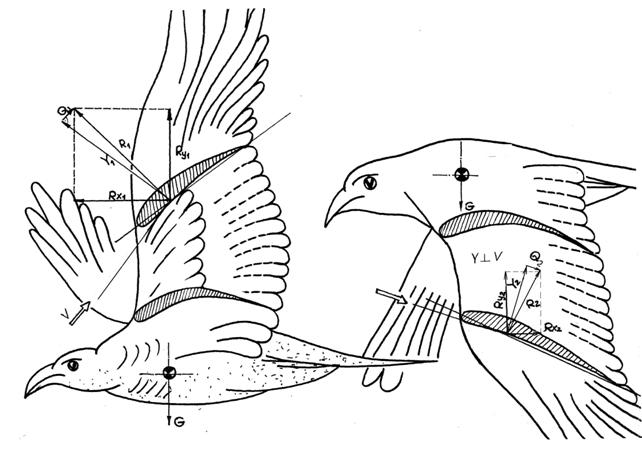
Этой нестационарностью пользуются  птицы и насекомые. Их крылья и корпус совершают пульсирующие движения, что даёт большие преимущества перед неподвижными крыльями. Коэффициент подъёмной силы  Су  чайки при взлёте с воды составляет 25 единиц. В наших опытах этот коэффициент достигал 12 единиц (с крыльями махолёта «Джордано»), а иногда - значительно больших значений. Например , при резком разгоне модели планера, изготовленного из сплошного дерева.

Нестационарным явлениям посвятили свою жизнь московские учёные Е.Д.Сорокодум, профессор МАИ В.А.Киселёв и другие исследователи. Они отмечают большое улучшение аэродинамики неустановившихся (нестационарных) течений.

Теперь имеет смысл поговорить об аппаратах с машущими крыльями.

Фото 3

 

1.2. Работа с математической моделью махолёта.

Создать математическую модель махолёта в реальном нестационарном потоке было невозможно. Тогда мы создали математическую модель для стационарного потока, воспользовавшись значениями аэродинамических коэффициентов (сопротивления С_х и подъёмной силы С_у) для конкретных профилей крыла, взятых из аэродинамических продувок. Крыло двигалось вверх и вниз  «параллельно», как у Рейфенштейна (см. список лит.-1), то есть передняя кромка крыла и лонжерон  поднимались и опускались параллельно самим себе. Мы приняли также: скорости и углы атаки крыла при подъёме и опускании постоянны, пульсации центра тяжести отсутствуют (рис.1).

В течение полугода было просчитано немало вариантов. Проведена первая математическая оптимизация параметров модели, построены графики. Например, наивыгоднейший угол подъёма крыла ₂  составил от 0 до 2 градусов, С_у^{подъёма} =0,5С_у^{опускания}_. Такую модель мы назвали волнолётом. Расчёты показали, что волнолёт способен лететь в условиях стационарности с коэффициентом полезного действия  в 95%, но при этом  ухудшаются несущие свойства планера нашего волнолёта – его аэродинамическое качество снижается на ~ 5%. В итоге, приведённый к.п.д. (_пр) получался равным 90%.

_пр =  , где:  =   ;       = - аэродинамическое качество планера махолёта (волнолёта),   _мах =  - аэродинамическое качество махолёта  ( волнолёта),   с - осреднённый (за период полного маха) коэффициент подъёмной силы,   - осреднённый коэффициент сопротивления,  - коэффициент несущих свойств махолёта.

И мы построили реальную модель волнолёта (фото 4) , соответствующую приближённо расчётной. Для привода крыльев применили резиновый двигатель, работающий на прямое сокращение посредством роликов. Пружинный аккумулятор запасал энергию резинового двигателя и воздушного потока при подъёме крыла; этот же аккумулятор служил и для получения нужного распределения скоростей подъёма и опускания крыла, а, следовательно,  и распределения углов атаки крыла. 

Модель пролетала  до 50 метров. Но! Фюзеляж модели трясло, привод крыла получался громоздким, силы инерции  были сравнительно большими, поскольку в вертикальном движении участвует всё крыло вместе с узлами привода.

Фото 4. Модель волнолёта

При этом мы занимались уже математической моделью нормального махолёта в соответствии со схемой сил на рис. 2. Я написал систему уравнений движения махолёта с применением двойных интегралов  (по размаху крыла и по времени). Инженер-программист Александра Жуйкова занималась решением и отработкой программы на заводе. Она довела её до совершенства. По заданным характеристикам (например, подъёмной силе) ЭВМ сама выбирала требуемые параметры махолёта, например, частоту махания или амплитуду, мощность привода и т.д..

Данная математическая модель позволила рассчитывать махолёты (орнитоптеры) с любым числом крыльев, с любым смещением фаз движения крыльев. Распределение вертикальных скоростей крыла по времени за период маха – синусоидальное, близкое к реальному. Распределение углов атаки по времени  – синусоидальное, наибольший угол атаки при опускании крыла, наименьший – при подъёме.

Но это была, по-прежнему, модель лишь при стационарном обтекании. Некоторые варианты расчёта представлены в таблице 1. Вариант 7 рассчитан для вертикального старта со скоростью подъёма 1 м/сек.

Приведённый к.п.д. с ростом скорости не падает, как это происходит у самолётов с воздушными винтами при околозвуковых скоростях. И этот к.п.д.  выше в ~2 раза, чем у любых современных лайнеров.

Как показал опыт дальнейшей работы с махокрылами, характеристики реального крыла в условиях нестационарности существенно превосходят расчётные, если движение элементов крыла выполнено с требуемым распределением углов атаки по размаху и амплитуде крыла. В отдельных случаях, как покажем далее, к.п.д. реального крыла равнялся бесконечности, то есть, совершалась работа крыла без подвода энергии привода. Крыло работало за счёт энергии окружающего воздуха.

 

 

Как показал опыт дальнейшей работы с махокрылами, характеристики реального крыла в условиях нестационарности существенно превосходят расчётные, если движение элементов крыла выполнено с требуемым распределением углов атаки по размаху и амплитуде крыла. В отдельных случаях, как покажем далее, к.п.д. реального крыла равнялся бесконечности, то есть, совершалась работа крыла без подвода энергии привода. Крыло работало за счёт энергии окружающего воздуха.

 

1.3. О присоединённых массах

По ходу работы с моделями проводились попутные эксперименты по удару крыльев, по определению присоединённых масс воздуха вокруг движущихся тел. Иногда эта присоединённая масса в десятки раз превосходила массу крыла (m_кр), например, при малых ускорениях плохо  обтекаемых тел (конкретный пример: пластина или плоскость крыла, расположенная к потоку под углом  ).

При постоянной силе разгона (F) ускорение () получается (кратковременно) постоянным, а сама присоединённая  масса  () определяется просто – по формуле второго закона динамики :    +=.

Время разгона, ускорения разгона и другие факторы существенно влияют на величину присоединённой массы.

Исследовалось поведение маятников в воде. Получалось различие присоединённых масс при горизонтальных и вертикальных колебаниях, независимо от объёма и глубины погружения маятника.

Обнаруживалась существенная разница присоединённых масс воздуха при горизонтальных и вертикальных разгонах пластины. При горизонтальном  разгоне сила сопротивления была меньше в 3  3,5 раза.

Присоединённая масса – это одно из проявлений нестационарного обтекания тел, в том числе, и махокрылов. Это понятие позволяет полноценнее усвоить картину обтекания машущих крыльев и их фюзеляжа.

Присоединённая масса помогает осознать механизм изменения инертной массы тела  под воздействием эфирной среды, например, при движении в безвоздушном пространстве        (см. часть 2).

Присоединённая масса машущих крыльев орнитоптера образуется за счёт воздуха и эфира, у подводных крыльев – за счёт воды и эфира.

2.3. Две подобные модели

Следующим шагом мы изменили схему и аэродинамику махолёта. Сначала построили лёгкую метровую модель «Встречная» весом 69 граммов с резиновым двигателем. Сила тяги крыльев превышала её полётный вес - она взлетала вертикально, летала стабильно по 22 секунды (один полёт длился 35 секунд). Внешне она походила на модель «Петруша»

(см. далее).

Затем мы изготовили подобную ей модель, размеры которой были увеличены в 4 раза. Получилась модель махолёта «Невидимка» весом 6 кг, с резиновым двигателем (фото 11-14).    Она взлетала с земли, пролетала 165 метров за 18,5 секунд. Её аэродинамическое качество равнялось 10.

Для горизонтального полёта ей требовалось 62 ватта мощности, модели «Встречной» - 0.83 вт. Скорости полёта отличались в 3,55 раза, вес отличался в 87 раз. Получалось, что полёт большой модели экономичнее в 4,13 раза. Экономичность Е_уд– это затраты энергии двигателя, отнесённые к единице пути S и к единице веса аппарата G :

Фото 11. Махолёт «Невидимка с резиновым двигателем

После энергетических замеров мы поставили на неё поршневой двигатель «КМД-2,5» с редуктором (от модели «Элона»), которые пришлось расположить поперёк фюзеляжа. В результате изменений аэрокачество снизилось до 6 единиц, а вес вырос до 7 кг. Но модель могла летать теперь продолжительно. В конце июля 1989 года мы повезли «Невидимку» на авиасалон в Ригу. В одном из запусков модель пролетала 4,5 минуты. При взлёте с земли разбег равнялся 60 метрам, затем его удалось уменьшить до 3 метров. Сила тяги на месте превосходила тягу крыльев «Элоны» более чем в 1,5раза.

Этот же двигатель с воздушным винтом развивает тягу на месте только до 0,5 кг (а в полёте - ещё меньше), что явно недостаточно для полёта данной модели в самолётном режиме с неподвижными  крыльями.

О полёте этой модели можно прочитать , например, в статье Ю.Егорова «Первый, который взлетел» (журнал ИР, №11 за 1989 год). Нам прислали статью Клавдии Сакалаускас из Литвы, которая со своими коллегами из их авиажурнала внимательно наблюдала весь полет.

У моделей «Встречная» и «Невидимка» каждое крыло «ударяло» вниз поочерёдно, через четверть периода, как и на многих других наших моделях.

Амплитуды махания крыльев обеих моделей - 10°.  

 

2.4. Мускульные махокрылы

В 1988 году  был изготовлен махокрыл «Надежда» для езды на велосипеде от мускульных усилий ног (фото 15). Цепь привода заднего колеса была снята. Крылья соединялись друг с другом  рессорным аккумулятором.

 Мы развивали на нём скорость до 20 км/час. Тяга на месте доходила до 6 кг – можно было катиться по травяному полю. Это при амплитуде махания  ±10°, при большей амплитуде тяга была меньше, так как не развивалась мощность мускулов, а крыло закручивалось меньше из-за меньшего момента силы привода.

Был получен дымовой спектр обтекания машущих крыльев. Поток воздуха обтекает махолёт иначе, чем привычные аппараты (самолёты и планеры). Поток идёт от фюзеляжа вдоль крыла  - это снижает сопротивление фюзеляжа. Другой поток идёт от конца крыла к центру – это ликвидирует индуктивное сопротивление крыла. Два эти потока встречаются и выбрасываются назад, создавая подобие реактивной струи (рис. 5а). Эта приближённая картина обтекания подтверждается наблюдениями за другими аппаратами, а также экспериментами Е.Сорокодума с птичьим пером и исследованиями структуры крыльев насекомых энтомолога О. Бочаровой-Месснер.

Фото 15. Испытания машущих крыльев от мускульных усилий ног

рис. 5а

1990 году мы построили мускульный махолёт «Джордано» (фото 16 - 19).

Его крылья работали, как и у «Элоны», в противофазе, качаясь относительно горизонтальной оси в центре, правая половина крыла жёстко соединена с левой. Крылья упруго закручивались от воздуха, а точнее – от шести систем сил: аэродинамических, инерционных, привода, жёсткости на кручение, жёсткости на изгиб, веса.

В полёте сила инерции крыла  «Джордано» (при торможении крыла) полностью компенсировалась аэродинамической подъёмной силой – стоило только вовремя  ослабить напряжение мускулов.

Махать крыльями в полёте было легче, чем на земле без продольного движения.

Амплитуда махания зависела от хода ноги и составляла, в среднем, 1 метр (±0,5 м). Ноги двигались в противофазе взад-вперёд.

Проводили испытание с принудительным закручиванием консолей крыльев от привода. В этом случае применялся велосипедный привод – ноги двигались как у велосипедиста по кругу. Это требовалось для синхронизации фаз махания и фаз закручивания.крыла.

Размах крыльев – 12 метров, площадь – 14 м², удлинение l=20. Вес конструкции – 63 кг.

Испытывали и дорабатывали его 5 лет, летом и зимой. Сотни подлётов и пробежек. По травяному полю аппарат не мог катиться за счёт своей тяги – мы поднимали его на буксире. Но три выезда своим лагерем имели цель самостоятельно оторваться от асфальта, без буксировки. И вот однажды, основные колёса тоже оторвались от дороги. Был отрыв – небольшой, плавный, при скорости  32,5 км/час, при полётном весе 135 кг. Отрыв подтвердили Андрей Смольников и Алексей Стерхов – наши замечательные кружковцы.

Отметим, что скорость отрыва махолёта значительно зависит от частоты и от амплитуды махания крыла. От этих же параметров зависит и развиваемаая пилотом мощность. Она в наших опытах не могла быть максимально возможной для человека, особенно, при большой амплитуде махания, которая наиболее выгодна с точки зрения аэродинамики. И здесь нужен редуктор для оптимизации полёта. Нам же приходилось  ограничиваться либо очень малыми амплитудами, либо сравнительно небольшой мощностью пилота.

Аппарат после отцепления на высоте около 0,5 метра пролетал по 200 ... 300 метров, но это случалось редко. Задняя центровка аппарата не обеспечивала устойчивого полёта, много внимания уделялось пилотом (автором) управлению, наблюдением за работой органов аппарата, часто кренило влево из-за конструктивных ошибок в одном крыле.

 3 апреля 1991 года при ветре 5-7 м/сек (было пасмурно) мне удалось продержаться в воздухе  на малой высоте около 40 секунд. При махании аппарат резко набирал высоту, я прекращал махи – аппарат снижался, опять махал – опять резкий подъём. И так - 3 раза. Налицо – расхождение центровок при машущем и планирующем режиме полёта. Но радовало то, что тяги вполне хватает. Этот полёт я прекратил сам, совершив хорошую посадку. Дальность свободного полёта мы замерили – около 200 метров. Испытания проводились на снежно-ледяной поверхности пруда.

Начальная высота полёта после отцепления от буксира – снегохода в этом опыте составила 0,6 метра (определили по первому фотоснимку Лены Зориной). Конечная скорость, примерно, равнялась начальной скорости аппарата и имела значение 40 км/час. Перед моими глазами на стойке пилона был установлен самодельный лепестковый датчик скорости воздушного потока. Скорость буксировки при отцеплении троса определялась также водителем снегохода Винером Сайгофаровым. Ему была дана установка на заданную скорость с учётом средней скорости ветра на данный момент.

В этот же день мы оценили аэрокачество махолёта по планированию с высоты 6 метров. Оно составило, примерно, 30 единиц.

Позднее мы выяснили причину изменения центровки (перебалансировки аппарата) с помощью модели «Петруша». Для устранения недостатка следовало увеличить угол установки задних крыльев. Это повысило бы и общую устойчивость аппарата за счёт смещения центра давления крыльев назад. Но, к сожалению, мы этого не сделали на «Джордано».

Своё впечатление от этого полёта написал в местной газете Андрей Поздеев с приложением фото (заметка сохранилась). На испытании присутствовал Владимир Крылов, но он был только с фотоаппаратом. Фотолюбитель Сергей Анфиногенов неспешно сделал 4 фотоснимка.

Фото 16. «Джордано» в свободном полёте

21 июля 1991 года уже темнело, и, вдобавок, сломался буксировочный замок на аппарате. Но мы все почувствовали, что аппарат подаёт хорошие надежды. Не вдаваясь в подробности, мы быстро (пока не выпала  роса) привязали буксировочный фал (капроновый шнур) одним концом за рессору автомобиля, другим – за нос махолёт. И мы тронулись, непрерывно  махая крыльями от начала и почти до самого конца опыта. Аппарат при буксировке поднялся на высоту человеческого роста, пролетел на одной высоте несколько мгновений (1 или 2 секунды) и фал ослабился.  Затем я быстро стал догонять буксировщика, постепенно выкручивая ручку высоты «от себя» (на пикирование). Мы с махолётом  обогнали автомобиль несколько слева и  немного улетели вперёд. Аппарат летел уверенно, легко волоча за собой шнур. Впереди приближалась река Сива. Я вынужден был сделать посадку у  берега, для чего резко спикировал с высоты около 4 метров. Точнее, сначала аппарат стал проваливаться, поскольку я перестал махать и за счёт этого необыкновенно резко упала подъёмная сила и  произошла перебалансировка (на пикирование). Я его выровнял, хотя и с опозданием (при посадке погнулись оси колёс, серьезных повреждений не произошло).

Испытание проводили на ровном поле – без уклонов. За всем этим пролётом внимательно наблюдали кружковцы и потом все мы до глубокой ночи рассказывали, уточняли разные подробности.

Воздушная скорость отрыва аппарата – около 40 км/час, скорость аппарата относительно земли в конце машущего полёта – около 60 км/час.  Длина буксировочного фала – 60 метров. При испытании дул встречный ветер 2-3 м/сек. Педали двигались взад-вперёд. Частота хода педалей и махания – 1.5 герца. Так получилось, что о других данных полёта можно говорить лишь весьма приближённо, особенно, о времени полёта (мы его не засекли.).Дальность полёта (замеров своевременно не произвели) значительно превосходила ту, которая была получена  в  опыте от 3 апреля, а время полёта – меньше, чем тогда.

Мы ещё раз убедились, что аппарат при постоянном махании значительно устойчивее, чем при переменном режиме полёта (с махами - без махов). Мы ещё раз убедились, что машущие крылья могут очень хорошо тянуть на скорости.  

Усилия ног на педали были мало ощутимы. Возможно, я просто этого не заметил, уделяя основное внимание устойчивости аппарата и другим вопросам. Помню, что мне хотелось лететь дальше, но, к счастью, я не забыл, что «привязан». Когда мы остановились, то расстояние между аппаратом и автомобилем составляло около  30 метров.

Получив какие-то результаты, мы меняли параметры аппарата, режим полёта,  условия… Это далеко не всегда приводило к ожидаемому успеху. Но мы получали информацию для сравнения.

Фото 17. «Джордано-3».Только с одной парой крыльев, правое полукрыло жёстко соединено с левым полукрылом. Так летают иногда альбатросы.

Фото 18. «Джордано –2» в конце пробежки. Была получена скорость 34 км/час.

Фото 19. Испытание «Джордано» на буксире за автомобилем.

«Джордано» испытывался с разными амплитудами махания, с различной жесткостью крыльев. У него менялась схема привода, вводилось управление по крену и принудительное закручивание консолей крыльев от привода. Исследовалось влияние щелей между передними и задними крыльями на силу тяги. Исследовался способ махания набегающим потоком воздуха при перекашивании крыльев (Джордано-3, фото 17). Замерялась подъемная сила при стоянке на месте, при различном ветре. Производилась приближённая оценка аэродинамического качества, которое менялось в наших опытах в диапазоне от 20 до 65 единиц в зависимости от метеоусловий и других факторов. У него менялась схема – он испытывался и в двукрылом варианте (Джордано-2, фото 18).

Практически на всех махолетах мы исследовали вопрос о том, как изменяется сила тяги с ростом скорости аппарата. На моделях эта тяга вначале росла, при дальнейшем увеличении скорости -  падала. На «Истине» - тяга падала, а вот на «Джордано» - она росла!

О мускульном махолёте «Азазель» будет рассказано отдельно, далее.

 

2.5. Модель «Петруша»

Модель махолета «Петруша» с резиновым двигателем (фото 20) изготовлена Алексеем Хворенковым и Алексеем Ложкиным в 1992 году. У нее, в отличие от других моделей, коленвал привода расположен сверху от крыльев – это изменило распределение ускорений по амплитуде махания, наибольшие ускорения здесь получаются, когда крыло внизу. Исследовалось также влияние амплитуд махания на развороты модели – при увеличении амплитуды правого крыла модель шла влево. Модель весит 240 граммов и развивает тягу, равную своему весу! Было выявлено существенное влияние установочного угла задних крыльев на аэродинамику модели – при увеличении этого угла на 3^о (по отношению к углу передних крыльев) улучшено аэрокачество на 25%, повысилась устойчивость модели. К сожалению, мы не применили этого приёма на «Джордано», эти результаты от «Петруши» были получены в конце 90-х годов, после прекращения работы с «Джордано».

Важно также, чтобы задние крылья располагались ниже передних – это тоже результат  экспериментов.

Фото 20. Махолёт «Петруша», слева – в 1992 году, справа – в 2004 году.

 

2.6. Махокрылы – ротоптеры

Ротоптеры – это аппараты, у которых крылья машут и движутся по кругу относительно вертикальной оси (по определению Владимира Савова из Болгарии). Махокрыл «Влади» создан с целью отработки вертикального старта. Вес конструкции – 28 кг, размах крыльев – 10 м (фото 21).

При вертикальном перемещении втулки крылья машут, и от возникающей силы тяги разгоняются. Оба крыла соединены в центре шарнирно и поднимаются (или опускаются) одновременно, как у птицы.

Аппарат несколько раз отрывался от земли при скорости вращения 0,45 оборота в секунду. После отрыва аппарат вёл себя, конечно, неустойчиво – здесь требуется дополнительная отработка. В связи с этим, допускались отрывы небольшие – до 15 см. Но моей мощности вполне хватало для отрыва, естественно, после долгих настроек, регулировок, переделок.

Регулирование угла атаки крыла производилось пружиной, соединяющей заднюю кромку крыла с вертикальной осью крыльев. Поворачивалось всё крыло (оно почти жёсткое) под действием всей системы сил – углы установки при этом менялись, обеспечивая тягу и подъёмную силу.

Достоинством ротоптера является то, что крылья здесь можно делать жёсткими, поскольку угол наклона вектора скорости одинаков во всех сечениях крыла по размаху. Значит, и угол установки b можно делать везде одинаковым.

В нижнем положении крылья пришлось тормозить пружинками, чтобы происходил нужный поворот крыльев относительно продольной оси крыла  z.

Подкосы крыльев жёсткие, с обтекателями из дерева (в последнем варианте).

Важной задачей являлось – снижение пульсации подъёмной силы у двукрылой птицеподобной схемы. Испытания «Влади» дали опыт в этом вопросе.

Для получения большей информации такой аппарат следует размещать на жёсткой вертикальной оси, чтобы он мог «висеть» в воздухе сколько угодно без ухода в сторону. Сразу полететь не удаётся. Быстрее полетим, действуя последовательно.

Фото 21. Аппарат «Влади» и его конструкторы

Модель ротоптерного типа  «Феофан» с резиновым  двигателем весит 60 граммов      (фото 22).  Эта модель могла висеть в воздухе до 20 секунд – до полной раскрутки резины. Она могла взлетать при первом же ударе крыла, то есть без разбега крыльев. Модель запускалась на вертикальной проволоке, по которой модель могла скользить.

Изготовил модель Саша Корякин. Ему помогал Эдик Лопатин. Саша демонстрировал и защищал эту модель на гагаринском конкурсе в Звёздном городке под Москвой.

Все 4 крыла приводились в действие от одного колена проволочного вала, но работали  в разных фазах.  После увеличения амплитуд махания от 10° до 20° висение стало более продолжительным (с тем же резиномотором).

Здесь подъёмная сила одного крыла регулировалась (уравновешивалась) подъёмной силой противоположного крыла через вал, на котором они были жёстко закреплены. Этот вал мог качаться для махания и мог ещё вращаться за счет большого люфта – зазора оси качания для регулировки углов установки b.

Таким образом, у данной модели отсутствуют потери энергии на удары, и производится автоматическое регулирование подъёмное силы. Здесь подъёмная сила крыла постоянна. При этом развивалась и хорошая сила тяги крыльев, за счёт которой они двигались по кругу. Тяга возникала за счет нестационарности потока – в связи с поворотом крыльев. При стационарной модели обтекания тяга крыла в этом случае должна равняться нулю, поскольку углы атаки крыла при его подъёме и опускании равны.

Чертежи этой модели, а также «Элоны» и «Истины» хотят напечатать в альманахе по махалётам, который готовят к изданию в Самарском авиационном институте. Они подготовили материалы о пятистах конструкциях с машущими крыльями.

 

 

Следующий аппарат ротоптерного типа «Лузениана». По принципу работы крыльев – это большой «Феофан». Но здесь только одна пара крыльев, которые машут от  усилий ног и рук (фото 23, 24). Внизу расположены пружины для аккумулирования энергии ударов крыла. Одно крыло жёстко соединено с другим посредством вала.

Было получено быстрое вращение крыльев – один круг за 1,5 секунды при малых установочных углах b, подъёмная сила крыльев – 30 кг, которая замерялась специальным датчиком, на который ставился весь аппарат. Всё это было смонтировано на жёсткой вертикальной оси, вокруг которой всё вращалось, вместе с человеком. Здесь не была доведена до конца оптимизация подъёмной силы – следовало ещё больше увеличивать углы хода крыла Db за счёт увеличения зазоров между валом и осью качания, по аналогии с работой над «Феофаном». Диаметр ротора сделали больше, чем на «Влади», на 2 метра, увеличили амплитуды махания. Всё это заметно снизило частоту махания, подводимую мощность и тягу крыльев. 

Фото 23.

Фото 24.

 

2.7. О работах Флюра Сабитова

В 70-х годах он занимался в нашем кружке в школе – интернате, строил планер «Демон», позднее активно участвовал в постройке махолётов «РМ – 4», «Невидимка», «Истина», разрабатывал и успешно запускал свои лёгкие модели с машущими крыльями.

 Позднее он организовал свою лабораторию на базе КСТТ (клуб самодеятельного технического творчества), стал строить махолёты  двукрылой птицеподобной схемы. Большое число Рейнольдса, возможность получения более правильного удара крылом по воздуху (с ускорением вниз) привлекают внимание к этой схеме. Но больший вес крыла, больший момент инерции крыла, больший вес редуктора и привода, необходимость в аккумуляторе энергии, колебания корпуса при взлёте - отталкивают, если сравнивать с четырёхкрылой схемой, например, «стрекозой». И только практика подскажет: что лучше? Природа же пока указывает на птиц – большие животные летают с двумя крыльями.

Фото 25. (копия из местной газеты «Ленинский путь»).
Флюр пилотирует свой мускульный махолёт.

Фото 26.

В 90-х годах Флюр строит и испытывает махолёт с мускульным приводом (фото 25–27).    Крылья приводятся в действие от одновременных усилий обеих ног «от себя». Площадь крыльев около 18м², профиль крыла имеет большую кривизну в центральной части. Аппарат с человеком отрывался от земли при скорости 30 км/ч, при буксировке. При лёгком ветре его отрывали от земли два человека, двигаясь с ускорением. На нем выполнялись различные подлёты, вырабатывались навыки в управлении. Однажды за один вечер Флюр выполнил шесть полётов с высоты 10 – 12 метров, с махами и без махов. При этом дальность полёта отличалась в 2 – 3 раза, хотя махал он не всё время, уделяя внимание устойчивости аппарата. Амплитуда взмахов была очень мала (±2°).  С учётом этого, махолёт подавал хорошие надежды. Не обходилось без поломок, ему помогали его друзья Андрей Туров, Владимир Варламов…

Позднее Флюр построил моторный махолёт (фото 28-29). Для привода крыльев использовалась двигательная установка от «Истины». Аппарат разгонялся до 30 км/ч, приближался к отрыву, но сильная тряска от движения крыльев заставляла прекращать разгон. Необходим был механизм регулирования подъёмной силы. Флюр стал работать в этом направлении, но прекращение элементарного финансирования остановило пока его поиски.

Фото 27.Флюр производит лётные сравнения, Лето 1994.

Фото 28. Пробежки по торфяному полю при средних оборотах двигателя за счёт тяги крыльев.

Фото 29. Воткинские махолётчики у моторного орнитоптера Флюра, он – третий справа.

 

2.8. Саморазгоняющиеся крылья

Мы неоднократно замечали, что крылья махолёта «Джордано» способны иногда создавать силу тяги без подвода к ним энергии, то есть без двигателя. На сильном ветру, когда мы хотели их «продуть» на ровной площадке, они устремлялись вперёд, против ветра. В другой раз, в другом месте, замерили эту тягу – она равнялась 0,5 кг на одно крыло.

Определили аэродинамическое качество «Джордано», сопротивление фюзеляжа с хвостом  - получалось опять то, что крылья могут иметь отрицательное сопротивление (при  наиболее благоприятных атмосферных условиях, при небольших углах атаки).

Затем мы стали крутить крыло вокруг столбика (рис.5). При установившемся движении крыло тормозилось, но при волнообразном полёте, оно шло вперёд само и разгонялось. Я бегал вокруг столбика и касался правой рукой только шнурка, привязанного к задней кромке крыла в точке а, чтобы управлять углами поворота крыла относительно его продольной оси.

Опыты проводились при ветре и без ветра в полный штиль, зимой и летом, с утяжелением крыла (подвешивался груз) и т.д.

На последней установке «Лилиенталь» (фото 30) человек двигался вместе с крылом. Летом крыло тянуло как угодно долго, меняя скорость по моей команде – то меньше, то снова больше, есть видеозапись. Зимой этого не получалось – после предварительного разгона крыло проходило не более двух кругов, с ветром и без ветра. Следовательно, главную роль здесь играл не ветер.

Восходящие термические потоки у земли очень слабы, лишь на высоте 50 метров они достигают скорости около 0,5 м/сек. Наши наблюдения на нашей рабочей площадке не обнаружили существенных восходящих потоков (на протяжении многих лет). Получается, что и потоки не могли быть причиной саморазгона крыльев.

При загружении крыла  дополнительным весом, равным весу крыла, саморазгон крыла шёл эффективнее. Проводились опыты по загружению крыла подкосом с пружиной.

В сентябре 2004 года крыло само махало на ветру (без вращения по кругу). Получена тяга в 2 кг. Без ветра также получена сила тяги крыла, но меньше – 0,4 кг. Это, в какой-то мере, можно проверить с обычным крылом  с хорошим аэродинамическим качеством.

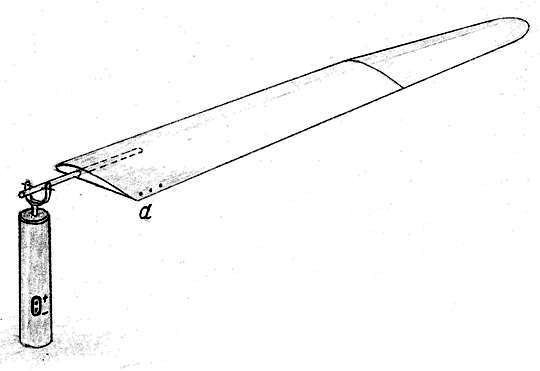
Рис. 5. Крыло-двигатель, в машущем режиме движется за счёт теплоты окружающего воздуха

Фото 30. Установка «Лилиенталь» с соморазгоняющимся крылом. . Видеофайл toporov.avi

 

2.9. Механизм  получения энергии  из воздуха

а) цилиндром:

Чтобы сжать воздух поршнем в цилиндре, требуется работа А. Воздух  при адиабатическом сжатии  нагреется, его внутренняя энергия  U повысится, при этом DU=А (из курса физики). Если теперь охладить воздух в цилиндре до начальной температуры, применив теплоту для чего-нибудь полезного, то оставшееся давление в цилиндре окажется больше начального давления. То есть, воздух в цилиндре ещё способен совершить работу А₁ (тем большую, чем больше степень сжатия).

Таким образом, общая энергия, полученная из воздуха, будет больше затраченной работы:  А₁₊ DU > А , т.к. DU=A . Налицо возможность получения  энергии из атмосферного воздуха. Второй закон термодинамики здесь не нарушается – тепло нигде не переходит от холодного к горячему.

б) крылом:

Двигателем, преобразующим тепловую энергию воздуха  в механическое движение крыла, является вихрь. Саморазгон вихря происходит в связи с понижением давления воздуха внутри вихря при его формировании за счёт центробежных сил, возникающих при движении частиц воздуха по кругу. С понижением давления понижается и температура (в соответствии с  объединённым газовым  законом). Куда же делась теплота воздуха? Она превратилась в кинетическую энергию упорядоченного движения частиц воздуха – скорость частиц выросла, поэтому  вырастут и центробежные силы – давление внутри вихря упадёт ещё сильнее. Процесс повторяется и усугубляется. Идёт также подпитка теплом окружающего воздуха путём теплопередачи за счёт разницы температур внутри вихря и вне вихря. Вихрь саморазгоняется! При этом температура окружающего воздуха падает. Нами производились замеры температуры вокруг крыла; моряки-исследователи, оказавшиеся внутри природного вихря, наблюдали понижение давления и температуры; после прохождения вихря температура океана понижалась на 2° (согласно данных журнала «Циклоны и антициклоны» из подписной серии «Метеорология, изд. «Знание»). Заметим попутно, что на принципе работы вихря можно будет делать и холодильники. Возможно совмещение двигателя с холодильником.

Получение силы тяги:

В аэродинамике доказывается, что интенсивность разгонного вихря определяет величину подъёмной силы крыла. Но! Чем больше подъёмная сила машущего крыла, тем больше и сила тяги крыла, в соответствии с математической моделью махолёта.

Во-вторых, присутствует эффект «отталкивания» вихрей от машущего крыла, обоснованный профессором В.В.Голубевым, в соответствии с теорией присоединённых и сбегающих вихрей. Но и машущее крыло «отталкивается» от вихря (по принципу действия и противодействия). Механизм «отталкивания»  крыла раскрывается в том, что за счёт присоединённых вихрей возникает разница давлений в передней и задней частях профиля крыла.

Многие эксперименты свидетельствуют, что эффект «отталкивания» присутствует и у колеблющегося крыла (без махов), когда сечение крыла совершает только повороты относительно его продольной оси z, например, относительно переднего лонжерона или передней кромки крыла.

Таким образом, вихри превращают теплоту воздуха в механическое движение крыла или махолета. На этом принципе можно будет строить энергостанции там, где есть атмосфера.

Обычные планёры, самолёты, вертолёты, авиамодели, воздушные винты – все используют внутреннюю энергию окружающего воздуха, в разной мере.

В самом деле, для удержания в воздухе реального планёра (весом 140 кг, при аэродинамическом качестве в 60 единиц, при размахе крыльев в 12 м, при скорости полёта  13 м/с) требуется мощность двигателя (планёру – мощность притяжения Земли) всего 298 вт. С другой стороны, чтобы получить нужный импульс подъёмной силы, необходимо отбросить вниз массу воздуха, для чего потребуется мощность двигателя 3714 вт. Это в 12,5 раз больше, чем потребляемая в действительности мощность. При меньшем аэрокачестве эта цифра будет меньше, но любом случае она внушительна.  В данном примере с планёром 1 часть энергии крыло получает от двигателя (земное тяготение), а 11,5 частей – от окружающего воздуха посредством вихрей.

Альбатросы, обладая хорошим аэрокачеством, способны получать из воздуха всю энергию, необходимую для полёта, даже при неподвижных крыльях (при благоприятных метеоусловиях). Альбатросов видели моряки в тихую погоду вдали от берега на сотни километров: «…крылья их были мертвы, как будто из мрамора».

Инженеры – аэродинамики обнаруживают (1) разницу в определении подъёмной силы по формуле Жуковского и по механике Ньютона (импульсным методом). Эта разница – иногда в десятки раз. Причина расхождения та же –  в создании циркуляции воздуха вокруг крыла участвует энергия воздуха; циркуляция же входит в формулу Жуковского. Поэтому эта сила, наиболее реальная, больше силы по  механике Ньютона. 

 

2.10. Волнообразный полёт

Им пользуются многие мелкие птицы (воробьи, ласточки, трясогузки…). При подъёме они машут, при снижении – складывают крылья. Однажды нам приходилось наблюдать, как многие тысячи стрекоз летели в таком режиме, все они летели в одном направлении, откуда вскоре пришла сильная гроза. Сорока тоже использует такой способ полёта. Вероятно, они это делают для улучшения аэродинамики.

Но, предположительно, есть и другая причина – изменение веса тела за счёт вертикальных перемещений. Имеется в виду: уменьшение веса при подъёме, увеличение – при снижении. В этом случае махокрыл получит энергию гравитационного поля. Об изменении веса тел, об отклонении от закона всемирного тяготения будем говорить во 2 части данной публикации (о механике эфира).

Мы оценили также специфичный  волнообразный полёт моторной авиамодели воздушного боя. В одном случае модель летала (по кругу) горизонтально без подъёмов и опусканий, в другом случае – волнообразно, то есть, с подъёмами и снижениями. В итоге, получилась разница. При волнообразном полёте модель летела с большей скоростью, в среднем, на 20%. Учитывая низкое аэрокачество таких моделей, получился неплохой эффект.

Хотелось бы, чтобы подобное сравнение провели пилоты самолётов, планеров, дельтапланов, радиоуправляемых моделей.

Причиной улучшения аэродинамики здесь является, во-первых, пульсация продольного движения (снижается сопротивление всего летящего объекта), во-вторых, поворот плоскости крыла относительно его продольной оси – колебательный эффект, подобный эффекту рыбьего хвоста (создаёт силу тяги), который характерен для полёта модели воздушного боя. Но! для усиления этого эффекта необходимо, чтобы центр поворота проходил ближе к передней кромке крыла, то есть, самолёту лучше иметь переднюю центровку.

При пульсации углов атаки, к тому же, возрастает подъёмная сила.

 

2.11. Колеблющиеся крылья и гибкая задняя кромка

При повороте крыла относительно его передней кромки возникает сила тяги, как в воздухе, так и в воде, как на месте, так и в движении.

В судомодельном кружке нашего КЮТ  по моей просьбе под руководством Александра Ускова была изготовлена модель корабля с колеблющимся крылом от электродвигателя  мощностью 12 ватт. Небольшое крыло площадью 30 см² создавало силу тяги в 320 граммов и двигало почти метровую модель со скоростью 1,2 м/сек. Вес модели – около 3 кг.

Затем применили колеблющиеся крылья на плоту. Крыльев было уже два – для снижения вибраций корпуса (фото 39). Они давали лучшую тягу, чем вёсла, приводились в действие руками.

С тем же двигателем, что и на модели корабля, сделали и испытали крыло, колеблющееся в воздухе, увеличив размеры крыла в 3,8 раза. Получили тягу в 60 граммов. В воздухе потери на удары оказались велики – следовало применить четырёхкрылую схему, как и на наших махолётах  типа «стрекоза».

Больших успехов в работе с колеблющимся крылом достигли москвичи А.И.Болдырев и П.А.Солодов (2). Их бензиномоторная модель с колеблющимся предкрылком взлетала с земли и достигла продолжительности полёта более 3 минут.

Стрекозы прибегают иногда к висению на месте за счёт только одних колебаний без махов. Мы наблюдали такое висение, при этом слышно было шуршание (трепет) крыльев. Этим интересным способом висения пользуется и пустельга. Полёт без махов, но с колебаниями мы называем колеблющимся полётом, а иногда – шуршащим.

Мы изготовили метровую модель планера, у которой крыло совершало автоколебания относительно оси, расположенной вдоль передней кромки крыла. В таком режиме планер летал дальше на 15%, чем  с неподвижными, «мёртвыми», крыльями.

Затем, вместо колеблющегося крыла, стали экспериментировать с гибкой задней кромкой крыла на моделях и на больших аппаратах (фото 31). Различные сравнения на моделях показали преимущества крыла с гибкой кромкой на ~20%. Каркас гибкой задней части крыла чаще делали из бамбука. Навёл нас на эту идею известный аэродинамик А.А. Борин, рассказав об уникальных профилях крыла лётчика Н.Фадеева, которые он исследовал в аэродинамической трубе перед войной.

В последнее время мы изготовили мускульный махолёт «Азазель», крылья которого могут совершать колебания-повороты относительно своей продольной оси на ±10 градусов за счёт усилий руки (или в автоматическом режиме при махах).

 Проведены опыты, получена тяга до 1кг (за счёт только колебаний) при наличии скоростного напора воздуха до10 м/сек. (фото 75).

Фото 31. Модель планера с гибкой задней кромкой крыла, рядом (спереди) лежат аналогичные крылья без гибкой кромки. Крылья взаимозаменяемые.

2.12. Орнитоптеры  «Алабино»  и  «Азазель»

Модель «Алабино» создана с целью изучения двухкрылой птицеподобной схемы       (фото 32, 33).  Её полётный вес с шасси – 122 грамма,   вес шасси -12 гр.,  вес крыльев – 24гр,

 площадь крыльев – 13,2 м²,  удлинение крыла l=9, размах крыльев – 1,09 метра; двигатель – резиновый, весом 24 грамма; коэффициент продольной устойчивости – 1,05, коэффициент устойчивости по курсу – 0,03, средний угол V-образности - 6^o, угол махания  y=±30^o (следует уменьшить до 20^o), частота махания  в горизонтальном полёте ~ 1,6 герца.

Крыло в плане имеет форму крыла фрегата (морская птица): центральная часть имеет отрицательную стреловидность, консольная часть крыла – положительную. Эта схема крыла показала преимущества (по устойчивости и по сопротивлению) на наших реальных моделях планеров.

Этот махолёт  отрывался от земли, при сильном закручивании резины он отрывался от пола при первом взмахе крыла – без разбега.

На модели установлен аккумулятор из резины весом 0,5 грамма, который при ходе крыла вверх вытягивается, а при ходе вниз – сокращается.

Полёт данной модели оказался экономичнее, чем полёт аналогичных моделей четырёхкрылой схемы («Встречная», «Петруша»).

Полёт модели происходит ровно, вертикальные колебания фюзеляжной рейки (корпуса модели) невелики и составляют около 5 % от полной амплитуды махания конца крыла (при полёте без шасси). Эту величину, вероятно, удастся снизить (при необходимости) после изучения гистерезиса подъёмной силы по углу атаки крыла. Его суть в том, что при увеличении углов атаки крыла (при его опускании) подъёмная сила не соответствует истинному углу атаки – она запаздывает и имеет меньшее значение. При подъёме она тоже запаздывает и имеет большее значение. Величина гистерезиса зависит от конструкции и режима движения крыла. Быть может, кто-то получит и обратный эффект, но полёт модели «Алабино» и его анализ свидетельствуют о прямом (положительном для нас) эффекте гистерезиса.

Недостатком  «Алабино» является то, что аккумулятор может быть настроен лишь на какой-то определённый вращающий момент двигателя, в то время как двигатель раскручивается с переменным моментом  силы вращения. Этот фактор уменьшает время полёта резиномоторного махолёта – наилучшее время полёта «Алабино» равно пока 20 секундам. Но это не принципиальный недостаток – с топливным двигателем его не будет, поскольку у него вращающий момент  сравнительно постоянен.

Модель испытывали на планирование в двух режимах: с закреплёнными жёстко крыльями и со свободными, подрессоренными аккумулятором крыльями (в естественном для этой модели положении). В последнем случае аэрокачество выше, в среднем, на 10%.

Фото 32. Махолёт «Алабино»

Фото 33. «Алабино» в машущем полёте, 2003 год.

Развитием модели «Алабино» стал мускульный орнитоптер «Азазель» (фото 34, 35). Его вес –45 кг, размах крыльев – 12 метров, площадь крыльев – 9 м², крылья как у «Джордано», но применена гибкая задняя кромка. Как уже отмечалось, они могут поворачиваться относительно продольной оси крыла, которая здесь конструктивно проходит по лонжерону крыла (22% от ширины крыла). Крылья также способны закручиваться упруго под действием внешних и внутренних сил. Но этого закручивания бывает недостаточно, например, когда жёсткость крыла велика.

Установили аккумуляторы, которые натягиваются при подъёме крыльев набегающим потоком воздуха и возвращают крыльям запасённую таким образом энергию при их опускании. Вес аккумуляторов небольшой – 240 граммов, они набраны из авиамодельной резины.

 Полная амплитуда махания - ±10^o . При начале разбега крыло машет внизу с неполной амплитудой ±5^o, затем, по мере роста скорости аппарата, амплитуда махания растёт, крылья поднимаются постепенно всё выше и выше.

В августе-сентябре прошлого года были проведены первые испытания на шоссейной дороге. Автомобили и, зачастую, боковой ветер затрудняли отработку аппарата. Удалось развить скорость 40 км/ч. Полного отрыва не произошло, но мы приблизились к нему. Переднее колесо отрывалась стабильно, а его расчетная скорость отрыва немногим меньше скорости отрыва основных колёс шасси.

Углом атаки крыла управлял специальный пружинный механизм. Затем я стал управлять рукой – стало лучше. Создавалось впечатление, что крылья нуждаются не столько в силе, сколько в правильном управлении.

Наряду с дождями начались сильные ветра, неугомонные и днём, и ночью. Мы укрепляли свои палаточные позиции. Когда дожди прекратились, стали испытывать изолированное крыло на ветру. Схема испытания, примерно, такая же, что и на рис. 5, но крыло здесь не вращалось по кругу – скоростной напор воздуха  создавался ветром.

 Я держал крыло в руках за корневую часть и управлял углами установки крыла ? -  оно  самомахало, то есть, приводилось в движение энергией теплоты  набегающего потока воздуха (см. также параграфы 2.8 и 2.9). При этом мы замеряли силу тяги крыла динамометром, соединённым с крылом десятиметровым резиновым шнуром. Резина усредняла силу тяги крыла – интегрировала её. При скорости ветра в 5-10 м/с тяга превосходила 2 кг, вечером, при безветрии, тяга составляла около 0,4 кг. На повороты крыла требовала незначительная мощность рук – не более 5 вт. Тяговая (полезная) мощность получалась около 150 вт и более. С ростом скорости ветра тяга росла значительно, так, что крыло резко уходило вперёд и по кругу, иногда заматывая резиновый шнур вокруг меня. Но после некоторого опыта от этого легко удавалось избавиться, направляя крыло вверх и немного назад.  И это видели проезжающие шофёры и гудели нам.

Два дня подряд, по три часа каждый день, делая небольшие перерывы, шестиметровое крыло махало, махало легко - как пёрышко.

Следующая задача – научиться махать двумя крыльями, управляя из кабины орнитоптера, сначала на ветру, затем – при движении аппарата по земле. На нашем крутом берегу Камы часто дуют сильные и стабильные ветра – они помогут нам.

Фото 34. мускульный орнитоптер «Азазель»

Фото 35.

 

2.13. О вертикальном взлёте махокрылов

Способы вертикального старта (без разбега) могут быть различны.

1 способ. Вертикальное положение корпуса и горизонтальное махание крыльев. Так взлетали наши модели «Искорка», «Встречная», «Гармония», «Петруша». Так зависают насекомые, птичка колибри и другие небольшие птицы.

2 способ. Корпус горизонтален, а крылья машут вертикально. Так взлетала модель «Алабино». У «Невидимки» при весе 7 кг на месте создавалась вертикальная подъёмная сила до 4 кг при больших установочных углах крыла b=30^o. У «Истины» эта сила доходила до 70 килограммов, у «Джордано» - до 18 кг, при нормальных углах установки.

Все махолёты отрывались от земли с меньшей скоростью, чем их планеры.

Наиболее эффективным может оказаться способ, занимающий промежуточное положение между 1 и 2 способом, как , например, при взлёте чайки или модели «Встречная».

3 способ. Крылья движутся по кругу (как у вертолётов) и машут. По этому способу взлетали модели-ротоптеры «Нимфа» и «Феофан», по этому способу действуют мускульные ротоптеры «Влади» и «Лузениана».

               

2.14. Размеры махокрыла  и экономичность полёта

Нам неоднократно приходилось увеличивать размеры какой- либо модели, выбранной за прототип будущего пилотируемого аппарата или большой модели. Стоит неверно задаться начальными условиями при проектировании, например, большим весом аппарата, так сразу получается парадоксальный вывод – большие махолёты летать не могут. И много можно допустить других ошибок.

Немало говорилось в литературе о том, что силы инерции станут проблемой больших машущих крыльев. Эту проблему связывают, во-первых, с потерей энергии  при торможении крыла и, во-вторых, с прочностью крыльев. Первая часть проблемы решена: одно крыло при торможении передаёт свою кинетическую энергию другим крыльям (посредством коленчатого вала или другого механизма), которые разгоняются. Этим принципом мы пользуемся с 1984 года, начиная с модели «РМ-4». На двукрылых  махолётах применяем упругие аккумуляторы и маховики. В полёте эта часть проблемы двухкрылок снижается либо исчезает (при  волнообразном полёте или при схеме «Джордано-3»).

Вторая часть проблемы (разрушающие нагрузки от сил инерции) решается в процессе проектирования с учётом всех факторов и экспериментов. При переходе от  модели «Встречная» к более тяжёлой «Невидимке» инерционные силы выросли в меньшей мере, чем  подъёмная сила. То есть, проблема  роста размеров махолёта не страшнее той, которая  существует в современной авиации с неподвижными крыльями.

При ударе крыла в нижнем его положении создаётся максимум подъёмной силы, который гасит силу инерции. В верхнем положении крыла сила инерции гасится частично весом крыла, а частично она дополняет подъёмную силу крыла, которая здесь слабее её среднего значения за период маха. Это относится к двукрылой схеме, хотя такой же режим можно организовать и на любой многокрылой схеме. Мы применяли этот метод на «Джордано», «Влади», «Лилиентале».

По нашему опыту, несущую способность летательного аппарата (вес аппарата, отнесённый к единице мощности двигателя) можно выразить формулой: @ , где G – вес аппарата, N – мощность двигателя, @ - знак пропорциональности, К – аэрокачество аппарата, К_дв – аэрокачество движителя аппарата (здесь – крыльев), V – скорость полёта..

При увеличении размеров аппарата  (в соответствии с законом квадрата – куба) в n раз, его скорость увеличится в  раз, К и К_дв  - тоже в раз. Следовательно,  вырастет в  раз. То есть, относительная доля мощности двигателя падает (падает и его доля веса в общем весе аппарата). При этом  (следует из расчётов) напряжения в материале лонжеронов крыла  от сил инерции не возрастают.

При увеличении размеров важно, чтобы не выходить за пределы закона квадрата-куба, то есть, чтобы вес рос не быстрее, чем в кубе. У летающих животных это выполняется вполне. У орлов, например, вес растёт пропорционально площади крыла. Современные самолёты с «упитанными» фюзеляжами в этом отношении просто порочны. Потому много «выпивают» и мочат нас сверху всякой нечистью, а крылу в живом воздухе поработать воли не дают.

Экономичность л.а. (см. параграф 2.3. ) можно выразить формулой: Е_уд =.

При увеличении размеров модели «Встречная» в 4 раза получилась модель «Невидимка», у которой шасси с колёсами давало дополнительное сопротивление. При этом получилось: =1,8, =2,2. Следовательно, =3,96. Опыты показали, что = 4,13.

При подобном увеличении размеров аппарата в n раз его экономичность улучшается тоже во столько же раз: . Удельные затраты на полёт снижаются в n раз. Это  рассуждение  по экономичности относится  к случаю стационарного изменения характеристик аппарата. При махании, как уже отмечалось, аэродинамика изменяется в лучшую сторону. Машущие крылья «Джордано» и «Азазель» дали силу тяги, практически, без подвода энергии.

2.15. Саморазгоняющийся планер

Крылья этих аппаратов дают тягу за счёт теплоты воздуха. Но следует иметь в виду, что эти крылья  при этом создают и подъёмную силу – крылья удерживали свой вес и вес добавочного груза. С ростом размеров аппарата его аэрокачество растёт, экономичность полёта – улучшается.

Всё это свидетельствует о целесообразности постройки и изучения планера больших размеров. Например, увеличить размеры крыла «Джордано» в 2 раза, затем оценить его сопротивление при разных скоростях и углах атаки, при различных состояниях атмосферы. Таким крыльям  можно дать свободу поворота относительно их продольных осей, как мы сделали на «Азазель». В этом случае можно создавать силу тяги в режиме колеблющегося крыла, а управлять планером по высоте   можно крыльями. У большого крыла эта тяга может достигнуть значений, достаточных для полёта. Привод колеблющегося крыла значительно проще привода машущего крыла.

Другой вариант – беспилотный. Можно сделать модель планера больших размеров (с размахом крыльев около 12 метров), уделив должное внимание форме крыла в плане. Наши крылья имеют профиль № 60, они давали тягу без махания (см. ранее), но не смогли преодолеть сопротивление фюзеляжа. У модели же фюзеляж значительно тоньше. Есть надежда, что такая модель планера сможет полететь без потери высоты. При необходимости этот планер можно преобразовать в орнитоптер.

Касаясь вопросов прочности, следует отметить, что у машущих крыльев флаттер теоретически невозможен, практически – не наблюдался.

 

Выводы по махокрылам

1.              Модели махолётов летают продолжительно, как у нас, так и за рубежом. Их полёт               более экономичен (даже на современной стадии их зарождения), чем полёт моделей с  воздушным винтом.

2.              Махолёты с человеком доведены до состояния отрыва от земли (у нас и в Канаде).

3.              Модели махолётов взлетают без разбега при небольшой мощности двигателя, на что неспособны модели самолётов с воздушными винтами.

4.              Произведён вертикальный отрыв аппарата с машущими крыльями за счёт мускульных усилий пилота (ротоптер «Влади»).

5.              С ростом размеров аппарата и скорости полёта удельные энергозатраты уменьшаются – машущий полёт становится существенно экономичнее. Воздушные винты самолётов в области околозвуковых скоростей испытывают значительные кризисные явления, конкурируя по экономичности с реактивными лайнерами. Кризис машущего крыла наступит  значительно позднее кризиса воздушного винта, поэтому и с этих позиций махолёты перспективнее.

6.              Созданы крылья, способные работать полностью за счёт тепловой энергии окружающего воздуха. Практически и теоретически обоснована реальность вечного двигателя, действующего за счёт энергии окружающей среды.

7.              Установлена способность любого крыла получать энергию из воздуха.

8.              Нестационарное  (неустановившееся) обтекание тел весьма выгодно отличается от установившегося обтекания, рассмотрением которого ограничивается современная академическая аэродинамика, за крайне редким исключением.

9.              На движение махолётов (как и на движение любых других тел в любом месте мирового пространства) оказывает влияние мировая  эфирная среда. Взаимодействие тел с этой средой рассмотрено во второй части данного трактата. Это взаимодействие может быть выгодным и достигать больших значений.

10.          Целесообразно всестороннее изучение аппаратов с машущими крыльями и аэродинамики нестационарных процессов.

 

Часть 2. Эфироиды

Глава 3. Взаимодействие эфира с материальными телами

3.1. Об эфире

Эфир – это материальная среда ,заполняющая всё мировое пространство, в том числе и то, в котором мы живём. Эфир – это реальный газ чрезвычайно мелкой структуры, частицы которого (амеры – по Демокриту) значительно удалены друг от друга в сравнении со своими размерами, подобно звёздам на небе. Все окружающие нас тела и вещества состоят из вихревых образований эфира.

Ещё работая над машущими крыльями, мы неуверенно обнаруживали присутствие какой-то среды, влияющей на работу крыльев, на их силу тяги.

Проводя опыты по осмыслению закона Бернулли, мне всё чаще думалось, что все известные силы в механике могут быть проявлением именно этого закона. Но для этого должна быть какая-то среда, тонкая материя, отличная от известных воздушных газов.

Вскоре мы познакомились с книгами Владимира Ацюковского, в которых современный учёный дал необыкновенно глубокий, всесторонний и логически здоровый теоретический анализ состояния всей современной физики и проблемы эфира, представив элементарные частицы, атомы, молекулы и вещество состоящими из вихревых образований эфира. При этом взаимодействия всех силовых полей успешно сводятся к взаимодействию подвижных газовых  вихрей эфира. Им определены ориентировочно многие параметры эфира (эфира -1) в околоземном пространстве. Например, давление  в эфире - 2·10³² н/м², плотность энергии  тоже огромна - 2·10³² дж/м³.

Принимаем, с учётом опыта предшественников, что эфир бесконечен внутрь, то есть амеры (амеры 1) состоят из вихревых потоков более мелких амеров (амеры 2), эти – из амеров 3 и т.д.. Пространство между амерами 1 заполнено амерами 2 (по аналогии с воздушными вихрями), пространство между амерами 2 заполнено амерами 3, и т.д.. Чем выше порядок эфира, тем больше его плотность, скорость, энергия. Получается, что все они стремятся к бесконечности. К тому же, невозможно представить себе неделимость какой-либо частицы, как невозможно при этом объяснить многие взаимодействия в природе.

Амеры 2 обладают очень большой плотностью, настолько большой, что средняя плотность эфирной среды 2 превосходит плотность любого металла во много раз. Обоснование большой плотности мы получили в результате анализа центробежной силы с позиций эфира (см. далее  параграф 3.3).

Это деление эфира может многое объяснить, снять противоречия при трактовке некоторых экспериментов, когда их пытаются объяснить с позиций только общего эфира, не вникая в его структуру. В действительности, одни амеры могут «отвечать» за оптику, другие – за гравитацию, третьи – за теплоту, электрические свойства и т.д. Как и в привычной для нас физике: в одном случае нам достаточно знать только плотность вещества, в другом случае приходится иметь дело с рассмотрением молекул, атомов и элементарных частиц.

Например, на воздушный шар действует две силы, обусловленные двумя различными  эфирными образованьями. С одной стороны -  это гравитация, вызванная разницей давлений эфирных амеров х по высоте, с другой стороны – это аэростатическая антигравитация, обусловленная высотной разницей давлений воздуха (сила Архимеда), который представляет собой эфирное образование на молекулярном уровне. Конечно, нам следует сейчас искать эфиростатическую антигравитацию (более сильную, чем аэростатическое воздействие), которая может быть обусловлена амерами y. В случае висения воздушного шара амеры гравитации и антигравитации отличаются, минимум, на 3  номера, то есть  у –  х  3.

Принимаем также, что каждое тело (шар, камень, планета, спутник, звезда…) имеет своё эфирное поле, изменяющееся по мере удаления от тела. При вращении тела его эфирное поле не вращается вместе с ним. Тщательного рассмотрения требует поведение эфира в пограничном слое Земли.

На позициях эфира стояли многие мыслители, начиная с самых  древних времён, в том числе: Анаксимандр, Аристотель, Декарт, Гюйгенс, Герц, Максвелл, Лаплас, Эйлер, Риман, Томсон, Энгельс, Циолковский, Миткевич.… Самым решительным образом против пустоты выступал Ломоносов. Философский труд Елены Блаватской «Тайная доктрина» наполнен множеством цитат учёных разных времён – цитат о необходимости признания эфира. В истории науки до 17 века труднее найти учёного , признающего пустоту, чем материалиста. Дошедшие до нас древние философские учения (Индия, Китай, Япония) и религии (за редким исключением) содержат в себе учение об эфирной среде (с различным её названием).

Ньютон тоже пришёл к признанию эфирной среды, но в конце своей жизни, когда его знаменитые «Математические начала…» уже «работали». Современная теоретическая механика академического мира по сей день базируется на пустоте, не считаясь с материальностью межпланетной среды.

Но и величайший авантюрист науки А.Эйнштейн (пытавшийся на пустоте из винегрета гипотез создать научную теорию) не смог обойтись без признания эфира. К сожалению, официальная наука об этом не знает (поскольку ей чаще приходится заниматься вопросами научного окружения, чем окружающей среды) и продолжает защищать начальные позиции законодателя науки, ссылаясь на эксперименты мистического характера.

Эти эксперименты не только неубедительны, но и анахроничны. К примеру, прогрессивные исследователи обнаружили скорости элементарных частиц, значительно превышающие скорость света. Но сторонники релятивизма утверждают, что это не скорость большая, а время – замедлилось:  V = .  Но заметим, что для обнаружения замедления времени необходимо счётчик времени поместить в систему координат, движущуюся со скоростью самой частицы (по той же теории относительности). А этого никто не делал.

Иногда меня спрашивают дети: «А что же находится между магнитами?». Прежде я отвечал, что ничего. И видел в лице первоклассника недоумение. Теперь отвечаю, что эфир. И замечаю улыбку.

В.А.Ацюковский в книге «Эфирный ветер» приводит историю и доказательства обнаружения эфирного ветра Морли, Миллером и Майкельсоном в начале прошлого века      ( с помощью интерферометра).

В 1996-98 годах сотрудник Харьковского НИИ радиофизики Ю.Галаев исследует и обнаруживает эфирный ветер в диапазоне радиоволн.

Судя по печати, всё большее число специалистов-физиков становится на позиции материальности межпланетной среды.

Мы проводили наблюдения по взаимодействию движущихся тел с эфирной средой. Это десятки механических установок, сотни экспериментов, тысячи замеров, анализ работы различных механизмов и систем, это астрономические наблюдения. В результате получены отклонения от законов классической механики, существенно превышающие погрешности наших измерений.

Под эфироидами  подразумеваем все тела и механизмы, взаимодействующие с эфирной средой и из эфира состоящие. Это в широком смысле слова. В частности будем иметь в виду такие объекты, взаимодействие которых с эфиром является определяющим или значительным.

 

3.2. Обнаружение эфирного ветра отвесом

В октябре 1997 года нами были проведены опыты по обнаружению эфирного ветра в шахте лифта многоэтажного здания, на высоте 160 метров над уровнем моря, на сравнительно возвышенной местности. Замерялись отклонения стального шара диаметром 90 мм, который был подвешен на тонкой стальной проволоке диаметром 0,3 мм и длиной 26 метров (рис.6). Замеры производились с помощью микроскопа с 60-кратным увеличением и специального измерительного устройства со шкалой, определяющего координату отклонения проволоки с шаром в направлении запад-восток с точностью до 0,01 мм. Нижняя часть шара помещалась в чашку с эпоксидной смолой, которая быстро гасит колебания и обладает высокой текучестью. 

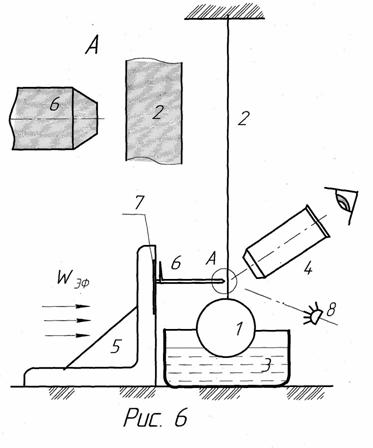
Отвес для обнаружения эфирного ветра.
1 – шар;
2 –проволока;
3 – чашка со смолой;
4 – микроскоп;
5 - измерительное устройство в сборе:
6 – винтовой указатель со стрелкой;
7 – шкала круглая;
8 – подсветка.

Наблюдения  в течение месяца показали разницу отклонений шара днём и ночью в 0,2 миллиметра. Это соответствует компоненте эфирного ветра, обусловленной орбитальным движением  Земли вокруг Солнца. Из этого опыта определяется сила действия эфирного ветра на шар:  F_эф = , где G – вес шара.

На большой высоте над уровнем моря, при отсутствии затенения фундаментом здания и рельефом местности эта сила может быть больше.

Этим способом можно оценить влияние материала, формы и размеров тел на силовое воздействие эфирного ветра.

 

 

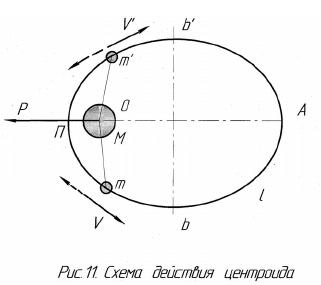
3.3. Центробежная сила с позиций эфира 

При движении любого тела по окружности возникает центробежная сила, направленная по радиусу от центра вращения. Эта сила пропорциональна квадрату скорости и обратно пропорциональна радиусу. Это установил ещё Гюйгенс.

Но какова природа этой силы -  что выталкивает тело из круга? Насколько точна формула Гюйгенса? Существует ли центростремительное ускорение?

При движении тела по окружности в воздухе на него действует дополнительная центробежная сила воздуха, в воде – центробежная сила воды, которая, примерно, в 800 раз больше, чем в воздухе. Это показали наши опыты с деревянными и пенопластовыми шашками, расположенными на вращающемся горизонтальном диске. Получается, что в более плотной среде больше и центробежная сила, причём, эта сила пропорциональна плотности.

Отсюда напрашивается предположение, что и центробежная сила Гюйгенса обусловлена эфирной средой, в которой движется тело. В таком случае плотность эфирной среды получается очень большой – она значительно (вероятно, на порядки) больше плотности любого металла. К такому выводу можно прийти, если учесть, что эфирная среда (в отличие от воздуха и воды) обтекает не всё тело, а лишь его непроницаемые амеры, объём которых  значительно меньше объёма всего тела. Наиболее ясно это видно из вывода формулы центробежной силы.

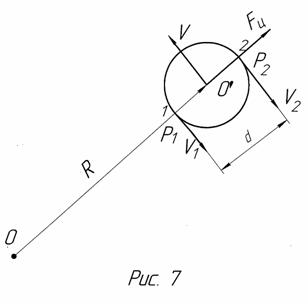
Получим формулу этой силы, исходя из того, что она создаётся разницей давлений эфира вокруг частиц-амеров движущегося тела. Пусть некоторый амер (имеющий диаметр d  и принадлежащий некоторому телу с массой m) с центром в точке О' (рис.7) движется по окружности радиуса R с центром в точке О со скоростью V. Пусть R >>d.

Из аэрогидродинамики известно, что выталкивающая сила F среды равна произведению объёма тела  v на градиент давления среды по направлению выталкивания :  F = v· gradР. Объём  амера будем считать постоянным. Рассмотрим, чему равен второй множитель.

Для точек амера 1 и 2, обтекаемых эфиром со скоростями V₁ и V₂, давления эфира будут соответственно Р₁ и Р_2. Разница давлений обусловлена разницей скоростей по закону Бернулли:

  gradР = =, где: - плотность эфирной среды, обтекающей амер о' ;   V₂ =V_{1  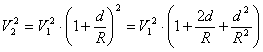;}  здесь третье слагаемое можно отбросить,

т.к. d <<R. Тогда  после подстановки, сокращения и замены V₁ на  V получим, что  gradР =. 

Следовательно, . .Получили выражение  выталкивающей или центробежной силы эфира, действующей на один амер движущегося тела. Для тела, содержащего n амеров, центробежная сила , где произведение   не является массой тела m , а является лишь величиной, пропорциональной этой массе: . Это произведение представляет собой массу эфирной среды, вытесненной амерами тела;  - коэффициент эфирной среды, зависящий от её плотности и давления. Получается, что масса вытесненной эфирной среды , примерно, равна массе тела. Учитывая, что вытесненный объём амеров меньше объёма тела, плотность среды получается больше плотности самого тела. Из рассмотрения движения шара, изготовленного из самого тяжёлого металла , получается, что плотность эфирной среды больше плотности самого тяжёлого металла. Это – как минимум. Но, вероятнее, что эта разница составляет порядки, как уже было отмечено в начале параграфа.

При движении в воде шара, плотность которого равна плотности воды, получается, что центробежная сила эфира, примерно, равна центробежной силе воды. Полная центробежная сила в 2 раза больше обычной центробежной силы, вычисленной по формуле Гюйгенса.

В наших опытах (движение медного тела в воздухе, влияние которого здесь можно пренебречь) получилось, что  > m , то есть реальная сила больше (на 5...10%) силы, рассчитанной по формуле Гюйгенса (). Это требует дальнейших проверок (в учебных заведениях демонстрируется лишь пропорциональность в формуле Гюйгенса , но не  равенство).        

Запишем окончательно формулу центробежной силы:

                   (3.3)

Таким образом, центробежная сила есть результат сквозного обтекания тела эфирной средой. Обтекаемые амеры тела (амеры 1) отличаются от амеров обтекающей среды

(амеров 2) размерами и порядковым числом.

Центробежная сила, как и по формуле Гюйгенса, пропорциональна массе тела, квадрату скорости и обратно пропорциональна радиусу движения тела.

Но в формуле Гюйгенса нельзя поставить знак равенства, поскольку центробежная сила зависит ещё и от плотности эфирной среды, в которой движется тело. Если эта среда неоднородна  по плотности, то и сила будет различной.

Знак равенства нельзя поставить ещё и потому, что объём амера v может, в принципе, изменяться под действием эфирной среды.

В связи с этим, интересным будет сравнение работы каких-либо центробежных приборов на Земле и вдали от неё, на дальней космической технике.

Центробежная сила не является следствием деформаций удерживающей нити, как учит нас академик Ландсберг. Наоборот – деформации и напряжения в нити являются следствием этой силы.

Центробежная сила не является силой инерции  (как преподносят нам в школах). Она является обычной силой, подобной силам аэрогидродинамики, как, например, подъёмная сила крыла. Причём, обе силы зависят от квадрата скорости движения. При равномерном движении  по окружности тело не имеет никаких ускорений (см. далее пар.3.4.2. и др.),            поэтому у него нет и силы инерции. Геометрические трактовки о центростремительном ускорении (на базе пустоты) оказываются неуместными, приводят к парадоксальным выводам при решении задач динамики полёта и других задач.

Особенно наглядно проявилась ошибочность в определении ускорений (как изменение вектора скорости за единицу времени) при решении задач по механике эфира. Под ускорением следует понимать изменение  только величины скорости. А направление имеет отношение только к геометрии.

К сожалению, векторная геометрия проникла во многие задачи теоретической и прикладной механики, часто уводя нас от истины, как и в случае задачи облёта планет. Авторы (76), пользуясь геометрическими приёмами, получают приращение скорости космическим аппаратом, например, при облёте Юпитера в 42 км/сек при орбитальной скорости этой планеты в 13 км/сек, что несовместимо с известными принципами механики.

К тому же,  векторная геометрия слабо развита. Например, неизвестно даже, как делить на вектор. А дифференцирование векторов уводит от физической сути, как было показано в предыдущих задачах.

Но обратимся к нашим дальнейшим задачам.

3.4. Движение тел под действием центральной силы

Сила, линия действия которой проходит всё время через одну и ту же точку, называется центральной. Например, движение планет вокруг Солнца происходит под действием центральной силы тяготения по линии Солнце-планета. Движение спутников Земли является тоже примером такого движения, если пренебречь влиянием других небесных тел.

Когда человек на вращающемся стуле (рис.10) притягивает гантели к центру вращения, то он увеличивает кинетическую энергию вращения тоже под действием центральных сил рук. В учебниках по механике здесь допускается ошибка, обусловленная чисто математическим подходом без связи с физической сутью явления.

 

3.4.1. Замечания о силе Кориолиса

Ошибка заключается в том, что применяется теорема Кориолиса, которая годится лишь для грубого описания случаев движения тела в «жёсткой» трубке. Эта трубка (или канал) движутся с постоянной угловой скоростью , что неприемлемо для свободного движения тела, когда угловая скорость изменяется, как и в данном случае со стулом.

Теорему Кориолиса ошибочно применяют при анализе отклонений падения тел на землю, например, в шахту. Опытные данные подгоняют под теорему, как и аналогичные задачи в учебниках.

Сила Кориолиса определяется по формуле(жирным шрифтом выделяем вектора): F_к = - a_к·m = -2 ωV_r ·m , где V_{r –} радиальная скорость движения тела массой m,  ω – его угловая скорость. Это в 2 раза больше, чем при свободном движении тела. Направления ускорения и силы Кариолиса противоположны.

При свободном же движении сила и ускорение имеют одно направление.

Применение теоремы Кариолиса для свободного движения (например, планеты) не соответствует закону сохранения энергии.

Ускорение у Кориолиса завышено в 2 раза ошибкой при взятии производной вектора переносной скорости, из-за отрыва от физики.

Сила Кориолиса (при движении в трубке) количественно верна, но не обоснована физически. Половина силы Кориолиса, действительно, является силой инерции: при приближении к центру вращения тело тормозится трубкой, при удалении – разгоняется. Другая же половина силы обусловлена действием центробежной силы, точнее, её проекцией на направление, перпендикулярное радиусу движения в плоскости орбиты (о ней будем говорить далее). Эта половина силы не даёт ускорения – не позволяет трубка. Сила Кориолиса – это сумма двух различных сил.

3.4.2. Свободное движение

На рис.8 тело массы m под действием центральной силы F  (с центром в точке О) движется по кривой L переменного радиуса  кривизны R' с центром кривизны О' со скоростью V. Точка П – перицентр орбиты L. Скорость тела, находящегося в точке в, разложим на 2 составляющие: V_R –радиальная, V_окр – перпендикулярно радиусу обиты R .

На тело m, помимо сил инерции, действуют 2 силы: центральная F (или центростремительная) и центробежная сила F_ц. Эту  последнюю силу нельзя отнести к силам инерции (см. предыдущий параграф 3.3)_.

В небесной механике считается, что планеты движутся под действием одной центральной силы, что окружное (азимутальное, трансверсальное) ускорение равно нулю (спис.лит.- 46), что планеты имеют только центростремительное ускорение (с.л.-59, 76), направленное всегда к центру тяготения по радиусу. Однако, вечно «ускоряясь», ни одна из них не приблизилась к Солнцу.

Что же это за алхиметрия?! Если планета не имеет окружного ускорения, то что же заставляет тогда её изменять окружную и угловую скорость, например, при переходе от апоцентра к перицентру?

Итак, центробежную силуF_ц , действующую по радиусу кривизны, разложим на 2 составляющие: F' – по радиусу орбиты (радиальная составляющая), F_окр – перпендикулярно этому радиусу – окружная составляющая.

С противоположной стороны от центра О в точке а движется центральное тяготеющее тело М (например, Земля, если m – Луна) с меньшим радиусом орбиты R_M = Оа.

На рис. 9 представлены ускорения, действующие на тело m. О них поговорим позднее.

Угол ψ – это угол между вектором орбитальной скорости V и вектором окружной скорости V_окр. Он положителен, если V_R – положительна. Угловая скорость ψ' положительна, если угол ψ растёт. При движении в  I четверти (как на рисунках) и в IV четверти центробежная составляющая F' по модулю больше центральной силы F на величину кс. Они равны при углах истинной аномалии θ= 90º и 270º, что следует из расчётов. Во II и III четвертях F'<F. За счёт разницы этих сил и возникает радиальное ускорение a_r , которое два раза меняет свой знак за 1 оборот тела по орбите. В I и  IV четвертях  это ускорение положительно – направлено от центра. Скорость положительна также при направлении от центра.

В I и II четвертях тело m , удаляется от центра О, окружная сила F_окр  направлена назад – тело тормозится (в окружном и орбитальном направлениях). В III и IV четвертях (движение от апоцентра к перицентру) -  ускоряется.

Эту окружную силу F_окр и заменяют в небесной механике и в ряде земных задач ошибочно силой Кориолиса.

 

 

 

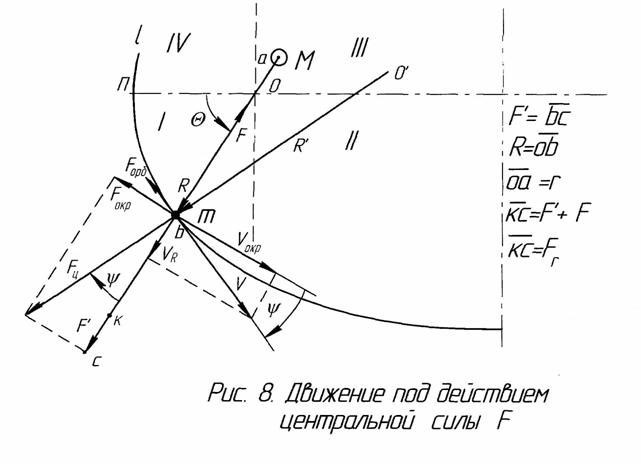
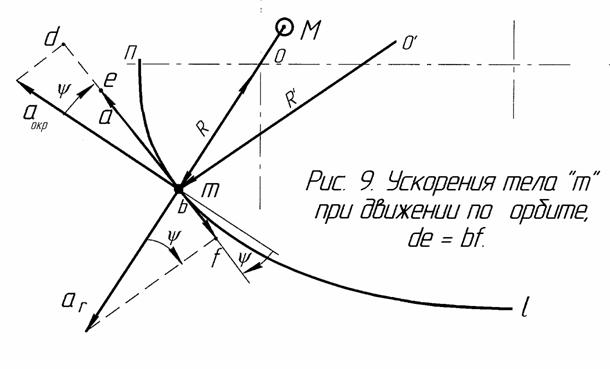
Определим величину окружной силы и окружного ускорения .

1 вариант вывода. Величина  этой силы была определена из сравнения работ центральной  и орбитальной сил. Производилось также сравнение работы орбитальной силы с изменением кинетической энергии тела m (например, для случая на рис.10) с учётом того, что при отсутствии момента внешних сил момент количества движения  постоянен (есть теорема), то есть в скалярном виде

L = m · V ·R·cosψ = const.

Задача решена на частных примерах и в квадратурах. Получилось, что все три энергии равны, если окружная сила (в скалярном виде) F_окр = a_окр· m = -V_R ·ω·m. Здесь: окружное ускорение a_окр= -V_R·ω ,  ω- угловая скорость. Знак минус (-) означает, что при положительной радиальной скорости V_R  (движение от перицентра к апоцентру - подъём) ускорение и сила отрицательны, то есть тело тормозится.

2 вариант. Величину окружной силы можно определить из 2 закона Кеплера, который запишем в скалярной форме:  Ś = ½ R V cos ψ = ½ R V_окр = const. Секториальная скорость Ś постоянна, поэтому её производная по времени равна нулю: Ś^'_t = ½ [ R'_t´V_окр+R·(V_окр)'_t ]= 0.

Здесь: R'_t =V_R -радиальная скорость, поскольку  R - скаляр;

( V_окр)'_t = a_окр- окружное ускорение; V_окр = ω·R_окр = θ'·R_окр .

Тогда уравнение можно записать так : 

V_R·ω·R_окр+R_окр·a_окр = 0 .  Сократив на R_окр, получим : a_окр = -V_R·ω.        ( формула 3.4.2.1)

Окружная сила, с учётом 2 закона динамики, будет равна:

F_окр = a_окр· m = - V_R·ω·m .               (форм.3.4.2.2)

Вновь получили такое же выражение окружного ускорения и окружной силы, что и в 1 варианте.

Ньютон, Лагранж и их последователи до наших дней допускают ошибку при выражении секториальной скорости Ś = ½ RV_окр . Её просто заменяют геометрическим выражением :

S = ½ , где радиус R_окр - фиксированная величина (в действительности R ≠ R_окр)  . При взятии производной это даёт другой результат – окружное ускорение  a_окр  получается с двойкой, как у Кориолиса, но с другим знаком.

3 вариант.  Вместо 2-го закона Кеплера (во втором варианте вывода) можно взять закон постоянства момента количества движения в скалярной форме: M = m V R cosψ. Результат опять будет таким же.

Таким образом, при орбитальном свободном движении тело имеет окружное (азимутальное) ускорение а_окр  под воздействием окружной силы эфира F_окр  = -V_R·ω·m.

Когда человек с гантелями вращается на стуле (рис.10), подтягивая их к себе, он ускоряется этой окружной силой. Этой силе приходится здесь разгонять не только гантели, но и человека со стулом. Поэтому ускорение разгона будет меньше, чем a_окр . Следовательно, в общем случае тело испытывает напряжённость окружной силы . А само ускорение тела будет a_окр = F_окр ׃ m_пр , где m_пр - приведённая масса тела (стандартное понятие).

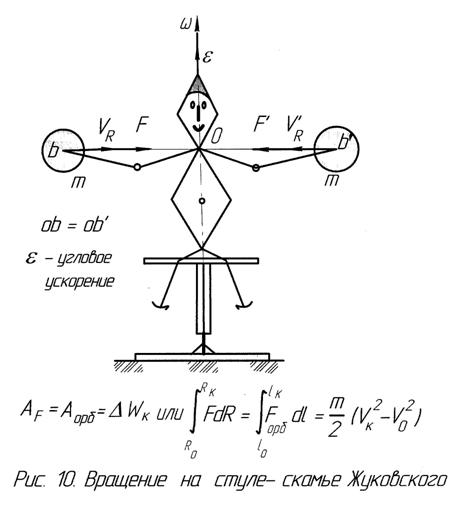
Определим связь между ускорениями свободного тела m ( согласно рис.8 и 9).

Продифференцируем по времени скорости :  V_окр = Vcosψ, V_R = Vsinψ. Получим значения окружного и радиального ускорений:

 а_{окр =}(V_окр)' =V'cosψ - V sinψ ·ψ' = a cοs ψ - Vψ'sinψ , где a =V' - орбитальное ускорение;

a_r =(V_R)' =V'sinψ+Vcosψ·ψ' = asinψ +Vψ'cosψ  - радиальное ускорение, направлено по радиусу орбиты; оно положительно, если направлено от центра.

После исключения произведения Vψ' из обоих выражений и несложных преобразований получим соотношение ускорений (в общем случае при несвободном движении - напряжений): 

a =a_окрcosψ +a_rsinψ                           (формула 3.4.2.3).

 

Орбитальное ускорение  равно сумме проекций окружного и радиального ускорения на направление касательной к траектории.

Орбитальная сила имеет направление ускорения и равна:  F_орб =ma            (3.4.2.4).

Для вычисления радиального ускорения  надо cумму центробежной составляющей и центральной (центростремительной) сил (с учётом их знака) разделить на массу тела:

a_r =                                              (3.4.2.5).

Здесь F_r  является радиальной силой, под действием которой и происходят радиальные перемещения и изменения скорости.

Умножим равенство 3.4.2.3 на массу тела m, получим: ma =ma_окрcosψ +ma_rsinψ.

Или, учитывая предыдущие соотношения и определения:

F_орб =F_окрcosψ +F_rsinψ                      (3.4.2.6).

Орбитальная сила равна сумме проекций окружной и радиальной сил на направление касательной к траектории.

Таковы реальные физические ускорения и силы, действующие на движущееся тело под действием центральной силы.

Заметим, что при определении ускорений производная бралась не от вектора скорости (как принято в классической механике), а от величины скорости. Как уже отмечалось в нашей работе (пар.3.3), ускорение – это изменение скалярной величины скорости (или просто – величины скорости). Направление ускорения определяется направлением ускоряющей силы.

Как видно, мы не обнаружили центростремительного ускорения и в данной задаче. Есть радиальное ускорение, которое может быть направлено как к центру, так и от центра. Оно соответствует реальным перемещениям и изменениям скоростей тела.

Нет центростремительных ускорений, есть центростремительные напряжения, вызванные центральной силой. И это следовало бы различать. Но физико-математики с этим не считаются. И складывают ускорения с напряжениями. И иногда получают теоремы.

Ускорение – это результат действия напряжений.

Следует обратить внимание, что окружные и орбитальные силы и ускорения дают проекцию на ось апсид (большая ось орбиты), всегда направленную к перицентру.

Справедливость полученных выражений можно проверить простым численным примером движения Земли вокруг Солнца.

Нами проводились различные эксперименты по вращению тел с переменным радиусом.

Под действием орбитальной силы эфира раскачиваются качели, падают тела, движутся планеты, спутники и т.д.. 

В литературе по баллистике и небесной механике в уравнениях орбитального движения, составленных в полярных или сферических координатах, присутствуют компоненты ускорения и силы Кориолиса, что даёт погрешность в расчётах траекторий.

Лишь то, что движется по Земле (поезда, реки…) или в «трубке» с постоянной угловой скоростью,  испытывает действие сил Кориолиса с учётом замечаний подпараграфа  3.4.1.

В случае свободного движения тела в поле центральной силы работает схема сил и ускорений, представленная в данном подпараграфе 3.4.2. По данной схеме раскачиваются качели, падают тела, движутся по орбитам спутники, планеты и т.д.. Маятник Фуко испытывает действие орбитальной силы, но оно не влияет на суточный период обращения плоскости качаний, поскольку действие этой силы за полупериод качания компенсируется её противоположным действием за следующий полупериод.

 

3.5. Эфирные движители – центроиды

3.5.1. Теоретическое обоснование 

Под движителем понимается механизм, с помощью которого можно отталкиваться от чего-либо и перемещаться в пространстве (колесо, гребной винт, машущее крыло и т.д.).

В данном случае будем говорить о механизме, с помощью которого можно отталкиваться от эфира (как на земле, так и в космосе).

Эфирные движители, основанные на концепции центральной силы, назовём центроидами. О них и будем сейчас говорить.

1 случай. При движении тела m по замкнутой орбите (рис.8, 11) относительно центра О, если он  неподвижен, суммарный импульс орбитальной силы F_орб (формулы в п. 3.4.2) даст силу   тяги P, которая направлена по оси апсид в сторону перицентра.

В самом деле, центральная сила (например, сила тяготения) между телом и центром даёт импульс. Но, как показал интегральный расчёт, её суммарный импульс равен нулю. Силы инерции, хотя и являются внешними, в механике не учитываются (их импульс также равен нулю). А вот центробежная сила – это внешняя сила, её импульс несбалансирован: у перицентра скорости движения больше, чем у апоцентра. Скорости определяют импульс центробежной  силы в проекции на ось апсид АП .

Был проведён интегральный расчёт импульса  центробежной силы при движении тела m.  При движении тела по левой половине эллиптической орбиты b'Пb (рис.11) этот импульс существенно больше, чем при движении по правой половине bAb' (полуорбита апоцентра).

Силу тяги можно вычислить по формуле:

Р =                   (3.5.1).

Здесь: =, -половина приращения скорости при движении от апоцентра к перицентру,  R_a ,R_п –радиусы апоцентра и перицентра орбиты, ε – эксцентриситет орбиты.

Силу тяги можно вычислить и по другой формуле: Р =       (3.5.2).

Здесь:   - осреднённое (среднее интегральное) по времени окружное ускорение.

Всё это справедливо в случае неподвижного центра тяготения О, вокруг которого движется тело m.

2 случай. В общем случае относительно неподвижного центра О движется и центральное тяготеющее тело большой массы М (рис.8 и 9) с малым радиусом орбиты r = oa. Таким примером является система Земля+Луна. Оба тела движутся  вокруг их общего центра масс, который находится от центра Земли на расстоянии r = 4670 км. Тело М  также испытывает действие орбитальной силы, величина которой точно равна величине орбитальной силы малого тела m (спутника), но направление сил – противоположно.  Суммарный импульс этих двух сил равен нулю – тяги Р нет.

3 случай. Если запустить второй такой же спутник m' , но в противоположном направлении, симметрично относительно линии апсид орбиты (рис.11), то тело М окажется в центре О, способном двигаться  взад-вперёд  вдоль линии апсид при движении спутников.

 

В этом случае тело М не испытывает действие центробежной силы. Оно движется  теперь под действием только центральных сил (силы тяготения  тел m' и m). Но суммарный импульс центральных внутренних сил системы m+m'+M  равен нулю (как и в случае 1). Из всех сил, определяющих движение центра масс системы, остаются две центробежные силы тел m и m'. Их импульс даёт тягу в сторону перицентра, которую приближённо можно определить по формуле 3.5.1 или 3.5.2.

Направление движения спутников не имеет значения – главное, чтобы они двигались в противофазе.

Второй способ обоснования силы тяги центроида  для 3 случая  заключается в раздельном рассмотрении тела M и спутников m, m'.  Тело M испытывает действие только центральной силы. Как показал расчёт (для кеплеровской орбиты), общий импульс этой силы за период обращения  в проекции на ось апсид равен нулю.

Спутники испытывают действие центральной и центробежной сил. Импульс центральных сил в проекции на ось апсид равен нулю (из расчёта интегрированием). А импульс центробежных сил опять не равен нулю.

Таким образом, центробежная сила спутников определяет тягу Р центроида.

 

Образный пример. Когда шарик скатывается по наклонной плоской поверхности с небольшим уклоном под действием силы притяжения, он получает горизонтальный импульс движения (количество движения), который значительно больше импульса движения (количества движения) в направлении действия силы притяжения.

Роль наклонной плоскости в центроиде выполняет эфир посредством центробежной силы.

 

Для работоспособности движителя-центроида необходимо выполнение условия: центральная сила между телами-спутниками m, m' и центральным телом (корпусом движителя) должна изменяться по закону: F =, где n – показатель степени, n>0, то есть сила должна возрастать с уменьшением радиуса орбиты.

Следовательно, движение грузов-спутников на обычных пружинах не даст силы тяги. Можно применить комбинации пружин, магнитные устройства, мускульный привод и другие решения.

При движении планет и спутников (при кеплеровском движении) это условие выполняется в связи с действием закона тяготения. Центроиды-спутники могут найти применение в космосе для перемещения различных небесных тел (планет, комет, астероидов, спутников, различных искусственных и естественных космических систем).

3.5.2. Опытное обоснование центроида

Самым распространённым движителем такого типа является сам человек. Мы много раз проводили опыты на плоту, как в клубном бассейне, так и в лесном – в глухом заросшем ущелье тихими вечерами (рис.12).

 

В  случае 1 (вид сбоку) руки с грузами m и m' движутся в вертикальной плоскости, как при беге. В случае 2 руки движутся в горизонтальной плоскости. В обоих случаях грузы движутся с переменным радиусом относительно плеч человека, в противофазе, как и спутники на рис.11. Была получена сила тяги от 2 до 8 граммов, плот массой 280 кг заметно перемещался.

Подобные опыты целесообразно было бы провести в космосе, предварительно потренировавшись  на земле в закрытом бассейне. Распределение скоростей грузов и мышечных усилий, а также форма траектории грузов имеют большое значение.  Космонавт может преодолеть первый метр разгонного пути за 1 ... 2 минуты (при нулевой начальной скорости). Можно сделать наоборот: вначале слегка оттолкнуться от стенки корабля, затем затормозиться силой тяги центроида. При наличии тяги центроида космонавт может возвратиться к исходной стенке.

Движение ног при беге аналогично движению рук  в вертикальной плоскости (с точки зрения о центральной силе) – они также должны давать силу тяги. Мы провели такие опыты при езде на велосипеде без педалей и получили положительный результат в 90 опытах из 100 проведённых. На чистоту опытов влияло трение и движение воздуха. Подобные опыты можно также провести в космосе.

Следующим примером центроида являются качели.

Если качающийся маятник m  (рис.13)  подтягивать за нитку тогда, когда он идет влево, и опускать – когда он идет вправо, то среднее положение шарика отклонится влево – вверх. Это свидетельствует о наличии импульса орбитальной силы, которая в проекции на горизонталь создает силу тяги  Р.

У качели с человеком телом m является человек, который с помощью ног и рук изменяет радиус R. Центральной силой здесь является сила ног и рук. Чтобы раскачать качель, надо вставать в нижней точке и приседать в верхней; для торможения -  все делать наоборот. Это замечание следует учитывать для того, чтобы получить силу тяги при незатухающих качаниях.

Мы успешно проводили опыты по нарушению равновесия большого рычага с помощью орбитальной силы, являющейся следствием центральной и центробежной сил (рис. 14 ).

Нами проводились опыты по получению силы тяги и движения  качели на бревне по кругу  вокруг  вертикальной оси, закреплённой на пне дерева (фото 36, 37). Получена сила тяги в 300 граммов. Для лучшей эффективности и наглядности необходимы: большая жёсткость узлов  вертикального шарнира и строго вертикальное расположение оси этого шарнира.

Политехнический музей Москвы представил на первый всемирный интеллектуальный фестиваль качель на колёсах (фото 38), которая двигалась рывками, но довольно быстро.

Рис. 14

Фото 36. Качель на длинном бревне

Фото 37. Двойная качель (после урагана)

Фото 38

Фото 39. Эфирный движитель «Шарманка» в протоке р. Камы.

Фото 40. Движитель «Радж» сдвоенный.

Фото 41. Эфироид «Крестовый» состоит из 4 движителей.

 

Гимнасты при выполнении упражнения «солнышко», курсанты лётных училищ при вращении на лопинге (металлическая качель с вращением в вертикальной плоскости относительно горизонтальной оси) используют окружную силу эфира. Если лопинг или перекладину гимнаста укрепить на тележке – она покатится, подобно качели из музея или нашей лесной качели с круговым движением.

Для уменьшения тряски и вибраций движители можно сдваивать или счетверять, синхронизируя их работу в противофазе (фото 39 - 42).

Фото 42. Испытания движителя «Толчин». Слева – Артём Ложкин, справа – Владимир Крылов. Над изготовлением установки активно работал Слава Белоногов.

 

3.6. Инерция и инерцоиды-движители

Было предпринято много попыток создать инерцоид – движитель, действующий за счёт сил инерции. Однако их теоретическая суть не имела убедительной физической основы – они должны были отталкиваться от пустоты, «данной» нам Ньютоном. Но опыт энтузиастов имеет здесь большое значение, ибо даёт информацию для создания теории таких движителей.

С нашей точки зрения, физическая суть инерцоида заключается в изменении инертной массы тела под действием эфира в зависимости от кинематических параметров движения (скорость, ускорение и его производные: скорость ускорения, ускорение ускорения и т.д.).

Скорость движения  влияет на сопротивление эфира (см.опыт по эфирному ветру 3.2). Это демонстрирует отклонение от 2 закона динамики. Принципиально, это позволяет создание эфирных движителей малой тяги – инерцоидов.

Ускорения a не изменяют существенно инертную массу m_ин , если они малы и постоянны в процессе разгона или торможения. А если они велики, если изменяются при этом , то что же будет с массой в этом случае? Ньютон и Лагранж «согласно природе дифференциального исчисления» и геометрических методов обобщили 2 закон динамики на все случаи. Но физика не подчиняется математике. Математика является всего лишь инструментом для познания физики. А потому следует обратиться к эксперименту.

Скорость движения – это первая производная пути по времени, ускорение – вторая производная, скорость изменения ускорения назовём третьей производной. Существует четвёртая, пятая, шестая производные и так до бесконечности. Все они, если не равны нулю, могут оказывать какое-то влияние на массу и движение тела посредством эфира. Сила инерции – это результат сложного взаимодействия частиц-амеров движущегося эфирного тела с частицами-амерами эфирной среды.

Примером изменения инертной массы является выстрел из автомата Калашникова АКМ. Пуля массой 7,9 грамма приобретает скорость 715 м/сек за счёт сгорания 1,6 граммов пороха. Кинетическая энергия пули при выходе из ствола равна 2020 джоулей. Расчёты показывают, что пуля для разгона получает только около 500 джоулей. Остальная энергия газов уходит на нагрев ствольной части автомата, преодоление трения пули в канале ствола, разгон самих газов, работу подвижных механизмов. Часть энергии теряется от недорасширения  газов из-за того, что ствол в десятки раз короче, чем требуется для полного расширения. Получается, что инертная масса пули меньше массы покоя, примерно, в 4 раза.

Наблюдается существенное влияние скорости движения тела на его инертную массу (помимо влияния на сопротивление эфира). В автомате (как показали наши стендовые испытания в войсковой части 3479) импульс отдачи, примерно, равен импульсу пули с газами. То есть, относительная инертная масса автомата, примерно, такая же, что и у пули, хотя у них разные ускорения. Дело в том, что у них разные и скорости. Ускорения уменьшают инертную массу, а скорости увеличивают её, примерно, в той же пропорции.

У тяжёлого физического маятника (рис.15) с ростом его длины L скорость растёт (при равных угловых амплитудах φ) – растёт и инертная масса, в связи с чем период качаний увеличивается (по сравнению с расчётным, расчёт периода колебаний производился по уравнению нелинейных колебаний с применением компьютера). Это сравнение наиболее наглядно при наибольших амплитудах (60º÷90º) когда скорости и ускорения наибольшие) и при большой длине маятника (>2,5 метров). Влияние аэросопротивления  учтено дополнительными опытами с подобными, но лёгкими маятниками из дерева и пенопласта.

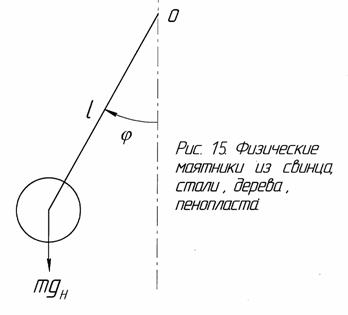
У большого тяжёлого маятника изменение периода колебаний с ростом амплитуды было меньше, чем у маленького (из того же металла). Производились аналогичные сравнения с маятниками из пористого материала (пенопласта). Эти сравнения, наряду с другими, наводят на мысль о влиянии размеров тела на его инертную  массу.

Влияние размеров крыла  на его присоединённую массу воздуха наблюдалось нами в экспериментах по аэродинамике. Удивительное влияние размеров шара на период колебаний наблюдалось в экспериментах по гидродинамике (с маятниками).

Влияние скорости на инертную массу наблюдается при качании очень длинных маятников с относительно небольшой амплитудой, когда ускорения малы и их влияние значительно меньше влияния скорости. Для читателя таким примером могут явиться маятники Фуко.

В Петербурге, в Исаакиевском соборе, в 1931 году был установлен маятник длиной 98 метров с периодом качаний 19,8 сек при амплитуде ±5 метров (к большому сожалению, сейчас этот замечательный маятник снят, но хранится в архивах музея собора). Расчёт периода качаний этого маятника с учётом массы подвесного троса (около 10 кг) и массы самого маятника (54 кг) по формуле для физического маятника (известной из курса средней школы) даёт значение периода в 19,5 секунд. Это несовпадение периодов на 1,5 % соответствует увеличению инертной массы на 3 %.

В Париже, в здании Пантеона, установлен маятник длиной 67 метров, массой 28 кг, с периодом качаний 16,4 секунды. Здесь также наблюдается увеличение периода качаний (и массы маятника) по сравнению с расчётным значением. Нас очень интересует значение периода качаний этого маятника при малых амплитудах ( меньше ±0,3 метра) и толщина подвесной проволоки. Просим тех, кто будет в Париже! сделать такие наблюдения и сообщить нам. Будем благодарны за любые уточнения по этим и другим маятникам, установленным в других городах.

Следует иметь в виду, что на период качаний влияет сопротивление движению маятника ( во всех наших опытах он от этого уменьшался) и толщина подвесной проволоки ( с тонкой проволокой период был меньше в связи с ростом упругих деформаций). Оба эти влияния растут при увеличении амплитуды качаний маятника.

Влияние скорости на инертную массу  проявляется также и при падении шаров с разных высот. Например,  с высоты 96,6 м стальной шар диаметром 90мм падал с ускорением g =9,4 м/сек² (сопротивление воздуха 2% уже учтено). С высоты 1,5 м ускорение шара было 10,2 м/сек². С высоты 0,3 метра – 10,3÷10,5 м/сек². И лишь с высоты 15÷20 метров шар падал с классическим ускорением 9,8 м/сек². Наблюдается уменьшение ускорения свободного падения с ростом высоты.

Следует отметить, что при падении происходит также изменение силы тяготения Земли, о чём будет рассказано далее.

Сопротивление воздуха уточнялось  опытами с различными шарами при падении с разных высот. Например, 4 шара ¢ 90 мм разной массы сбрасывались поочерёдно (с фиксацией времени падения) и попарно (для определения разницы высот  падения за одно и то же время). Использовалась видеотехника.

Влияние 2-й и вышестоящих производных на инертную массу прослеживается при пусках стальных шариков стартёром из резины или пружины. При разгоне шарика вверх он поднимается выше, чем следует из расчёта по энергии, полученной от стартёра.

Мы уменьшили третью производную путём механической обработки резины (предварительной вытяжкой). Это увеличило кинетическую энергию шара на 11% при той же энергии старта.

Следует также обратить внимание, что динамическая жёсткость стартёра  отличается (в ту или другую сторону) от его статической жёсткости, определяемой при тарировке пружины. Динамическую жёсткость можно определить в режиме  колебаний маятника по периоду колебаний (вертикальных или горизонтальных).  Это различие «жёсткости», определяемое по периоду, свидетельствует об изменении инертной массы маятника при его движении.

Если запустить вверх шарик резиновым стартёром длиной , то получим высоту подъёма h. Если стартёр сложить пополам, увеличив ускорения разгона (и прочие производные) в 2 раза (при прежней энергии стартёра), то высота подъёма шарика увеличивается, иногда, на десятки процентов. Это обусловлено меньшей инертной массой во втором случае.

В этих опытах необходимо бывает учитывать внутренние потери в стартёре, особенно,  в резиновом. Их можно учитывать по затуханию вертикальных колебаний в маятниковом режиме. В каждом случае эти потери различны.

При движении Земли и Луны наблюдаются изменения орбитальной скорости в связи с неравенством инертной массы и массы покоя (см. далее в 4 главе).

Если сбросить шар с высоты и резко (a_торм≈ 25g) затормозить его стартёром, то работа торможения получается на  ~50% меньше энергии падения, ввиду уменьшения инертной массы шара  при торможении по сравнению с инертной массой при ускорении падения. Здесь отличаются ускорения (и прочие производные) при равенстве средних скоростей разгона и торможения.

Когда человек прыгает с большим ускорением, то он «облегчается» (см. рис.16, фото 43, 44). Это «облегчение», в основном, связано с уменьшением инертной массы человека в момент толчка о тележку. Импульс действия сил на тележку фиксируется  динамометром через длинный резиновый жгут. При измерениях в лесу этот жгут мы довели до 50 метров, что позволило получить продвижение тележки вперёд (при прыжках) на 25 сантиметров. Это соответствовало среднему уменьшению «веса» человека на 8%. Различные факторы трения учитывались и сводились к минимуму.

Рис. 16.

Фото 43. В покое

Фото 44. При прыжках

Производились также горизонтальные пуски шариков стартёром, пуски под углами ±45º. Артём Ложкин изготовил  катапульту «Кенгуру» (фото 45). С её помощью исследовалась баллистика и динамика полёта свинцовых шариков массой 70 граммов при пуске под углами от 0 до 90º. Нами наблюдалась работа различных механических систем в неподвижной и в подвижной системах координат.

В результате анализа большого количества экспериментов рождается вывод об изменении инертной массы, об её неравенстве с массой покоя, об отличии этих двух взаимосвязанных понятий.

Масса покоя – это мера количества вещества. Инертная масса – это мера физического взаимодействия тела с окружающей средой.

Если присоединённая масса эфира при ускорении тела мала, то мала будет и инертная масса этого тела.

Количественно эти массы могут быть как больше массы покоя, так и меньше.

Фото 45. Катапульта «Кенгуру» и два бомбардира – Павел и Иван.

Изменения массы, однако, ещё недостаточно для получения работоспособного инерцоида, поскольку импульсы сил двух взаимодействующих тел всё же равны (пока равны, но необходимы дополнительные точные замеры), поскольку относительное изменение массы получается у них одинаковым.

И мы сделали инерцоид из системы 3 тел, подвижных друг относительно друга (рис.16). Штанга подвешена на вертикальной нити. На ближнем конце штанги закреплено массивное тело Ред (редуктор модели махолёта), к нему на винтах крепится авиамодельный двигатель меньшей массы Д, внутри двигателя ходит поршень П. Выхлопные газы двигателя идут вниз. При работе двигателя  силы тяги нет.

Но, когда винты крепления двигателя ослабили (появился люфт – двигатель стал подвижен относительно тела Ред), то появилась  тяга P силой 10 граммов (влево, в сторону двигателя). При зажиме двигателя тяга опять исчезала.                        

Исходя из результатов опыта,  можно предполагать, что в случае системы трёх тел происходит неодинаковое относительное изменение массы этих тел.

Следуя этой идее, мы сделали инерцоид «Картезий» (фото 46, рис.17), состоящий из нескольких подвижных тел. Электрический двигатель m₂  подвешен на штанге m₁ через стальную рессору. Штанга может вращаться на вертикальной оси. На оси двигателя закреплён лепесток, на котором размещены грузики m₃  и m₄ на разных расстояниях от этой оси.

Фото 46. Инерцоид «Картезий», двигатель с грузиками – на левом конце штанги, напряжение питания – 12 вольт.

 

При работе штанга вращалась сколько угодно долго, набирала скорость и после отключения электрического тока вращалась ещё несколько кругов по инерции. Движение штанги – безостановочное, то есть, трение в подшипнике вертикальной оси всё время направлено против движения и никаким образом не может создавать импульс тяги.

Сопротивление воздуха тоже не может создавать тяги, так как наибольшая скорость лепестка (внизу) направлена против движения штанги.

Движения тел весьма своеобразны. Штанга, например, может совершать только вертикальные движения, тяга движителя при этом максимальна и равнялась 18 граммам.

Размещение грузов m₃ и m₄  на лепестке, их величина и соотношение играют большую роль и могут менять направление силы тяги на противоположное.

Затем мы привязывали двигатель прямо к штанге (к этой и к другой, более длинной и гибкой) без рессоры. Штанга опять могла ходить вверх-вниз и нисколько не ходила вправо-влево (при вращении лепестка), совершенно не подчиняясь ни теореме о движении центра масс, ни закону сохранения импульса. При этом была получена сила тяги  и скорость движения конца штанги до 2 м/сек (с более длинной штангой) как в горизонтальной, так и в вертикальной плоскостях. Двигатель вращался с частотой около 20 герц. В каждом эксперименте частота требовалась определённая, соответствующая распределению грузов на лепестке и на штанге.

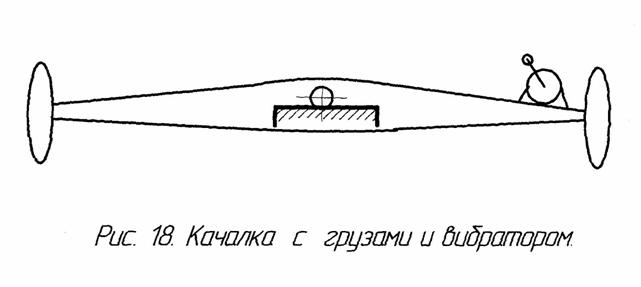
Проводились различные опыты с маятниковыми качалками (рис.18). На штанге около одного из двух грузов устанавливался электромоторчик на 4 вольта (он работал от батарейки) от детской игрушки. На оси моторчика укреплялся лепесток с эксцентричным грузиком массой 3 грамма. При вибрациях от этого двигателя вся система массой в 160 кг качалась в вертикальной плоскости с разгоном или без затухания. Трение, воздух и автоколебания здесь не имеют влияния.

При других, более гибких, штангах с более мощным вибратором (электролобзиком), амплитуда  увеличивалась на 15 сантиметров за одно колебание штанги.

Таким образом, подтверждается предположение, что в случае сложных колеблющихся систем изменяется не только инертная масса, но и суммарный импульс системы. Это позволяет создание эфирных движителей – инерцоидов.

Закон сохранения импульса системы нарушается, как и в случае с центральной силой.

Были изготовлены и исследованы мускульные инерцоиды «Радж» (фото 47) и «Радж-2». Тяга «Раджа» на земле (пол, асфальт) составила при последних измерениях 1,6 килограмма (по динамометру, по ускорениям разгона )  при сопротивлении трения колёс в 1,7 кг. Для аналогичного разгона посторонней тягой требовалась сила 3,3 кг. При движении с горки получали безостановочное движение, при этом создавали как переднюю, так и заднюю тягу около 1 килограмма. На воде (на плоту) тяга была меньше – 0,4 кг. Целесообразно инерцоиду дать свободный ход-люфт «взад-вперёд» при установке его на плоту, например, ставить его на колёса, закрепив сзади резиновым шнурком.

Тяга «Раджа-2» (фото 40) была несущественной, здесь почти отсутствовало движение самого корпуса инерцоида и 2 человек, если грузы (правые и левые) двигались со смещением фаз на полпериода. При отсутствии смещения фаз этот сдвоенный движитель принципиально не отличается от «Раджа» и развивает тягу, в 2 раза большую, чем «Радж».

Фото 47. Испытания инерцоида «Радж» на асфальте и на воде.

Фото 48. Эфироид «Немо». Испытывался с резиновыми и электрическим двигателями, в герметичном кожухе и без него, на воде и на подвесах, с различным положением конструкции в пространстве. Опыты с ним существенно дополнили информацию об ускорениях и об эфире.

 

3.7. Инерционные  эфирные двигатели

Под эфирным двигателем  мы подразумеваем механическую систему, способную получать энергию из эфирных полей и изменять своё кинетическое состояние за счёт этой энергии. Безусловно, мы говорим пока о принципиальных двигателях, а не о промышленных образцах.

В данном случае речь идёт о телах, способных получать энергию за счёт изменения инертной массы. Изменение массы обусловлено разницей ускорений при разгоне и торможении. Большему ускорению соответствует меньшая инертная масса. Инертную массу m в зависимости от ускорения a можно приближённо оценить формулой:

(3.7.1).

Здесь: m_o –масса покоя, k₂ – коэффициент пропорциональности (отрицателен), n₂ –показатель степени.

Аналогичная формула для влияния скорости на массу,  (см. также 3.8.1) : 

(3.7.2).

Коэффициент k₁ > 0.  Но в данном случае (с двигателем)  средние скорости разгона и торможения равны и не дают разницы импульсов.

Эксперимент 1. В 1999 году испытывался двигатель «Новогодний» (фото 49). Вертикальный диск диаметром 1 метр жёстко закреплён на горизонтальном валу. На этот же вал жёстко насажен и фигурный кулачок. Вал с диском вращаются относительно вертикальной оси (в центре круглого стола) и относительно своей горизонтальной оси, то есть диск, опираясь на кулачок, может катиться по кругу. За счёт профиля кулачка движение происходит с ускорениями и торможениями. При прямом движении величина ускорения разгона больше ускорения торможения. За счёт разного изменения инертной массы диск получает несбалансированный попутный импульс сил инерции (при прямом движении), при обратном движении – тормозной импульс.

Из сравнения этих двух движений была определена разница положительной и отрицательной работ эфира по перемещению диска, была определена разница инертных масс за счёт разницы ускорений.

В данном эксперименте разница была очень мала и сравнима с погрешностью опытов. Но это была ценная информация о влиянии малых ускорений на массу, необходимая при общей оценке.

Эксперимент 2. Этот же дюралюминиевый диск, утяжелённый стальным кольцом, испытывался на другой установке «Инерция» (рис.19) в неподвижных подшипниковых опорах. Фигурный кулачок 1 имел выступы и впадины. При вращении диска кулачок (жёстко соединён с диском) «обкатывался» роликом 2, который прижимался грузом 3 (или пружиной) посредством рычага 4.

Ускорения диска в этом эксперименте были в 10÷20 раз больше, что позволило получить существенную разницу положительной и отрицательной работ эфира. Диск тормозился, но с разницей (при прямом и обратном вращении) в 1,26 раза.

Производилось также сравнение работы установки с круглым и фигурными кулачками.

Во всех опытах наблюдалось влияние диаметра ролика и формы профиля кулачков на движение. Эти параметры влияли на распределение ускорений, на их непостоянство, то есть на третью производную пути по времени (t) =(t), которая может изменять инертную массу.

При больших скоростях диска сказывается эффект проскакивания ролика, вертикальные силы инерции проявляют существенное действие, снижая основной эффект  обоих экспериментов.

Эксперимент 3.  Эти опыты проводились в середине 90-х годов. Но ещё раньше подобные сравнения проводились на дисках диаметром 0,5 метра (в горизонтальной и вертикальной плоскостях), которые дали ещё большую разницу (в 1,5 раза) в затухании прямого и обратного движения (установка «Кеплер»).

Фото 49 Эфирный двигатель «Новогодний» (принципиальная установка), 2000 год.

Рис. 19. Эфирный двигатель «Инерция».

 

3.8. Разгон диска падающим грузом

Проводились опыты по разгону диска на оси в подшипниковых опорах (рис.20) падающими грузами (в различных комбинациях весов и высот падения). Работа деформаций нитей подвески (из стекловолокна) учитывалась.

Эксперимент 1. О влиянии ускорений на инертную массу. Диск разгонялся (по расчёту) в двух случаях  до равной  кинетической энергии системы «диск + груз» при равных ускорениях грузов, но при разных ускорениях диска (а_{1 =}2а_{2 ,} индекс 1 присвоен опыту с малым радиусом). Для этого требуется выполнение условий опыта: G₁ =4G₂ , H₁ =0,25H₂  , G₂·H₂ =G₁H₁ . Под ускорением диска понимается касательное ускорение точек окружности инерции с радиусом , где: J – момент инерции диска, m – масса диска.

При разнице расчётных ускорений диска Δa =3,28 м/сек² (a₁ =6,56 м/сек²) получилась (после разгона) разница кинетических энергий системы «диск + груз» на 7%. Эта разница обусловлена 3 факторами: 1) – разница ускорений диска, большему ускорению соответствует меньшая инертная масса, 2) разные скорости груза влияют на инертную массу груза, большей скорости соответствует большая масса, 3) разные скорости груза влияют на их притяжение к Земле, но разница скоростей и её влияние здесь сравнительно малы.

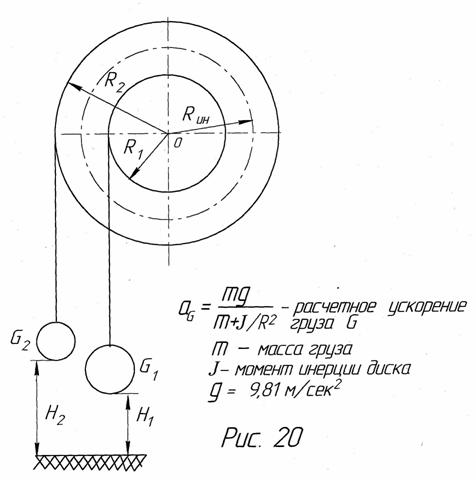
Эксперимент 2.  О влиянии скорости на массу и тяготение. Груз G₁ падал с разных высот H (больших, чем в предыдущем эксперименте) с расчётным ускорением  4,55 м/сек².

При увеличении высоты в 4 раза (расчётная скорость падения увеличилась в 2 раза) ускорения груза и диска уменьшились в 1,088 раза, при увеличении высоты только в 2 раза (скорости – в 1,41 раза) ускорение уменьшилось в 1,041 раза. Здесь проявилось изменение тяготения груза и изменение массы груза и диска.

Эксперимент 3. О влиянии скоростей и ускорений грузов на их массу и тяготение. Для проведения сравнения двух опытов были выполнены условия: G₁=2G₂ , H₁=0,5H₂ .

Здесь изменяется масса грузов и притяжение их к Земле, причём, это происходит и за счёт ускорений , и за счёт скоростей, результаты зависели и от соотношения массы грузов к массе диска.

В случае с лёгким грузом (большие ускорения и скорости груза) получено меньшее ускорение диска.

Эти опыты, наряду с прочими, в данной работе отмеченными и не отмеченными, позволяют приближённо судить о физической картине изменения  инерции и тяготения.

В данных опытах третья производная равна нулю (ибо ускорения постоянны). Для большего представления о её влиянии следует проводить опыты, когда она постоянна (четвёртая производная равна нулю).

Изменение инертной массы можно представить общей формулой (см. также 3.7):

 

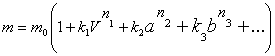(3.8.1)

Здесь коэффициенты пропорциональности k_i  и показатели степени n_i следует определять и уточнять опытным путём, методом последовательных приближений. Эта формула позволяет надеяться на  получение различных эффективных эфирных механизмов. Эта формула не запрещает создание инерцоида

При сравнительно небольших  скоростях (меньше 50 м/сек) и ускорениях (меньше 50 g), когда ускорения постоянны, у поверхности Земли, на основании ограниченного числа опытов и наблюдений, в международной системе измерений СИ (м, кг, сек), ориентировочно можно полагать:                                

(3.8.2)

Эта частная формула позволяет создание инерционного (или массового) эфирного двигателя (3.7).

Требуется увеличение числа различных опытов и их обработка.

 

3.9. Свободное падение тел и гравитация

О свободном падении шара с различных высот уже говорилось  в параграфе об инерцоидах (3.6.). При падении тел происходит не только  изменение инертной массы, но и отклонение от закона всемирного тяготения.

Вывод этого закона, приводимый в учебниках, является приближённым и незавершённым.

Во-первых, в основу вывода положена замена притяжения однородного сферического слоя притяжением точечной массы. Нами были просчитаны эти соотношения для тела на поверхности сферы с применением компьютера (Юрий Белый и Андрей Топоров) и двойных интегралов. Оказалась разница в 3,14 раза – сфера притягивает сильнее точки. Внутренние сферы шара дают  всё меньшую разницу. Неравномерное распределение плотности Земли (она растёт по мере приближения к центру Земли) также уменьшают эту разницу. Но! Она значительна.

Эта разница проявилась при оценке гравитационной константы, когда расстояние между опытными массами было сравнительно мало (спис. лит.-73).

Во-вторых, константа «тяготения» может меняться в зависимости от кинематических параметров движения тел V, a, b, ... , как и в случае с инертной массой.

Рассмотрим падение шара диаметром 90 мм с малых высот H (2-й опыт 2-й серии), зафиксированное видеокамерой (Владимир Крылов) с интервалом между кадрами в 0,04 секунды (рис.21 с таблицей 3).

В таблице указаны текущие ускорения  (значения ΔΔΗ необходимо умножить на коэффициент расстояния 0,967, обусловленный разницей расстояний от видеокамеры до шара и до шкалы). В последнем столбце указано среднее ускорение падения.

Получилось волнообразное изменение параметров падения. Текущие ускорения изменяются от 7,86 м/сек²  до 12,69 м/сек² (см. рис.21а «Падение шара»). Отсчёт времени - от положения шара при H=50 мм

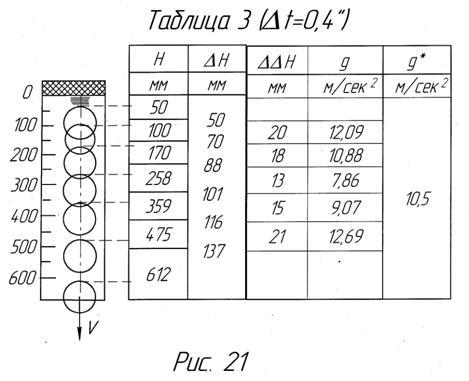
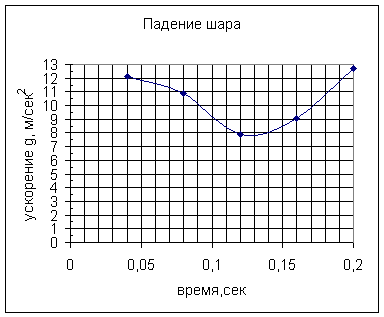
Рис. 21а.

Если рассмотреть падение шара с интервалом между кадрами в 0,02 секунды (с большей частотой видеосъёмки), то наблюдаемые ускорения падения (таблица 4) изменяются в ещё большем диапазоне: от  –82,5 м/сек² до 102 м/сек².

Таблица 4

Как видим, ускорения изменяются в большом диапазоне, наблюдается кратковременная антигравитация с восьмикратной перегрузкой. И это не объяснить только ростом погрешностей – они могли увеличиться лишь в 8 раз по сравнению с предыдущим опытом, в то время как разница ускорений изменилась в 38 раз.

Видеотехника тарировалась по работе большого физического маятника (перед опытами и после них) – её точность была достаточной. Видеоизображения подвергались обработке с помощью компьютера.

Ускорение свободного падения g зависит от напряжённости гравитационного поля g_{н .} Напряжённость обусловлена разницей давлений эфира по высоте – градиентом давления эфира grad P_эф. Используя положение аэрогидродинамики о выталкивающей силе среды (F), которая здесь направлена к центру Земли, по аналогии с выводом центробежной силы (3.3), можно записать: mg_н=F =v·grad P_эф . Отсюда выразим напряжённость:            

(3.9.1).

Здесь:  v –эфирный объём тела, равный объёму амеров гравитации,  ρ – эфирная плотность тела.

Если оценить средние ускорения падения шара (по 4 опытам) и учесть изменение его инертной массы  при падении по формуле 3.8.2, то получается, что при малых скоростях падения (H≈0.3м) напряжённость поля тяготения имеет наименьшее значение ~10,4м/сек².

Но при малых скоростях движения маятника результаты будут иными – ближе к  классическим, поскольку другими будут ускорения движения.

При падении напряжённость поля растёт с ростом скоростей и ускорений:                      Δg_н /ΔV≈ 0,055 1/сек , Δg_н/Δa ≈ 0,06. Эти значения градиентов напряжённости поля (по скорости и по ускорению, соответственно) носят, конечно, ориентировочный характер.

Таким образом, динамическая напряжённость гравитационного поля  отличается от статической. Это изменение может происходить, например, за счёт изменения объёма амеров тела или градиента давления эфира.

Явления пульсаций параметров движения наблюдались во многих опытах по вращению различных дисков в вертикальной плоскости, например, при их торможении сопротивлением воздуха и трением в подшипниках. Такие пульсации обнаруживались даже обычным секундомером. Наблюдаются волны с длиной периода в десятки секунд и более.

При уменьшении интервала измерений растёт амплитуда колебаний ускорений диска. Графики торможения имеют при этом волнообразно-игольчатый характер (рис.22, по вертикальной оси – изменение кинетической энергии диска за 1 оборот). При горизонтальных пусках   этого не наблюдалось.

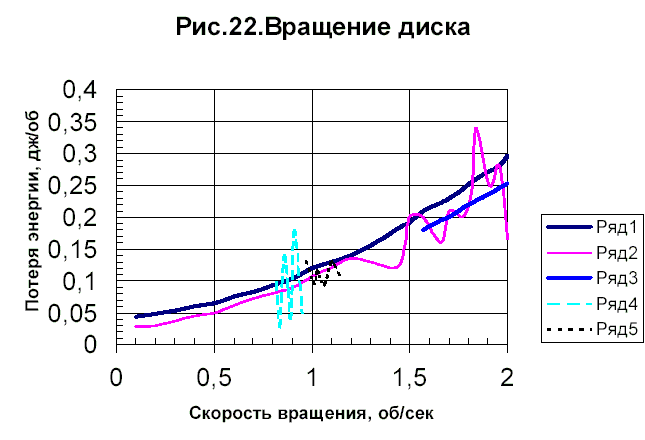
В ряду 1 представлена раскрутка горизонтального диска (диаметром 1 метр, массой 50 кг) график имеет сравнительно ровный, монотонный характер. Остальные ряды – это графики вращения того же диска в вертикальной плоскости. Ряд 2 –график с тем же интервалом замера, что и ряд 1. Ряд 3 – большой интервал замера, ряд 5 – меньший интервал, ряд 4 – самый малый интервал замера (60 сек.). Целесообразно провести опыты при меньших интервалах замера скорости с применением видеотехники.

Диски делались, исходя из известных требований для уменьшения сопротивления и некоторые могли вращаться от разгона рукой около суток.

Похоже, что при всяком движении тела в вертикальной плоскости оно подвергается дополнительному влиянию гравитационного поля, по сравнению с влиянием при покое или при горизонтальном движении.

Это влияние представляет собой силовое взаимодействие  тела и эфира, оно имеет волнообразный характер с различными гармониками. Гармонике с низкой частотой соответствует меньшая амплитуда.

В следующем параграфе  будет представлена схема гравитационного взаимодействия диска с эфиром.

 

3.10.Гравитационные двигатели

Если на вертикальном вращающемся диске (рис.23) выделить какую-то частицу массы m, то эта частица за 1 оборот будет испытывать разные отклонения силы тяготения ΔF от своего нормального значения F_о=m_оg_но=m_о·9,81м/сек². Здесь g_но – коэффициент напряжённости поля тяготения у покоящегося тела. При вращении F =F_о+ΔF =mg_н . 

Схема А может измениться и превратиться в схему В при некотором сочетании производных V, a, b, …, о которых говорилось ранее. Схема А соответствует разгонному импульсу эфира, схема В – тормозному.

Рассмотрим схему А.

При движении точечного тела m от точки 1 к точке 3 оно будет тормозиться  за счёт изменения тяготения ΔF, при движении от точки 3 к точке 1 оно будет разгоняться. Эти импульсы неравные, поскольку нижние отклонения ΔF больше верхних за счёт больших градиентов давления . Градиенты связаны с напряжённостью поля тяготения (см. 3.9.1).

Таким образом, за полный оборот каждая точка диска получит положительный разгонный импульс эфира.

Разница сил тяготения по высоте (разница градиентов давления эфира) приближённо  обоснована законом  всемирного тяготения. Мы уточняли эту разницу, например, с помощью двухметрового маятника. Были произведены замеры тяготения на глубине 840 метров в шахте им. Ленина в г. Кизел (1996 год) и на вершине горы Косьвинский камень (Уральские горы) на высоте 1500 метров. Измеряли земное притяжение на заводских трубах и высоких зданиях. У поверхности Земли наблюдается изменение  тяготения, в десятки раз превышающее табличные значения справочников. Иначе говоря, при приближении к поверхности Земли разница градиентов давления эфира растёт и эта разница имеет существенное значение.

Кроме нас, в шахту с этой целью опускались австралийцы, которые тоже обнаружили отклонения в значении гравитационной константы на глубине (Сп. лит. - 73).

Если тело m на лёгком диске является дисбалансом (ось о является неподвижной), то скорость этого тела в точке 1 будет больше средней скорости, а скорость в точке 3 – меньше средней скорости вращения.

Аналогичную разницу скоростей можно получить (и она была получена) при вращении несимметричной, но сбалансированной штанги с грузами (рис.24).

Здесь малый груз m имеет большие ускорения (влияние других производных здесь менее значительно, например, скорости были малы сравнительно с ускорениями)– соответственно его тяготение к Земле изменялось в большей относительной мере, чем у большого груза М. Поэтому в большей мере изменялся и момент вращения малого груза. Из-за разницы моментов скорость штанги менялась. В точке 1 скорость малого груза была на 8% больше, чем в точке 3.

При изменении размеров штанги и скорости вращения соотношения скоростей в точках 1 и 3 меняются. Штанга демонстрирует волнообразную реакцию эфира на кинематику движения (производные пути по времени).

Целесообразно проводить большее число опытов с применением видеотехники. Следует учитывать затухание при движении, прогибы штанги и т.д.. Всё это решается.

По схеме А получают энергию из эфира различные наши установки.

Качалки (фото 50) диаметром до 5 метров с двумя свинцовыми грузами на концах (до 76 кг каждый) качались по несколько суток от толчка рукой. Сопротивление движению с грузами  получено меньше, чем без грузов (при равных скоростях и ускорениях штанги – то есть при равных периодах качаний штанги и штанги с грузами). При малых амплитудах (2мм) наблюдалось безостановочное движение качалки с грузами - без затухания (при горизонтальном положении ).

Вертикальный свинцовый маятник (фото 52 ) массой 12 кг иногда «на глазах» увеличивал амплитуду своих качаний на 12÷15 сантиметров. Но это не было стабильным явлением, поскольку в этих системах работа эфира соизмерима с работой сил сопротивления (воздуха и трения), зависящих от атмосферных условий.

Однако, работа эфира была стабильной. Это обнаруживалось путём сравнения тяжёлых маятников с подобными, но более легкими, которые отличались по массе в десятки раз. Этот метод сравнения мы применяли при анализе работы различных движущихся систем.

Испытывались диски. На фото 51   представлена установка «Михайло». Диск весом 300 кг и диаметром 1 метр заключён в герметичный кожух. После раскрутки диска стартёром (через заклеиваемое окошечко) кожух заполнялся гелием, который обладает значительно меньшей вязкостью, чем воздух. После этого диск при скорости 3 об/сек вращался с таким малым затуханием, что его полное «сопротивление» (замеренное по потере кинетической энергии) было меньше сопротивления в подшипнике. Эфир помогал вращению диска.

В другом опыте этот же диск, но без кожуха, мог вращаться сколько угодно долго при скорости около 0,5 об/сек, если трение в подшипнике искусственно создавалось нулевым.

Сравнивались тяжёлые и лёгкие диски при постоянных и равных скоростях вращения. На  вращение тяжёлых дисков требовалась меньшая мощность двигателя – при выборочных скоростях. Наблюдалась и обратная разница – при других скоростях вращения. При разгоне тяжёлых дисков применялся отдельный стартёр, сравнение проводилось с помощью маломощного чувствительного двигателя.

Исследовалась работа дисков диаметром от 0,125 м до 1 метра. С ростом диаметра общее удельное сопротивление вращению сильно падает (см. далее).

Поэтому целесообразно изготовить диск большего диаметра (2метра и более), весом до 100 кг,  жёсткой конструкции (для снижения пластических деформаций). Он сможет вращаться без кожуха и гелия и при обычных  качественных подшипниках.

Это будет вечный эфирный двигатель (гравитационный), каким являются планеты и спутники, преодолевающие сопротивление самого эфира, космической пыли, газов, различных излучений и возмущений от других небесных тел.

По этому гравитационному принципу, подобно частице m диска, планеты получают энергию эфира как для вращательного движения вокруг своих осей, так и для орбитального – вокруг центра масс Солнечной системы. В обоих случаях есть вертикальные перемещения частиц планеты относительно центра тяготения – Солнца.

Спутники планет получают энергию аналогично. Но у них 2 центра тяготения – Солнце и своя планета. При вертикальном  перемещении относительно Солнца они получают энергию для орбитального движения вокруг Солнца, при вертикальном перемещении относительно планеты они получают энергию для движения по орбите вокруг планеты.

Испытывалось вращение штанги с грузами на концах, конструкция которой подобна качалке на фото 50. Сравнивалось их движение в вертикальной и горизонтальной плоскостях. Получена работа эфира (в вертикальной плоскости) в 420 граммо-сантиметров (0,041 джоуля) за 1 оборот на 1 килограмм грузов при скоростях вращения –0,5 об/сек. Радиус вращения грузов – 1 метр. У штанги потеря энергии на пластические деформации больше, чем у дисков. Воздушное сопротивление дисков меньше. Поэтому диски в этом смысле предпочтительнее. Но требуется тщательная оценка взаимодействия с эфиром. Скорости и ускорения имеют важное влияние.

Аналогичные сравнения производились и с дисками различных размеров и массы           (до 300 кг). На рисунке 22 (пар.3.9) уже был представлен график, из которого можно оценить работу эфира у вертикального диска. Сопротивление подшипников отличалось несущественно и оно падало с ростом скорости вращения (оценка трения проводилась при  невращающихся  дисках, а ось вращалась). Радиус инерции диска меньше, чем у штанги, примерно, в 3 раза. Это значительно уменьшило удельную работу эфира у диска.

С ростом размеров диска в 2 раза  его масса увеличивается в 8 раз, разница градиентов давления эфира по высоте растёт, примерно, в 2 раза, путь частиц диска растёт в 2 раза. Поэтому работа эфира всего диска должна увеличиться в 32 раза. Некоторые опыты свидетельствуют о более крутой зависимости. Требуются уточнения.

Работа воздушного сопротивления увеличилась в 4,7 раза при увеличении диаметра от 0,5 метра до 1 метра. Работа трения в подшипнике выросла в 16 раз, но она составляла меньшую долю в общем сопротивлении, особенно, при большой скорости вращения.

Сравнивалась работа жёстких качалок  с грузами (фото 50; рис.18, но без вибратора) при горизонтальном положении (грузы двигались вертикально) и при вертикальном (грузы двигались горизонтально). В первом случае получалось более медленное затухание (иногда в несколько раз) колебаний, а период колебаний был меньше (при больших амплитудах  - до 4,5 %) при равных дисбалансах.

Испытывался специальный блочный маятник (рис.25) при различных амплитудах (до 29 метров) движения грузов. Удельные потери энергии (на 1 оборот шкива) получались меньше при больших амплитудах, хотя сопротивление движению росло пропорционально квадрату скорости. При небольших амплитудах опытные ускорения превышали расчётные.  Предположительно, такой маятник после отработки сможет работать без затухания.

Все эти и другие опыты свидетельствуют о возможности получения энергии гравитации. Следует иметь в виду, что любое тело способно не только получать, но и отдавать свою энергию эфиру. Отдача энергии в эфирное поле является полезным механизмом регулирования  природных процессов, например, скорости движения небесных тел.

Возможно, это понадобится для регулирования теплового баланса на Земле.

Фото 50. Качалка с грузами

Фото 51. Диск вращается в кожухе с гелиевой средой

Фото 52. Свинцовые маятники

 

3.11.Эфир и махокрылы

Всё более очевидной становится связь машущего полёта с эфирными полями. Чем больше частота махания, тем более сильные изменения веса и массы махокрыла происходят при его движении.

Не потому ли летает жук, что использует эти поля при  своих вибрациях? Не потому ли миллионы стрекоз летели пульсациями в сторону грозы (часть 1)? В пульсирующем режиме летают почти все мелкие птицы – то опускаясь, то поднимаясь (подобно частице диска).

Но главное – все летающие животные машут, получая энергию из эфирных полей, изменяя свой вес, создавая нужный импульс сил инерции, связанный с изменением массы своего тела. Присутствуют другие эфирные эффекты.

Эти факторы, в целом, наиболее эффективны, если: ускорения крыла вверху меньше, чем внизу, а движение вверх, примерно, симметрично относительно вертикали. Движение крыла подобно движению баскетбольного мяча при ударах о пол, падению шарика в наших различных опытах с вертикальными пусками (с торможением и разгоном пружиной или резиной) или прыжкам человека на тележке, где наблюдалось изменение вертикальных импульсов сил.

Такое движение наиболее эффективно и с точки зрения  аэродинамики (хотя бы потому, что сильный вихрь внизу увеличивает горизонтальную скорость при подъёме крыла, что необходимо для выравнивания подъёмной силы – для уменьшения чрезмерных  вертикальных колебаний корпуса  в случае двукрылой  схемы).

При машущем полёте не только крылья, но и сам  корпус махокрыла совершает  умеренные вертикальные колебания (у двукрылой схемы), подобные по характеру колебаниям крыльев. Это подобие обусловлено опять же работой мощного нижнего вихря. Это увеличивает подъёмную силу махокрыла    за счёт благоприятного изменения инертной массы крыльев и  корпуса.

Горизонтальные пульсации махокрыла за счёт нижнего вихря, аналогично вертикальным, создают горизонтальный импульс сил инерции – это увеличивает тягу.

Но вибрируют ещё и перья птицы и создают не только аэродинамическую, но и эфирную тягу, как создаёт её вибрирующий лепесток на  инерцоиде «Картезий».

В соответствии с движением воздушного потока вдоль крыла  (рис.26 и рис.5а) и в связи со сказанным в параграфе 3.4.2,  на поток воздуха вдоль  машущего крыла (присоединённая масса крыла) будет действовать окружная сила эфира F_окр (по формулам 3.4.2.2 и 3.5.1 или 3.5.2). Эта сила  через воздух воздействует и на крыло. Эта сила может эффективно проявить себя при взлёте с места при больших углах атаки (по 2 способу).

При махании (у птиц) консольная часть крыла то приближается к корпусу (при подъёме крыла), то удаляется (при опускании). Такое движение массы консоли вместе с присоединённой массой воздуха также создаёт окружную силу эфира, направленную вверх,  в плоскости махания.

Присоединённый вихрь крыла при опускании крыла является эфирным роторным движителем (см. в следующей главе 4), его тяга направлена вперёд – по направлению полёта. При движении крыла вверх этот эффект менее значителен.

Таким образом, на махолёт действует несколько эфирных факторов, повышающих его подъёмную силу, тягу и экономичность.

В случае симметричного синусоидального движения крыла (как на «Джордано», «Элоне», «Истине»…) работает меньшее число эфирных факторов: получение энергии из эфира, причём, только посредством крыльев, поскольку корпус махолёта вертикально неподвижен; роторная тяга сохраняется; подъёмная сила от окружной силы существует. Инерционные факторы выражены слабее из-за меньших пульсаций.

 

Глава 4. Движение небесных тел  под действием эфира

4.1. Общие вопросы

4.1.1. О сопротивлении эфиром.

Таким  образом, все небесные тела получают энергию из гравитационных эфирных полей (обусловленных центральными тяготеющими телами) для поддержания своего движения, которое тормозится тем же эфиром и газопылевыми структурами космоса (не путать с торможением по схеме В, пар.3.10). Влияние тормозного действия можно объяснить, например, опытом по обнаружению эфирного ветра (3.2).

С ростом размеров тела сопротивление эфира на единицу массы тела должно падать, поскольку передние частицы тела снижают скорость эфирного потока, действующего на последующие частицы (если эфир давит на тело, то и тело давит на эфир).

В таком случае, тяжёлый спутник должен испытывать меньшее удельное сопротивление эфира, а лёгкий – большее. Вот почему Луна движется без замедления, а искусственные спутники падают на Землю.

Можно запустить небольшой спутник на орбиту, близкую к лунной и сравнить движение спутника и Луны. Во-первых, можно будет оценить сопротивление встречного эфирного ветра, обусловленного орбитальным движением вокруг Земли. Во- вторых, из-за влияния солнечного эфирного ветра (от движения вокруг Солнца) скорость спутника в точке 1 (1четверть по астрон. классификации, см. также рис.27) будет больше, чем в точке 3 лунно-спутниковой орбиты. Эта разница составит, минимум, 40 м/сек, если верен наш опыт по обнаружению солнечной компоненты эфирного ветра. У Луны такой разницы не обнаруживается, что может свидетельствовать о малом удельном сопротивлении эфиром ввиду её больших размеров и массы.

Эфир испытывает существенное изменение своей скорости (относительно Луны) лобовыми слоями лунного грунта, которые экранируют последующие слои. В этом случае работа гравитационного поля справляется с работой сил сопротивления.

Таким образом, движение спутника должно иметь два отличия от движения Луны: замедление и пульсация скорости по орбите.

 

4.1.2. О влиянии эксцентриситета орбиты

Чем больше эксцентриситет орбиты ε, тем больше радиальные ускорения, тем большему воздействию гравитационного поля подвержен спутник (или планета) – либо торможению, либо разгону (параграф 3.10).

Целесообразно было бы сравнить поведение двух космических спутников равной конструкции, но с различным эксцентриситетом орбиты. Трудность сравнения может возникнуть из-за разницы скоростей и высот орбит. Но полезна и приближённая оценка, особенно, не одного, а нескольких сравнений. На большем удалении от Земли влияние атмосферы меньше, поэтому и сравнение будет более правильным.

Земля и Луна движутся по эллипсам  и получают энергию по схеме А. При движении по окружности нет прибыли энергии из эфира – планета потеряла бы скорость и стала падать.

Вот почему небесные тела движутся по эллипсам – ответ на вопрос Эдмунда Галлея  Ньютону: «Исаак, но почему планеты движутся по эллипсам?».

 

4.1.3. О гравитационной константе

Произведение гравитационной константы G  (входящей в закон всемирного тяготения) на массу центрального тела M называется планетоцентрической константой. Вычислим эту константу применительно к движению Луны вокруг Земли, то есть, определим геоцентрическую  константу, исходя из 3-го закона Кеплера:

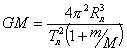.                  (4.1.3.1)

Здесь: R_л – большая полуось лунной орбиты, T_л  - период обращения Луны вокруг Земли,  m/M – отношение массы Луны к массе Земли.

Воспользуемся данными Астрономического ежегодника за 2002 год (октябрь-ноябрь). Получим:  GM =3,90876·10¹⁴ м³/сек² = 0,98062(GM)_ст. Как видим, в данном сравнении получается значение на 2% меньше стандартного значения, принятого в небесной механике и в астрономии (GM=GE=3,986005·10¹⁴ м³/сек²). То есть, нет совпадения с лабораторными замерами. Этого следовало ожидать, исходя из сказанного ранее в параграфе 3.9 (при близком расстоянии сфера притягивает сильнее, чем точка)

Можно, конечно, просто списать такое расхождение солнечным возмущением лунной орбиты, как это и делается в  учебниках. Но не является ли такое решение опрометчивым и голословным? Для более убедительного ответа следует оценить влияние возмущений на  гравитационную константу. То есть, сделаем ещё один ход, не зависимый от первых, но подтверждающий отклонение  «постоянной» тяготения от её классического значения и от её абсолютного постоянства. Под константой (постоянной) тяготения будем подразумевать её среднее значение.

Полагая пока массу Земли такой, какой она определена, заметим, что и постоянная тяготения G меньше стандартного значения на 2 % .

Весьма важным является вопрос – какова гравитационная константа на поверхности Луны? Ведь её можно было определить хотя бы с помощью пружинного динамометра или маятника, даже не выходя из лунного отсека. Причём, сделать эти замеры следовало в первую очередь и  немедленно доложить на Землю. О данных экспериментах нет никакой информации (есть информация о лунно-орбитальных гравитационных замерах). Похоже, что они не проводились. И здесь уместно слово американских астронавтов и учёных-гравиметристов.

Нет никаких данных и о гравиметрических замерах на поверхности Луны  советскими и американскими лунниками.  Какова гравитация на поверхности Венеры, Марса…? 

 

4.2. Возмущающее действие эфира на движение Луны

Будем рассматривать возмущения (отклонения, неравенства) параметров орбитального движения Луны (скорость, радиус орбиты…) от кеплеровского движения. При этом нас интересует физическая сторона вопроса, качественный и количественный характер изменений скорости движения. Всё это с той целью, чтобы получить математические соотношения, более ясно согласующиеся с физической моделью движения, отработать их, а затем производить более точные расчеты, как в небесных, так и в земных задачах механики.

Например, при наших наблюдениях за Луной отклонения от данных астрономических календарей (или ежегодников) доходили до 2 минут по времени и более. При этом эти отклонения после анализа и различных сравнений укладывались в рамки той физической концепции, которую предлагаем.

1-е возмущение . Гравитационное от Земли. Луна при движении по своей орбите вокруг Земли (рис.27) то приближается к ней, то удаляется, как точка m на диске (схема А  на рис.23). Точка 4 соответствует перигею, точка 2 – апогею лунной орбиты. Разница движений Луны и точки m диска только внешняя: точки диска движутся в стороне от Земли, а Луна – вокруг Земли. Принципиальных же отличий в данном случае нет. Луна, как и точки диска, получает энергию за счёт гравитационного эфирного поля Земли. Под воздействием  этого переменного поля происходит периодическое изменение орбитальной скорости Луны.

 В точках 1 и 3 (точки смены знака радиальных ускорений относительно Земли в соответствии с рис. 9 и парагр. 3.4.2) наблюдаются приращения (изменения по величине) скорости Луны:       ΔV=V₁-V¹ ≈ V²-V₂ ≈ 0,0184V_ср , где V¹ и V² являются расчётными скоростями кеплеровской орбиты с учётом других известных возмущений. Скорость подъёма V₁ больше скорости опускания V₂ (как и у несимметричных  качалок и штанг,  рис. 24).

Это соответствует отклонению лунно-земных суток T_л от их расчётного значения T_л^* на ±1 минуту по времени (± 1'). Лунно-Земные сутки – это интервал времени между двумя последовательными прохождениями небесного меридиана через диск Луны (определение автора, по аналогии с солнечно- земными сутками). Расчётное значение суток  соответствует движению Луны по кеплеровской орбите с учётом других известных возмущений.

Приращение скорости ΔV и относительное приращение скорости ΔV_отн  определялось из соотношения: ΔV_отн== ,                        (4.2.1.)

 где Т_зв=23º 56' 3,5"=23º56,058' – звёздные сутки, Т_л определяется из наблюдений,
=24º 50,52' - средние лунно-земные сутки.

Для отмеченного изменения скорости необходимо среднее изменение напряжённости поля (исходя из закона сохранения энергии) Δg_н=±0,34g_н , которое определялось по формуле:

;                                        ( 4.2.2.)

ΔR – изменение радиуса орбиты за четверть периода, g_н -  средняя напряжённость поля тяготения для данной орбиты.

2 и 3 возмущение. Подобный эффект Луна испытывает и за счёт гравитационного поля Солнца. Но он слабее, минимум, в 2,5 раза (по скорости) – колебания лунно-земных суток ≈ ±24", колебания напряжённости Δg_н ≤±0,0034g_н . Это второе или гравитационное возмущение от Солнца.

Данные колебания суток и скорости могли быть частично обусловлены  солнечным эфирным ветром, о котором уже говорилось ранее. Пока неизвестно соотношение влияния гравитации и ветра. Это третье возмущение от солнечной компоненты эфирного ветра.

4 возмущение. От орбитальной солнечной силы.  Относительно солнечной системы координат Луна движется по волнообразной кривой орбите с переменным радиусом  R. Но кривизна имеет всегда одинаковый знак – центр и радиус кривизны всегда находятся внутри орбиты. На рисунке 28 это искажено из-за невозможности соблюдения масштаба всех элементов рисунка.

Центр масс системы «Земля+Луна» движется вокруг Солнца по радиусу R_цм, а Земля и Луна вращаются вокруг этого центра. R_л – радиус вращения Луны.

За счёт орбитальной силы (3.4) скорость Луны (в солнечной системе координат) будет изменяться. Из-за малости угла ψ и по формулам 3.4.2.6 и 3.4.2.2 можно записать: F_орб ≈ F_окр= -m·V_R·ω. Здесь: V_R –радиальная скорость Луны (относительно Солнца), ω – угловая скорость орбитального движения Луны вокруг Солнца.

Эта сила даёт (в результате расчёта) средний момент вращения относительно центра масс  системы «Земля+Луна»: .

При движении вверху от точки о₁  до точки о₃  (в III четверти) скорость Луны возрастает. В следующей IV четверти орбитальная сила тормозит Луну  в движении вокруг центра масс. В I четверти – разгоняет, во II – тормозит.

После вычислений получается, что скорость должна изменяться от воздействия переменного момента за четверть периода на ΔV= 38 м/сек.

В новолуние и полнолуние скорость Луны – наименьшая, а в квадратурах (точки 1 и 3) –наибольшая (за счёт данного солнечного воздействия).

Теперь опять обратимся к наблюдениям. Они в сочетании с анализом астрономических календарей показывают, что сумма скоростей в квадратурах больше, чем в сизигиях. Величина отклонения лунных суток приближается к ±1' (знак + соответствует отклонению в квадратурах). Величина изменения скорости определяется по формуле 4.2.1 и   соответствует должному теоретическому изменению (38 м/сек).

Это четвёртое возмущение позволяет объяснить причину того, почему Луна не падает на Солнце.

Когда Луна в новолуние находится между Землёй и Солнцем, сумма четырёх сил от Земли и Солнца, действующих на Луну (две -  гравитационные и две – центробежные), даёт неравенство – Луна тяготеет к Солнцу с разницей сил, примерно, в 3,9%  (если отбросить из рассмотрения данное 4 возмущение).

Именно это возмущение спасает Луну от падения. Уменьшение её скорости в новолуние (на 38 м/сек - по сравнению со скоростью в квадратурах, на 19 м/сек - по сравнению со средней скоростью) уменьшает центробежную силу Луны относительно Земли на 3,8 % (по отношению к среднему значению) и немного увеличивает центробежную силу относительно Солнца. Этого, в соответствии с проведёнными вычислениями, достаточно! 

Аналогичное саморегулирование динамики движения Луны происходит и в полнолуние. Луна улетела бы прочь – не будь возмущения от орбитальной солнечной силы.

Земля при этом повторяет движения Луны по тому же принципу, в такт с Луной. Под действием орбитальной силы обе разгоняются и тормозятся одновременно.

5  возмущение.  При наличии орбитальных ускорений Луны по земной орбите происходит изменение инертной массы Луны. Ускорения равны, в среднем, 0,17 мм/сек². Этого достаточно в данных условиях, чтобы уменьшить инертную массу Луны на 9,6 %.

За счёт этого уменьшения массы ускорения увеличиваются (по сравнению с кеплеровскими). Соответственно, скорость в перигее увеличивается, а в апогее уменьшается на 2,75 % (ΔV=±27,6 м/сек). Отклонения  лунно-земных суток составили ±1,5' (лето 2003 года).

Изменение скорости определяли по формуле 4.2.1.1, а затем определяли изменение инертной массы по формуле:            .                     (4.2.3)

В числителе написаны изменения кинетической и потенциальной энергий Луны при её движении от апоцентра (апогея) к перицентру (перигею), в знаменателе – среднее значение её кинетической энергии. Изменение потенциальной энергии определялось с учётом данных астрономического календаря (радиусы орбиты Луны) и наших значений геоцентрической константы. Это изменение вычислялось по формуле:

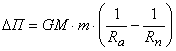.           ( 4.2.4)

Отрицательное значение выражения 4.2.3 будет означать, что масса уменьшилась, положительное – увеличилась.

Следует иметь в виду, что изменение инертной массы происходит только от орбитальных ускорений, только от изменения кинетической энергии относительно эфира. Изменение направления скорости не имеет влияния на инертную массу. Например, при равномерном вращении велосипедного колеса в вертикальной плоскости нет изменения инертной массы, хотя есть ускорения точек относительно Земли. У колеса в этом случае меняется только сила тяготения (3.9 и  3.10).

6 возмущение. При движении Луны с Землёй вокруг Солнца происходит также изменение их инертной массы. Но изменения эти малы (см. параграф о возмущениях планет 4.3).

7 возмущение.   Годовое (у астрономов – годичное неравенство). При движении центра масс « Земля+Луна» вокруг Солнца возмущения от воздействия Солнца будут меняться в соответствии с представленными формулами.

При этом будет меняться и эксцентриситет Лунной орбиты, как от изменения солнечных возмущений, так и от вытянутости орбиты, обусловленной различным притяжением Солнца. Следовательно, в течение года будут меняться и возмущения от Земли.

Это годовое возмущение не является самостоятельным, оно лишь объясняет непостоянство других возмущений.

Полный период изменения возмущений Земли не равен 1 году. Это обусловлено тем, что год (по времени) не кратен лунному месяцу (ни синодическому, ни сидерическому, ни аномалистическому…). Динамические параметры движения Луны складываются как переменные  функции с различными амплитудами и частотами.

Главное возмущение  Луны – эллиптическое. Связано с изменением скорости по  орбите в связи с её эллиптичностью (в соответствии с законом Кеплера). Изменение скорости происходит под действием орбитальной силы в соответствии с формулой 3.4.2.6 (см. также пар. 4.1.2).

Первые семь возмущений рассмотрены относительно движения Луны, возмущённого этим главным неравенством - отклонением от движения по окружности.

Возмущение 1 показывает изменение напряжённости гравитационного поля  (следовательно, и гравитационной «постоянной») в больших пределах (±34%).

 Возмущения 2, 3, 4, 6 – солнечные. Изменения скорости Луны по орбите за их счёт, в целом, скомпенсированы и не могут изменить периода обращения, который входит в формулу определения константы 4.1.3.1 (под константой  теперь понимаем её осреднённое значение за период обращения). Следовательно, заниженное значение гравитационной константы (на 2 %), определённое по движению Луны, по сравнению со стандартным (лабораторным) значением, является всё более объективным  и реальным фактом. 

Все возмущения имеют эфирную природу, согласуются с истинным движением Луны, которое, по нашим наблюдениям, имеет отклонение от расчётных данных астрономических календарей. Отклонения календарей от истинных движений обусловлены недостаточной ясностью физики движения Луны. Календарные расчёты базируются на пустоте Ньютона, на геометрической трактовке физических явлений, в некоторых случаях – на теории относительности. В астрономии наблюдается стремление совершенствовать математическую модель расчёта на основе наблюдений. Но пусть в этом участвует и физика!

В главе 5 (об аномальных явлениях) представлен  ещё один  случай удивительного поведения Луны.

Требуется большое число точных наблюдений за параметрами движения Луны (скорость, расстояние…), их дальнейшая обработка с применением компьютерной техники и уточнение  представленных здесь принципов.

 

4.3. Возмущения планет и роторный движитель

Возмущения  Земли и других планет обусловлены Солнцем и эфиром.

Главное возмущение Земли (и других планет) аналогично главному возмущению Луны – изменение скорости по орбите в соответствии со 2 законом Кеплера. Изменение скорости происходит под действием орбитальной силы (пар.3.4.2 и 4.1.2).

Последующие возмущения, как и в предыдущем параграфе, рассмотрим относительно  кеплеровского движения.

Возмущение 1. Гравитационное возмущение от Солнца Земля  (и другие планеты) получает так же, как и Луна от Земли (1 возм. Луны), получая при этом из эфира и энергию для своего движения по принципу диска.

Наши наблюдения не имеют отклонений от данных астрономических календарей при подъёме (движение от перигелия к апогелию) и опускании (движение от апогелия к перигелию) Земли. Но сами календари свидетельствуют о разнице скоростей: при подъёме скорость Земли больше, чем при опускании.

Средняя разница скоростей подъёма и опускания (за 4 последних годовых цикла, 2000 ÷2004 г.) составила 1 % от средней орбитальной скорости.

Разница скоростей в средних точках земной орбиты 1и 3 (рис.27) составит 1,57 % от средней скорости. Применив формулу 4.2.2, получим Δg_н = ±0,46g_н . То есть, среднее изменение напряжённости поля и тяготения  к Солнцу достаточно существенное :  ±46% или в 2,7 раза. Положительное значение (утяжеление) соответствует движению Земли во II и IV четвертях земной орбиты, отрицательное (облегчение) – в I и III четвертях .

В I четверти Земля ускоряется от Солнца, во II – тормозится, в III –ускоряется к Солнцу, в IV- тормозится (см. также пар.3.4.2). То есть, радиальные ускорения имеют пульсирующий характер, как и точки диска относительно Земли. Речь опять идёт об истинных ускорениях, а не о фиктивных центростремительных, введённых в механику ошибочно.

Именно эти (радиальные) ускорения, наряду с другими производными движения,  и определяют изменение силы тяготения к Солнцу.

Возмущение 2  обусловлено изменением инертной массы Земли (и других планет) от воздействия орбитальных ускорений, что приводит к изменению её скорости.

Обоснование такого суждения заключается в том, что не выполняется закон сохранения энергии при орбитальном движении планет, в разной мере.

У Плутона изменение потенциальной энергии за полупериод обращения на 7 % больше, чем кинетической; у Меркурия – на 4.3 %. У других планет – менее 1 %.

Меньшее изменение кинетической энергии планеты, по сравнению с потенциальной, можно объяснить увеличением инертной массы планеты (другие объяснения противоречивы). То есть, все планеты увеличивают свою инертную массу. Земля и Нептун увеличивают всех меньше, практически, без изменения. У Меркурия (в соответствии с формулой 4.2.3) она увеличена на 4.3  %,  у Плутона (больше всех) – на 7%.

Возмущение 3  обусловлено вращением планет. Этот роторный эфирный эффект напоминает эффект Магнуса в аэродинамике.

Планета – это вращающийся вихрь эфира, который взаимодействует со встречным потоком эфира.

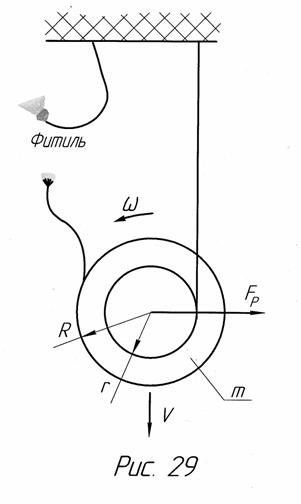
Наши первые опыты по падению цилиндров с вращением дали основание для продолжения экспериментов. Образно говоря, сила Магнуса тяжёлого цилиндра превысила силу Магнуса лёгкого цилиндра (рис29). Две параллельные нити наматывались на концы цилиндра с радиусом r ≤ R . Затем цилиндр раскручивался и падал под действием  своего веса. При этом возникает сила F_р.

Эту силу F_р тяжёлого вращающегося тела (после вычета из неё силы Магнуса) назовём роторной  силой.

Физическая основа этой силы заключена в разнице давлений эфирного встречного потока слева и справа. Левая часть потока тормозится частицами  (амерами) вращающегося цилиндра. Правая часть потока не испытывает такого торможения, а наоборот, при больших скоростях вращения ускоряется этими частицами. Таким образом, скорость левого потока меньше скорости правого потока. В соответствии с принципом Бернулли, разница скоростей потока  и порождает разницу давлений.

На рис. 30 дана схема роторного движителя. Наш первый движитель на плоту дал силу тяги около 25 граммов и плот с человеком стабильно двигался.

Для большей убедительности, движитель при испытаниях можно поместить в закрытый ящик, чтобы полностью исключить воздушную тягу.

Сила роторного движителя в наших опытах соответствовала формул

F_р = kωVm .                          (4.3.1)

Здесь: k – коэффициент роторной силы, зависящий от материала, размеров и формы тела, от плотности и вязкости эфира и т.д., ω – угловая скорость вращения ротора относительно своей продольной оси, V – скорость перемещения центра масс отдельного ротора, m – масса ротора.

    

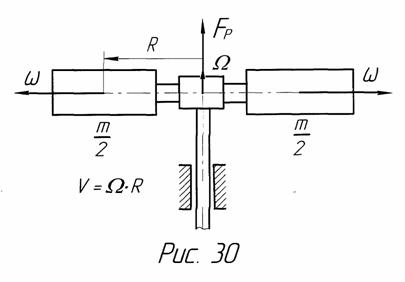
Для вращающихся планет k =,                                           (4.3.2)

где  – отклонение коэффициента напряжённости гравитационного поля от «стандартного» значения по закону тяготения   =F/m.                  (4.3.3)

Сила тяготения .                                                        (4.3.4)

Для Юпитера коэффициент k = 1,8·10 ^–5 получен из сравнения движения Венеры и Юпитера (на основании данных астрон. календаря за 2004 год). Венера вращается пренебрежимо медленно, поэтому её гелиоцентрическую константу GM_с можно принять за истинную.     

Отметим, что, по нашей концепции, масса Солнца М_с  на 2 % больше общепринятого значения, исходя из методики определения этой массы (74) и нашего значения гравитационной константы G, которое меньше стандартного значения на 2% (см.4.1.3).

В силу сказанного, гелиоцентрическая константа, определённая по движению Венеры, совпадает с её стандартным значением GM_с = 132712438·10¹² м³/сек².

По Юпитеру константа больше на 0,18 %. Другие планеты дают также большие значения по сравнению с Венерой. У всех у них гравитация усиливается роторным тяготением. Константы тяготения имеют разброс в одну сторону – завышения.  Вычитание роторного эффекта из общего тяготения (по приведённой далее формуле 4.3.6) выравнивает гелиоцентрические константы, определённые по разным планетам.

 У Нептуна  коэффициент роторной силы k  в 1,5 раза больше, чем у Юпитера.

Как было уже отмечено, этот коэффициент зависит от размеров роторного тела. В опытах с цилиндрами он в 17 раз больше, чем у Юпитера. То есть здесь, уже не  первый раз, прослеживается та концепция, что с ростом размеров тела его динамическое и сравнительно кратковременное взаимодействие с эфиром ослабевает. Имеется в виду, что ослабевает относительное взаимодействие – на единицу массы тела. Конечно, в данном случае может накладываться влияние разницы плотности земного и солнечного эфира, если эта разница существует.

Для каждой планеты выполняется соотношение трёх радиальных сил – тяготения, роторной и центробежной, соответственно:  F + F_р =F_ц .                           (4.3.5)

После подстановки: 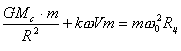 ,  где ω_{о -} угловая скорость орбитального движения планеты, ω – угловая скорость вращения планеты относительно своей оси, R_ц – радиус орбиты относительно центра вращения, для планет R_ц =R .  После сокращения и подстановки получим:    .                 (4.3.6)     

Здесь: С – константа данной планеты, включающая роторный эффект, GM_с – стандартная гелиоцентрическая постоянная.

3-й закон Кеплера (только для планет) запишется:  .          (4.3.7)

В настоящее время необходимы лабораторные эксперименты с более мощными роторными движителями, чтобы получить большую уверенность в роторной эфирной силе. 

 

4.4.Вращение планет

В параграфе о гравитационных двигателях уже говорилось о способности вертикального диска получать энергию гравитационного поля Земли (или другого тела).

Планеты при вращении вокруг своих осей получают энергию по принципу диска из эфирного гравитационного поля Солнца. Направление вращения планеты не имеет значения.

Как было отмечено, большой диск вращается лучше. Самая большая планета Юпитер также вращается с наибольшей скоростью. За ним по размерам идёт Сатурн – он же уступает Юпитеру и по скорости вращения, но только ему. Все планеты-гиганты вращаются с большими угловыми и окружными скоростями. У малых планет – малые скорости.

Конечно, диаметр планеты не единственный параметр, определяющий скорость её вращения. Но эта тенденция прослеживается.

Например, Уран почти лежит на боку и поэтому его вращающий момент мал (сравнительно своих гигантов-собратьев). Но! он вращается быстро. Однако! Быстро он вращается за счёт ранее накопленной скорости. В настоящее время скорость его вращения быстро замедляется. За последние десятилетия его звёздные сутки увеличились от 10,8º до 17,28º. Это свидетельствует о том, что вращающий момент его  всё-таки мал, что этот момент меньше момента сопротивления  внешней среды.

Аналогично тормозится и Марс.

Атмосфера влияет на сопротивление, что способствует вращению Марса (у него слабая атмосфера) и препятствует вращению Венеры с её сравнительно мощной атмосферой.

В 18 веке, не вникая в перипетии эфира, работали над большими самодвижущимися колёсами известные германские изобретатели Иоганн Орфиреус и Гертнер. Работа колёс привлекала внимание многих просвещённых людей Европы, в том числе и Петра 1.

Колёса осматривали профессор Вольф (учитель Ломоносова), физик Гравезанд, Лейбниц и многие другие. Они не нашли обмана, что следует из их докладных записок и переписки Лейбница с Ньютоном. Польский король Гессен Кассельский выставлял караульных гренадёров, комнаты с  колесом осматривались и опломбировывались – машина Орфиреуса работала 14 дней, после этого – 40 дней, затем – два месяца без затухания. Затухание же колеса можно обнаружить достаточно быстро.

Была объявлена премия тому, кто разоблачит обман.  «Разоблачители», конечно, нашлись.

А мы, как уже говорилось, провели опытные исследования – колесо Орфира, в принципе, могло вращаться.

 

Глава 5. Аномальные явления

Мне было лет 20. Шёл по тракту у села Можги к городу Можге, в Удмуртии. Увидел зарево в полнеба – словно горел город Можга в ужасном пожаре. Постепенно зарево превратилось в пылающий шар, который медленно опустился и скрылся за ближним бугром. Была весенняя распутица, и я не пошёл по полю искать место посадки, возможно, сомневаясь в наличии каких-либо следов, поскольку был проникнут внушённой примитивной мыслью, что ничего необычного и необъяснимого наукой быть не может.

Но впечатление было восхитительное. Впервые ощутил реальную возможность сказки, почувствовал какой-то новый смысл.

Пришёл в город Можгу, спросил у одного мужика на вокзале, не видел ли чего такого. Нет, говорит, не видел. А сам на меня подозрительно так смотрит. Больше ни у кого спрашивать не стал.

Другой случай. Над стадионом днём видел облако. В облаке горели огоньки, как звёздочки. Позднее встречал людей, видевших подобное.

Светящиеся шары видели многие из тех, кого знаю. В нескольких случаях шары висели подолгу – по несколько суток.

Несколько человек видели по две Луны.

Школьники  и взрослые рассказали сотни случаев об НЛО. Половина из них похожа на правду.

Иногда шары взлетали, иногда садились, иногда от них отходи лучи вниз или в стороны. Иногда в небе появлялись причудливые змейки, зигзаги, повторяющиеся траектории светящихся тел, спирали и т.д.

Сергей из деревни Кварса и его друг два часа бегали за шариком, который развлекал их, вырисовывал различные геометрические фигуры, обозначил контур водокачки на большом расстоянии за ней. Друзья подходили к шарику, а он исчезал и появлялся далеко с другой стороны.

Такое разумное и безобидное поведение шариков наблюдали и другие, согласно информации СМИ.

Вениамин Поторочин приехал из посёлка Ува и рассказал о большом аппарате, у которого было видно несколько двигателей, из которых выходили светлые лучи тумана.

Две сестры Аншаковы видели пролетающий большой дирижабль за северной частью нашего города. Знакомый майор КГБ проработал этот вопрос на республиканском уровне и удостоверил в отсутствии официальных пролётов дирижаблей. Да и откуда им взяться здесь? Состояние этих дел было достаточно хорошо известно.

Тёмным вечером в  сентябре 1989 года я видел мощный прожектор, освещавший пруд сверху, свет от него расходился конусом. Объект летел над прудом на высоте около 50 метров, иногда выключался – в это время к нему подлетали мелкие светящиеся шарики снизу от водной поверхности пруда. Всё это видели и заводские охранники вместе с начальником караула старшим лейтенантом М. Баженовым, но с другого направления так, что мы полностью определили местоположение объекта. Объект видели в воинской части и в г. Ижевске.

Венера Мигунова (работница хлебозавода) сообщила в том же 89 году, что она и её дочь наблюдали шары, но в разное время. Мать видела 4 шара, которые спускались по заводской трубе. Другой раз шар диаметром 1-2 метра сильно свистел так, что она проснулась.

Дочь видела шар у квартиры, что недалеко от телевышки. Сверху шара – пламя, снизу – луч. Глаза дочери налились кровью. Они были после операции и болели. Через 2-3 дня всё прошло, глаза выздоровели.

Неля Тетерук (сотрудница штаба гражданской обороны) и её четырёхлетний сын видели «тарелку» в 1989 году, пролетала над улицей Кирова. Отчётливо видны были красные огни, загоравшиеся поочерёдно, ножки и контуры, более тёмные, чем небо. Был слышен гул 2-3-минуты. Высота полёта – небольшая. Угловые размеры объекта – раз в 5 больше Луны.

Следующий случай из 89 года. Вначале НЛО наблюдали в бинокль мои кружковцы: Олег Мамрыкин и Олег Подшибякин, находясь в субботу у бабушки. Объект «пришёл» с Ижевска, дошёл до заводской трубы, сделал манёвр, развернулся  и направился опять в сторону Ижевска, уже против ветра. Здесь его заметили и мы (со мной был сын), находясь на пруду. Дело было днём, после обеда. Ребята в бинокль заметили, что с  одной стороны диска светился огонёк. Цвет диска был серебристо-металлический, затем он стал золотистым, мы его увидели именно таким. Ребята заметили также, что объект менял свою форму. Газета «Удмуртская правда» сообщила, что видели такой объект в городе Ижевске в тот же день, но утром, низко над домами, он уходил в нашу сторону Воткинска. Длина его – около 20 метров, что соответствовало нашим наблюдениям.

Я стал внимательно наблюдать. Сотни рыбаков азартно следили за своими удочками, не поднимая голов. Объект медленно пролетел  над городом и скрылся за возвышенностью. Тотчас в этом же месте появился самолёт и пролетел в сторону Шарканского залива в километре от нас. Ветер шёл от самолёта, но мы не услышали звука его мотора, мы не заметили его крыльев, как не старались. Профиль фюзеляжа, примерно, как у самолёта АН-2. Минут через 5 самолёт пролетел в обратном направлении, скрылся за той же возвышенностью, где появился вместо диска. И опять там же поднялся золотистый диск и «поплыл» по небу в сторону Ижевска.

Если мы просто не рассмотрели крыльев самолёта, то его экипаж должен был видеть этот диск. Это было 11 ноября. Сожалею, что не нашёл тогда возможности съездить в аэропорт.

Два Олега видели в тот день в бинокль ещё один объект, который вечером слился с Луной.

8 и 9 мая 1999 года плоскость нашего небесного меридиана пересекла край диска Луны в одно и то же время (утром) с точностью до одной минуты. Время фиксировалось и сверялось с помощью трёх механизмов (часов и радио).

Известно, что средне-суточное запаздывание этого явления составляет  50,5 минут (пар.4.2). Это означает, что в орбитальном движении относительно Земли Луна в эти сутки полностью затормозилась.

В последующие дни Луна увеличила свою орбитальную скорость, компенсируя задержку. В один из предыдущих дней скорость также была высокой.

Нас, естественно, интересуют данные астрономов, проводивших аналогичные нашим или подобные (по числу лунных покрытий) замеры скорости Луны в эти дни. Нас интересует, проводятся ли вообще где-нибудь аналогичные замеры. Наши письма астрономам пока не дали положительного ответа на этот вопрос.

Нам интересно было бы знать, как часто астрономы замеряют скорость движения Луны.

Не исключено, что это могло быть одно из очень редких и сильных возмущений лунного движения.

Гаврилов Алёша и его два товарища из 2 класса в декабре 1989 года наблюдали утром объект у телевышки, угловым размером с Солнце, на высоте 40-50 метров (рис. 32).

Свет в их доме и в детском садике, что рядом с домом, погас. Снег и ребята (они были во дворе, направляясь в школу) были освещены жёлтым, а затем синим цветом. После того, как объект улетел, свет снова зажёгся.

Ребята всё рассказали поочерёдно в отдельной комнате. Противоречий в рассказе и в ответах на мои вопросы совершенно не было. Всё это видела и мать Серёжи Дианова (одного из очевидцев).

Подобные явления  достаточно распространены, демонстрируя иногда некоторые отличительные элементы или свойства.

В марте 1990 года я и мой сын Андрей видели па пруду следы длиной 49 сантиметров, шириной –16 см. Они были вплавлены в лёд на глубину 1-2 см. Следы пересекали Шарканский залив, походили на след большого человека в калошах. Контуры были ровными и гладкими.

Пройдя сполкилометра, обнаружили 2 цепочки круглых следов (рис.33). Никакого развала следов (как у животных) не было. Цепочки следов шли поперёк залива, перекрещиваясь или расходясь, подходили к роднику. Возможно, это был один объект, который прошёл вперёд и назад. Снег вокруг следов везде лежал нетронутым.

В апреле 1990 года  шёл поздно вечером в совершенно отчаянном настроении. Но вспомнились многозначительные слова песни Высоцкого: «Мы золото отнимем у чертей, свои котлы топить им будет нечем». И мне подумалось: «…да где же ты, Владимир? Ну появись, хотя бы в виде облачка!».

На пруду ещё лежал снег, небо – чистое со звёздами, и  «Луна так нарядно светила».

И вот на этом чистом небе в это мгновение, в том месте, куда я посмотрел только что, вдруг возникло облачко, в ста метрах от меня. Оно росло быстро и разрывалось трассирующими осколками. Один осколок вылетел с невероятной скоростью и улетел далеко вверх и на запад, как метеорит. Облако светилось необычным серебристо-белым цветом. Я, постояв, пошёл по берегу – облако стало двигаться вслед за мной, метров 400. Тогда я остановился. Облако дошло до меня и растаяло над головой.

« Не единой буквой не лгу.

Он был чистого слова слуга,

Он писал ей стихи на снегу.

К сожалению, тают снега…»

Иван Григорьевич Фёдоров, пенсионер, в прошлом – сварщик, пришёл в наш клуб и рассказал о давней встрече с НЛО. 30 лет он ходил по редакциям и другим учреждениям, но его никто толком даже не выслушал. У меня не было оснований не доверять этому человеку, скорее – наоборот.

Иван своей рукой зарисовал в моей тетради аппарат, который медленно «проплыл» около него в нескольких метрах  (рис 34).

Дело было в городе Тиммертау Казахской ССР в августе 1964 года. Иван стоял на балконе. Появилась «тарелка» диаметром около 3 метров, высотой около 1,5 метров. Он рассмотрел отдельные детали. Верхняя «застеклённая» часть тарелки светилась сине-зелёным цветом. Слышался шум воздуха или газа.

Аппарат пролетел и скрылся за домами.

 

Другой случай рассказал Слава – сторож строящегося загородного холодильного комплекса. В девяносто первом году мы с кружковцами неподалёку проводили эксперименты с махолётом, хотели заночевать в палатке, но Слава не позволил мёрзнуть на песке и пригласил в своё помещение.

Однажды он шёл с рыбалки вдоль нашей небольшой реки Сивы. Увидел «банку» на опорах. Рядом – люди в каких-то водолазных костюмах. Спросил, чего они тут хотят делать, подумал, что идут какие-то подводные работы. Они жестом показали, чтобы он шёл дальше. Слава пошёл, но всё же  обернулся  и переспросил. Тогда они «вырубили» его. Когда очнулся – никого не было. На месте опор – примятая трава.

Его жена рассказала, что её муж алкоголь не злоупотребляет, с рыбалки тогда пришёл трезвым и потом, уже полгода,  всё спрашивает -  что же это было? 

В деревне Курочкино Воткинского района Мария Васильевна выключила телевизор, свет и хотела лечь спать. В окно увидела, как по небу летят шары, соединяются в один большой «сноп». И этот сноп садится перед её домом, в 30 метрах. Об этом писала газета «Ленинский путь», а я позднее встретился с Марией.

Сноп превратился в зонтик, по её словам. У зонтика появилось шесть фигур, одетых как танкисты времён отечественной войны, в шлёмах. Четверо стали спускаться к прудику, общаясь между собой, а двое направились к ней, постучали в дверь в сенях. Мария схватилась за скобку, удерживая дверь, раздумывая, как быть. Собака, которая всегда лаяла при посторонних визитах, на этот раз молчала.

Когда решилась пустить гостей в дом, было уже поздно – они исчезли вместе с зонтиком. Теперь жалеет, что долго мешкала тогда.

Ромбический объект раздавил крышу подсобного помещения в детском садике Воткинска – её потом ремонтировали. 

Проволока (диаметром 2 мм, длиной 1,5 метра) маятника удлинилась на 30 мм под действием груза маятника  весом 3 кг, изменился период колебаний. После снятия груза (шара) длина проволоки восстановилась (через сутки), восстановился прежний период колебаний маятника.

 

Головка болта диаметром 12 мм прошла через отверстие под стержень болта диаметром 8 мм (от лёгкого усилия моей руки). Чтобы поставить болт на прежнее место, нам пришлось снимать и разбирать рукоятку токарного станка.

Затяжной винт рубанка был обильно намазан маслом на наших глазах.

Шпангоут фюзеляжа махолёта «Джордано», который сильно измучил меня вечером, утром оказался перерезанным внизу, в той точке, которая вызывала сомнения и мучения. В клубе никого не было всё это время. Мы убрали шпангоут  из конструкции.

Утром пришли в клуб – на чертёжной доске сидела «рыжая шапка» несколько секунд. Исчезла.

Циркуль разводился несколько раз неведомой рукой на нужный размер при копировании деталей со сборочного чертежа. Это случалось, когда я после небольшого перерыва приступал к новой детали.

Мы, вдвоём с сыном, на берегу слышали, как в его пустой рыбацкой сидухе на спине сильно бьется рыба. Я услышал и спросил у него, не показалось ли ему что-либо сейчас.  Он чётко подтвердил услышанное мною.

Идя с работы зимним вечером, видел взметнувшийся к небу фонтан огня из полыньи у берега пруда по улице Мира, 5.

Летом наблюдали вертикальные молнии в ясном дневном небе. И вспомнилось вечернее размышление Михаила Ломоносова:

«Что зыблет ясный Солнца луч? Что тонкий пламень в твердь разит?

Как молния без грозных туч стремится от земли в зенит?

Как может быть, чтоб мёрзлый пар среди зимы рождал пожар?»

Однажды осенью, днём, шёл по лесной дороге к лагерю «Чайка». Обернулся на появившийся звук автомашины и увидел человека среднего роста в серой куртке с прямоугольными плечами, который шёл за мной с необъяснимым выражением смуглого лица, в кепке с опущенными краями.

Затем он развернулся на пол-оборота и побежал от меня, широко размахивая руками. Голова его исчезла, виднелась только линия плеч. Это сильно бросилось мне в глаза. Он повернул налево – в сторону от дороги, в кусты, из которых, вероятно, и появился. Наблюдая теперь за его профилем, видно было мелькание веток деревьев там, где должна быть его голова.

 

Выводы по эфироидам

Эфир является неиссякаемым источником чистой энергии. Найдены и обоснованы способы её получения на земле и в космосе.

Предлагаем три варианта эфирных движителей: центроид, инерцоид и роторный движитель.

Возможно их применение на земле и в космосе.

Взаимодействие материальных тел с эфиром на земле рассмотрено с помощью экспериментальных установок и многих вычислений и сравнений с движением небесных тел.

С позиций эфира изложена физическая суть неравномерности движения Луны, Земли и других планет.

Уточнено представление об ускорениях.

Изложена эфирная природа таких понятий, как центральная и центробежная сила, сила инерции, сила тяготения.

Уточнён и дополнен закон всемирного тяготения, закон импульсов, закон сохранения энергии, теорема Кориолиса.

Обнаружена существенная зависимость сил тяготения и инерции от кинематики движения (скоростей, ускорений и их производных).

Обнаружен волнообразный характер гравитационного взаимодействия эфира с движущимися телами.

Установлено, что на махолёт  действует несколько эфирных факторов, повышающих его подъёмную силу, тягу и экономичность полёта.

Проведён сбор материалов по аномальным явлениям в Воткинском районе, часть которых представлена в данной работе. Непознанные существа и явления могут быть разумными и стихийными, как и все известные проявления жизни на Земле. Разумные существа идут на разумный последовательный контакт. Поскольку эти существа имеют эфирную структуру, они могут жить среди нас, в космосе или на соседних планетах.

Эфир – это живой организм в самом широком смысле. Из него состоят все видимые и невидимые вещества, им движутся, его законам подчиняются. Он бесконечен как внутрь, так и наружу. Невозможно узнать все его свойства, но он позволяет постичь то, что нам необходимо сегодня.

Иначе говоря, эфир – это субстанция, то есть первооснова всех вещей и явлений.

Эфир проявляет себя в телерадиосвязи, оптике, химии, физиологии, электродинамике…

Мы предложили факты механики, которые доступны опытной проверке.

Колебания каждой частицы, как угодно малой, распространяются во всех направлениях до бесконечности. Поэтому поведение любого объекта, в том числе и человека, может быть известно в любой точке мирового пространства. Пространство не может не реагировать на наше поведение. Мы получаем ответные сигналы, отработанные вселенской материей в соответствии с её законами.

 

Фотоприложение «Наши стоянки»

Фото 53. У речки Сидоровки, где было много шампиньонов и блушники, в 1988 году.

Фото 54. Станислав Авдеев фиксирует кинокамерой движение «Истины».

Фото 55. Интервью американских журналистов у лётчика-испытателя «Истины» Владимира Макагонова. Москва, Тушино, 1987.

Фото 56. Андрей Знатнов (справа) рассказывает о вихрях вокруг махолёта (ему приходилось их измерять руками, ногами и даже носом).

Фото. 57. Пробежка самолёта «Nansen», 1981 год.

Фото 58. Чувство полёта рождается на земле. Два Андрея в пионерском лагере «Юность» построили и запустили по одной модели планера и по одной кордовой модели самолёта с керосиновым двигателем, 1984 год. Уже через 2 года Андрей Знатнов (ученик 8 класса) успешно производит полную сборку редуктора «Истины», вникает во многие тонкости авиационной механики.

Фото 59. В метляковском провансе. К испытаниям готовятся 2 махолёта. Слева – «Джордано 3».

Первые дни в лагере. Строим кухню, ангар… затем занимаемся махокрылами.

Фото 60. У села Первомайское, 1991 год. Последний день испытаний

Фото 61. Махолёт «Джордано».

Фото 62. В спотзале техникума. Первая общая сборка и испытание аппарата ночью в декабре 1990 года.

Фото 63. При скорости встречного потока воздуха 10 м/сек (иногда – меньше) при махании аппарат мог отрываться от земли. Для взлёта с неподвижными крыльями требовалась скорость 14 м/сек.

Фото 63а. За Конанком. Исследовалась работа «Джордано» с большой амплитудой махания, с принудительным закручиванием крыльев по размаху, с помощью механизма, действующего синхронно с мускульным приводом. Оба фактора повысили удельную тягу крыльев. Для повышения абсолютной тяги требовался редуктор. Прямо в лагере переделали аппарат по схеме «Джордано-2» и получили обнадёживающие результаты.

Фото 64. Он хотел подниматься, но крен прижимал…

Фото 65. Флюр и его птица следуют за буксировщиком.

Фото 66. Двигательная установка махолёта «Невидимка». Изначально разработана для орнитоптера «Элона».

Фото 67. Саша Корякин с моделью планера А-2 с отведёнными назад съёмными консолями крыльев. В правой руке он держит прямые консоли. Лётный эксперимент показал преимущество косых консолей по времени полёта на 30%. Они повышают устойчивость модели. Они уменьшают сопротивление крыльев по тому же принципу, что и гибкая задняя кромка – возникают мелкоамплитудные высокочастотные автоколебания крыла с участием вихрей воздуха и его внутренней энергии. И всё это слышно при полёте модели (или большого крыла).

Фото 68. Три Икара на берегу р. Сивы. Слева направо: Андрей Краснопёров, Артём Ложкин (с махолётом), Слава Белоногов (с моделью планера «Звёздочка»)

Фото 69. Модель махолёта вертикального взлёта «Стрекоза». Крылья шарнирно поворачиваются относительно своих продольной осей. Изготовил, испытал и доработал Антон Попов

Фото 70. В воздухе модель Артёма Ложкина «Алабино», 2002 год.

Фото 71. Сборка махокрыла «Влади». При махании крылья вращаются по кругу, человек стоит на пирамидке. Усилие крыльям передаётся через руки и ручку, совершающую вертикальные движения вместе со сборной втулкой, к которой крепятся подкосы крыльев.

Фото 72. На этапе создания «Азазель» слева направо: Юра Белый, Артём Ложкин, Антон Попов, Владимир Крылов.

Фото 73. Проверка работоспособности и силы тяги крыльев.

Фото 74. У села Перевозное.

Фото 75. Махание крыльями от набегающего потока воздуха.

Фото 76. Слава настраивает аккумуляторы.

Фото 77. В берендеевом царстве.

Фото 78. Артём,Слава и Антон собрали установку по уточнению принципов механики.

Фото 79. Андрей докладывает на конференции об инерцоиде «Бернулли» и инерцоиде «Жюль Верн» (виден только его фрагмент). «Бернулли» катался по полу и плавал на плоту. «Жюль Верн» плавал и катался без всяких переделок. Направления движения на воде и на полу были одинаковы.

Фото 80. Юрий Белый – студент московского авиационного института. В этом году защитил диплом инженера. Участник Кизел-кытлымской экспедиции и других исследований.

Фото 81. Гора «Косьвинский Камень», на вершине которой производились замеры.

Фото 82. Замеры гравитации в шахте.

Фото 83. Долина, где течёт р. Сива, где сторож Слава встретился с необычным объектом и его экипажем. В этой долине жители д. Кварсы наблюдали летающие треугольники и шары.

Фото 84. Фрагмент фотоснимка с большого расстояния - как и последующие фото. Махолёт находится в свободном полёте после разгона катапультой (иногда разгоняли снегоходом).

Фото 85.

Фото 86.

Фото 87.

Фото 88.

Фото 89.

Фото 90. Москва, Тушино.

Фото 91. Начало разбега. В кабине – Владимир Макагонов.

Фото 92. Скорость более 50 км/час, через секунду «Истина» на мгновение оторвётся от взлётной полосы.

Фото 93. Флюр на мускульном махолёте.

Фото 94. Пробежка «Джордано» с увеличенной амплитудой махания.

Фото 95. У Кельчинской дороги, 1993 год.

Фото последнее. Чиновник приезжал.

 

Заключительная часть

Выводы по махокрылам сделаны в конце 1 части, по эфирным явлениям – в конце 2 части. Здесь отметим лишь главную суть и остановимся на различных организационных вопросах и проблемах нашей темы о механике. 

Махолёты  могут стать  самыми экономичными транспортными средствами.

С помощью машущих крыльев можно получать энергию из атмосферного воздуха (газа)  на Земле и на других планетах и на этом принципе строить энергостанции.

Установлено колоссальное преимущество пульсирующих и других неустановившихся течений перед установившимися. Нестационарная аэродинамика способна спасти авиацию и энергетику от кризиса.

На движение махолётов оказывает существенное влияние мировая эфирная среда.

Основное современное производство энергии с прогрессирующими темпами заражает биосферу и само общество.

Учёные надеются обнаружить энергию с помощью ускорителей частиц. Во Франции ведётся строительство 28 километрового синхрофазотрона. Ведутся разговоры о строительстве 300 километрового подобного комплекса.

Кто-то измышляет возить гелий с Луны для холодного ядерного синтеза, для чего понадобилось бы больше половины мирового бюджета, при условии, что возможность получения энергии таким способом практически была бы реальна.

Мы же предлагаем  более простые варианты  поиска и получения энергии из воздуха и эфира. И разницу эту способен оценить любой смышлёный школьник.

Воздух и эфир могут дать чистую и дешёвую энергию, что позволит расширить все знания и повысить культуру.

Все современные физические теории мироздания опираются на ложную теорию относительности  Эйнштейна. Все они способны объяснить  частные факты, из которых они и выводились, но они не претендуют на всеобщее объяснение явлений физики. Математические выкладки оторваны от реальных физических процессов, что наиболее полно осознают инженеры – исследователи и физики - прикладники.

Планируются пилотируемые экспедиции на Луну и на Марс. Разорительно до невозможности летать туда на «керосинках», тем более, что обратный путь с Марса пока весьма проблематичен (не хватает топлива). Потратив малую часть этих средств на отработку эфирных движителей, мы укоротим время перелёта и вес аппаратов во много раз, избавимся от невесомости, поскольку у аппарата всё время будет сила тяги. Сначала - для разгона, затем - для торможения.

Работа движителей возможна от солнечных батарей, например, пока не будут отлажены космические эфирные энергостанции.

Грубое освоение планет негативно скажется на нашей жизни, науке, экологии. Да и политики, в итоге, потеряют. Вспомним слова С. П. Королёва: «Сделаешь быстро, да плохо – люди забудут, что сделал быстро, люди будут помнить, что сделал плохо…». Нам следует делать хорошо хотя бы для того, чтобы делать быстрее.

 По данным патентной службы США, около 95%  всех  ключевых  нововведений в науке приходится на долю изобретателей-одиночек, а не больших коллективов. Примерно, такие же показатели можно привести и по нашей стране, как сообщают представители официальной науки (77).

Новое рождается в подвалах и на коленках, в пыли, в эпоксидно-смоляном угаре, в нищете. Другие потом на этом делают деньги, в невежестве своём даже не подозревая, что у используемой разработки вообще мог быть какой-то автор.

Государственные предприятия и институты не способны заниматься перспективной наукой, поскольку они работают по строго «научному» плану в соответствии с известными законами. Здесь идёт прорыв в области технологий. И если что делается нового, то это за счёт опять же одиночек, совмещающих новаторство с основной работой.

И предприниматели ищут только готовые к продаже разработки.

И нет такой организации ни в России, ни на Земле, которая помогала бы решить материальные проблемы одиночек-изобретателей, работающих над темами, которые нельзя продать, но которые могут принести  пользу в будущем. 

Но она должна быть!

В мире много богатых людей. Почему бы кому-то из них не стать по-человечески разумным и счастливым на этом поприще. Ведь деньги он сделал за счёт других людей, за счёт матери-Земли, которая нуждается в нашем внимании.

Государства тоже могли бы выделить для этого какой-то разумный процент бюджета и  контролировать. В любой разумной, пусть даже бедной, семье бюджет предполагает расходы на приобретение знаний.

Скудеет техническое творчество школьников. На выставках  существенно преобладают вышивки, мягкие игрушки, рисунки и прочие творения женских рук. И они  могут исчезнуть.

Кто будет создавать корабли?!

Из институтов выходит дипломированный «шлак» на 99,9 % (по образному выражению генерального конструктора авиадвигателей Кузнецова). И этот один из тысячи – в прошлом юный техник или самодельщик, прошедший начальную (но очень важную) инженерную школу конкретного созидания.

Несколько мягче выражались другие известные авиаконструкторы (Яковлев, Антонов, Ильюшин…), но с такой же сутью. Они были от души рады, когда в их коллектив приходили бывшие авиамоделисты, которые, по их словам, никогда не станут бюрократами в науке.

При поступлении в технические вузы, как правило, оцениваются теоретические знания по предметам, на призвание к данной профессии, на увлечённость смотрят редко, очень редко.

В то же время, руководители технических кружков поставлены в весьма затруднительное положение как материально, так и снижением интереса учащихся к этому творчеству, так как мало интереса к ним у государства. «Если ты умный, то где твои деньги?» - один из принципов современного господствующего общества. Он исключает полноценное развитие науки и самого общества. Каков пример для юных! Я слышал от банкиров, что у каждого - своя истина. И многие так думают.  Приходится напоминать, что истина – она одна. Суждений - много. Истина нужна, чтобы жить в согласии с природой. Кто с этим не согласен, тот живёт  в ожидании катастрофы (прежде всего, личной катастрофы). Нашу общую истину нам следует искать в общем поиске знаний.

Например, всё финансирование нашего клуба (включая зарплату 2 сотрудников) за последние 20 лет составило в среднем  около 100 долларов в месяц. Дополнительно финансировалась аренда помещения  клуба площадью 100 м².  

А вот другой пример. Месячный доход директора предприятия (он урвал акции, пока его рабочие горбились в цехах, он получил дотации от государства…) иногда в сотни раз больше месячной зарплаты рабочего или инженера. А ведь напряжением ума или мускулов они отличаются не так сильно. Известно (в мировой практике), что умный руководитель назначает себе оклад, равный среднему на его предприятии. Такое предприятие начинает расцветать. Тогда работники сами повышают его зарплату. С таким директором и погибнуть совсем не страшно. Да и директору жилось бы лучше. А кто теперь рабочий для директора – рабочий скот, а кто директор для рабочего? То же самое, только без прилагательного и с другим окончанием, да в кавычках, что усугубляет определение. И здесь вспоминается Громов из «Угрюм – реки».

Чиновникам баснословно (по сравнению с «подлым» сословьем) повышают оклады, «чтобы они меньше воровали», меньше брали друг у друга взятки. И никто из чиновников от получения таких окладов не отказался. Правда, были редкие исключения в среде чиновников, кто возражал против разделения общества. И это радует. Но от получения окладов никто не отказался (к сожалению, мы таких  не знаем)

Чиновники считают, что это повышение немного скажется на обнищании народа. Это не так. Если у ракеты с полезной нагрузкой в 3 процента снизить силу тяги всего лишь на 3 процента, то она не выведет на орбиту  эту полезную нагрузку вообще. Человек здесь подобен машине – лишь меньшую часть потребляемой энергии он может потратить на прямое производство. Если народ обнищает на 10 %, то государство – значительно больше, что приведёт к растущей волне обнищания. И эта волна на нас уже накатилась. Вчера меня предупредили о вероятном закрытии   нашего клуба и некоторых других клубов города.

Но какова моральная сторона вопроса!!

Какова надежда на ясность в решении внутренних и внешних  проблем при такой совести?!

Несомненно, одной из причин такого кризиса мысли является плохая экологическая обстановка в городах, где проживают и заседают наши  монстры экономики, чиновники и их активные избиратели. И мы пытались им помочь, ведя посильный поиск новых чистых энергоносителей. Но вместо помощи  нас начисто обобрали. Они и о своих детях заботятся однобоко – их ждёт тяжёлое наследство.

Они порой хвастают своими познаниями  - это так, но это, чаще всего, лишь знание экономики своего кармана. Другие же прямо высказывают философию Белого Клыка в молодости: «Либо всех грызи – либо лежи в грязи». По телевизору они этого не говорят. Но хищная сущность выдаёт себя при всём нашем старании не видеть её. Они не дают достойного примера.

Но есть и такие, кто прямо и ожесточённо заявляет, что готов утопить интеллигенцию в её собственной крови. Утопить за то, что она выражает разумный протест против невежества, которое ведёт к разделению общества, к его убогости, к ослаблению власти руководства, к ситуации, когда небольшой просчёт правительства воспринимается обществом болезненно и с бурным возмущением. Подобное заявление было высказано видным спикером Госдумы с замашками Адольфа и Наполеона. Всем им неведомо, что не менее известный Александр Македонский уже давно пришёл к выводу, что победить мир можно только любовью. И для любви нужны знания.

Когда кто-то искренне и весьма талантливо поёт  песню о боли России – они не слышат её или не хотят слышать. Это было совсем недавно в Москве.

Не могу не привесть хотя бы несколько строчек:

 "Душу сбитую утратами да тратами,
   Душу стёртую перекатами -
   Если до крови лоскут истончал -
   Залатаю золотыми я заплатами,
   Чтобы чаще Господь замечал".

Они говорят, что умеют зарабатывать деньги. Мы же считаем, что они умеют их делать.  Знаем многих, кто хорошо работает, но ничего не имеет.

Мы не против богатства, мы против хамства в стремлении к нему, против его неразумного употребления.

Мы хотели бы видеть во всех стремление к осмыслению своего проживания на Земле. И здесь мне вспоминается сосновый куст, что рос на обочине дороги в пыли и мазутной гари, который в давние времена лучше человека объяснил мне свою суть.

И всё чаще помнятся слова нашего Ломоносова: «Тяжко в России насаждать науки». И мы с нетерпением ждём много лет, когда его дух  и дух Петра Великого, просвещённый веками, воспрянет и своим могучим дуэтом, «не щадя живота своего», воздаст должное.

В литературе и, особенно, в современном кино тоже мало вдохновляющих примеров. Тем более, весьма благодарны создателям фильма о Ломоносове (режиссёр Александр Прошкин). Колоссальные отзывы на этот фильм свидетельствуют, что этот дух жив и поныне.

Великолепна книга Магдалины Сизовой «Михайло Ломоносов» (изд. Молодая гвардия, 1954 г.).

Спасибо Марине Нееловой за роль Эстер, хотя главным героем там, кажется, был сыщик, преследовавший её. Последний свой махолёт мы назвали «Азазель». Так не хватает этого решительного и человечного образа (вместе с его единомышленниками), не вникая в то, кто послужил  Б. Акунину прототипом героини.

В реальной жизни много сил и души отдала детям и педагогам директор республиканской станции юных техников (г. Ижевск) Галина Лузенинова. Один орнитоптер мы назвали «Лузениана». Это пример другого чиновника, каких ждём, на которых надеемся.

Выражаю благодарность всем своим кружковцам за участие в сотворении махокрылов и эфироидов, за светлую веру в наше дело, в том числе:

Володе Проскурину, Анатолию Седых, Юрию Широбокову, Сергею Пономарёву, Жоре Кирьянову, Михаилу Петрову, Володе Петрову, Игорю Курсакову, Юрию и Роману Жуйковым, Андрею Соколову, Олегу Браточенко, Андрею Знатнову, Сергею Широбокову, Андрею Крылову, Сергею Петухову, Игорю Смолянскому, Алексею Стерхову, Алексею Глазырину, Анатолию Лапину, Сергею Веденскому, Андрею Репину, Николаю Буркову, Алексею Вольхину, Андрею Смольникову, Андрею Артемьеву, Андрею Топорову, Флюру Сабитову, Володе Варламову, Виктору Зотину, Виктору Чепурных, Алексею Жданову, Алексею Бездомникову, Александру Корякину, Алексею Коробейникову, Алексею Хворенкову, Алексею Ложкину, Антону Попову, Вячеславу Белоногову, Андрею Краснопёрову, Артёму Ложкину, Ивану и Алексею Кубельник, Ивану Суслову, Юрию Белому, Эдуарду Лопатину!

Выражаем признательность тем, кто помогал нам и содействовал: родителям кружковцев, нашим родственникам, специалистам машзавода и его профкому, друзьям, администрации, коллегам, журналистам, библиотекарям, водителям!

Благодарю! Владимира Крылова, который на протяжении десятилетий отслеживал работу кружка с фото, кино и видеокамерами, участвовал в испытаниях, хотя и не является сотрудником нашего клуба. Он имеет много кинозаписей нашей работы и некоторых испытаний аппаратов, сотни фотографий и цветных слайдов.

Благодарю Надежду Топорову! за многолетнее обеспечение клубной работы и участие в испытаниях.

Благодарю Юрия Белого и его родителей! За помощь в проведении экспериментов.  Их стараниям обязаны (данная и предыдущая) наши публикации.

Спасибо Якову Козлову! Как художнику и как участнику опасного эксперимента.

Спасибо Василию Златьеву! За активное участие в оформлении данной публикации.

Нам приходят письма по электронной почте. Они очень радуют! Но у нас давно сняли телефон, нет прямой связи с интернетом, нет средств – поэтому много чего нет: профессиональных помощников, своей видеокамеры (следовательно, нет видеозаписей  многих экспериментов), времени.… Но Ваши письма были всегда со мной, и тогда, когда писал данный трактат.

Хотелось бы оплачивать труд некоторых кружковцев. Они заслуживают этого, тем более, что способные и трудолюбивые часто встречаются среди бедных, очень нуждающихся. В июле прошлого года такое произошло – кружковцы получили за месяц работы над махолётом по 450 рублей (16 долларов). Эффект, конечно, положителен, но единичен.

В продаже отсутствуют наборы деталей для постройки летающих моделей. Раньше их можно было купить, можно было выписать по «Посылторгу». Школьники нуждаются в них.

Мы отработали  схематическую модель планера «Звёздочка» (каркас – из деревянных реек), резиномоторный вертолётик (из лёгкого пенопласта), отрабатываем серийный вариант модели махолёта.

Предлагаем для производства наборов или готовых изделий.

Предлагаем также принять участие в создании большого лёгкого махолёта с небольшой скоростью отрыва (~7 м/сек), что, предположительно, упростит испытания в наших условиях. Крылья будут махать полностью за счёт энергии воздуха.

Конечно, мы будем рады сотрудничеству и по другим направлениям. Например, разработка опытного эфирного движителя или двигателя. 

*            *           *

«Мир – бездна бездн. И каждый атом в нём
Проникнут богом – жизнью, красотою.
Живя и умирая, мы живём
Единою всемирною душою»

 

Иван Бунин

 

  В. Топоров,  2004 г.

Список основной литературы

 

1.  Г. В. Смирнов, «Рождённые вихрем», Москва., Знание, 1982.

2.  Г. С. Васильев, «Основы полёта моделей с машущими крыльями», Москва, Оборонгиз,                      1953.

3.  М. К. Тихонравов, «Полёт птиц и машины с машущими крыльями», Москва, Главная      редакция авиационной литературы, 1937.

4.  Г. С. Шестакова, «Строение крыльев и механика полёта птицы», М, Наука, 1971.

5.  В. В Голубев, «Лекции по теории крыла», М - Л, 1949.

6.  В.В.Голубев, «Исследование по теории машущего крыла», МГУ, 1949.

7.  Д. Лайтхил, «Аэродинамические аспекты полёта животных», Англия,

                          Кембриджский университет, 1975.

8.   Альманах о легкомоторной авиации «Аэромастер», Новосибирск, 1998-2003.

9.   В.М.Топоров. «Теория орнитоптера», Воткинск, КЮТ, 1983.

10. В.М.Топоров «К тайнам машущего полёта», 1990.

11. К.Уэлти, «Птицы», пер. с англ., М., «Мир», 1983.

12.  К1аus Wunderlich, “Natur als Konstruktor”, Edition Leipzig, 1976.

13.  Е.Д.Сорокодум, «Исследование течений, генерируемых колеблющимися перьями

                                     голубя», Таганрогский        радиоинститут, 1982.

14.  Е.Д.Сорокодум, «Распределение массы, моментов инерции и площадей ...пера голубя»

15.  А. Вracke, «Орнитоптеры», пер. с фр., Москва, типография Сомовой, 1910.

16.  Е.С.Джеймс, «Заметки о машущем полёте с продольным движением крыла»,

                                США,военно-морской центр, Бетесда, 1979.

17.  У.М.Норберг, «Элементы структуры крыла рукокрылых», пер. с анл., г. Гетеборг,

                                 Швеция, 1972.

18.  W. ВirnЬаum, «Задача о машущем крыле в двухмерной постановке», пер. с нем.,

                                 Москва, 1967. Решение приложено к явлению флаттера.

19.  Э.П.Гребешов, О.А.Сагоян, «Гидродинамические характеристики колеблющегося

                                                           крыла...», Москва,ЦАГИ, -1975.

20.  Я.Фитек, Негер Джон, «Экспериментальное изучение подъёмной силы и тяги

                  машущего крыла», Канада, Tоронто, институт аэрокосмических исследований и 

                   компания «Пратт энд Уитни», пер. с англ., М., 1981.

21.  А.А.Пирогов, «ОВЕЛА - новый способ полёта», доклад на СЛА-87, Москва.

22.  В.А.Свидерский, «Полёт насекомого», Москва, «Наука», 1980.

23.  В.А.Киселёв, «Машущий полёт - техническая реальность», ж. «Изобретатель-

                                 рационализатор», 1982, № 10.

24.  А.А.Борин, «Машущий полёт - мифы и перспективы», ж. М.-К.,1983, №11.

25   В.П.Казневский, «Аэродинамика в природе и технике», М., «Просвещение», 1985.

26.  А.К.Бродский, « Механика полёта насекомых», Ленинградский университет, 1988.

27.  О.М.Бочарова-Месснер, «Рельеф поверхности крыльев насекомых», доклад АН СССР,

                                                    1978.

28.  Ацума, «Механика полёта стрекоз», Япония, -1980.

29.  А.А.Атланов, «Махолёт: от идеи до машины», ж. ТМ, 1978, №9.

30.  Н.Вожегов, «Эффект машущего крыла», ж. ЮТ, 1975, №6.

31.  А.К.Мартынов, «Экспериментальная аэродинамика», М., Оборонгиз, 1950.

32.  Н.Я.Фабрикант, «Аэродинамика», М., «Наука», 1964.

33.  А. Болонкин, «Теория полёта летающих моделей», М., ДОСААФ,1962.

34.  С.Т.Кашафутдинов, В.Н.Лушин, «Атлас аэродинамических характеристик

                                                               крыловых профилей», Сиб. НИА, 1994.

35. Е.Д. Сорокодум, «Кризис науки, техники и человеческих возможностей», E – mail:

                                     e40dum@dol. ru        http://vortex.viptop.ru

36. В.М. Топоров, «Воздух и эфир – источники живой силы», Воткинск, СЮТ, 1994.

37.  С.А.Горбатенко и др., «Механика полёта», М., «Машиностроение», 1969.

38.  В. А. Ацюковский, «Общая эфиродинамика», Москва, «Энергоатомиздат», 1990.

39.  В.А.Ацюковский, «Материализм и релятивизм», М., «Энергоатомиздат»1992.

                                     Критика методологии современной теоретической физики.

40.  В.А.Ацюковский, «Эфирный ветер», М., «Энергоатомиздат», 1993.

41.  В.А.Ацюковский, «12 экспериментов по эфиродинамике», г. Жуковский, 2003.

42.  Ю.М.Галаев,  «Эфирный  ветер»,  Эксперимент  в диапазоне радиоволн,

                                ЗАО «Петит», 2000.

43.  П.Даффет - Смит, «Практическая астрономия...», пер. с англ., М., «Мир», 1982.

44.  В.В.Шевченко, «Луна и её наблюдения», М., «Наука», 1983.

45.  А. А.Михайлов, «Земля и её вращение», М., «Наука», 1984.

46.  Л.Г.Лойцянский, А. И. Лурье, «Курс теоретической механики», Государственное

                                    издательство технико-теоретической литературы, М., 1954, Том 1-2.

47.  А.И.Лурье, «Аналитическая механика», изд. физико - мат. лит., М., 1961.

48.  Р.Ф.Аппазов, «Баллистика управляемых ракет дальнего действия», М.«Наука», 1966.

49.  Д.В.Сивухин, «Общий курс физики», М., «Наука», 1989.

50.  Н.П.Грушинский, «В мире сил тяготения», М., «Недра», 1985.

51.  У.Каспер, «Тяготение загадочное и привычное», ГДР.

52.  Михал, «Вечный двигатель вчера и сегодня», М., «Мир», 1984.

53.  С.Херрик, «Астродинамика», пер. с англ., М., «Мир», 1978, 3 тома.

54.  С.Б.Пикельнер, «Физика космоса», М., «Советская энциклопедия», 1976.

55.  В.Н.Комаров, Б.Н.Пановкин, «Занимательная астрофизика», М., «Наука», 1984.

56.  И.С.Шкловский, «Вселенная, жизнь, разум», М., «Наука», 1987.

57.  Б.М.Яворский, «Справочник по физике», М., «Наука», 1977.

58.  Н.И.Кошкин, М.Г.Ширкевич, «Справочник по элементарной физике», М., «Наука».

59.  Г.С.Ландсберг, «Элементарный учебник физики», 3 тома, М., «Наука», 1972.

60.  А.А. Яблонский, «Курс теоретической механики», М., «Высшая школа», 1971.

61.  И.М.Воронков, «Курс теоретической механики», М.,»Наука», 1964.

62.  Я.И.Перельман, «Занимательная физика», Екатеринбург, «Тезис», 1994.

63.  П.П.Пекарский, «Наука и литература при Петре 1», Санкт-Петербург, 1862, том 1.

64.  В.Н.Толчин, «Основные начала механики в материалистическом понимании»,

                               Пермь, 1968.

65.  В.Н.Толчин, «Инерцоид», Пермское книжное издательство, 1977.

66.  В.М.Топоров, «Третья производная в механике», Воткинск, 1991.

67.  В.М.Топоров, «Земные и небесные неравенства», Воткинск, СЮТ,1993.

68.  В.А.Бронштэн, «Как движется Луна», М., «Наука», 1990.

69.  А.Т.Григорьян, «Механика от античности до наших дней», М., «Наука», 1974.

70.  Ю.Марков, «Курс на Марс», М., «Машиностроение», 1989.

71.  «Астрономический ежегодник», «Астрономический календарь», Санкт-Петербург,

         1955 -2004.

72.  Н.П.Ерпылёв, «Энциклопедический словарь юного астронома», М. «Педаг.», 1980.

73.  В.К.Милюков, М.У.Сагитов, «Гравитационная постоянная в астрономии»,

                                                          М.,«Знание», 1985.

74.  Б.А.Воронцов-Вельяминов, «Астрономия», М., «Просвещение», 1991.

75.  Д. Ренделс, П. Хоу, «Тайны НЛО», М., «Вече», 2000.

76.  Д.Е. Охоцимский, «Основы механики космического полёта», М.., «Наука», 1990.

77.  Журнал «Техника», 1991/3, Инженер-изобретатель, Москва, «Знание».

78.  П.Д. Остапенко, «Вопросы о погоде», Ленинград, «Гидрометеоиздат», 1986.

79.  П.С. Кудрявцев, «Исаак Ньютон», Москва, «Просвещение», 1963.

80. М.В. Ломоносов, «О тяжести тел и извечности первичного движения», полное собрание

                                     сочинений, т.2, М., АН СССР, 1951.

«Никитка – первый русский летун».  Художник Александр Дейнека, 1940 г.

 

 

 

«Человек – не птица, крыльев не имать, аже  щё приставит себе крылья деревянные – противу естества творит. То не божье дело, то от  нечистой силы. Отрубить выдумщику голову!»       

из указа царя Ивана Грозного.

 

 

  Ключёвское алабино

 

 

 

 

 

Механика живого неба.

Махокрылы и эфироиды в экспериментах.

На лицевой стороне обложки вверху  - фотоснимок с полотна «Мечта»,

Художник Яков Козлов, 1992 г. 

В работе использованы фотографии Владимира Крылова, Анатолия Седых, Юрия Белого, автора и др.

Рисунки  – автора.

Компьютерное обеспечение – Юрия Белого.

Перевод и обработка рисунков - Василия Златьева.

 

Размещено на сайте 16.09.2012

Статьи других авторов

На главную