
Аннотация: Инерцоид Толчина продолжает вызывать к себе интерес со стороны как научных работников, так и со стороны любителей. Из учёных наиболее известен Г.И.Шипов, который попытался применить к инерцоиду Толчина свою теорию 4D-гироскопов. Целью статьи не является полемика с Г.И.Шиповым. Ибо Г.И.Шипов в своих работах решает глобальные вопросы. У меня же задача попроще. Сделана, опираясь на теорию Эфира русского дилетанта без формул, попытка показать, что поведение инерцоида Толчина можно подробно описать, приняв наличие центробежных сил при вращении грузов либо с переменной частотой вращения, либо с переменной длинной прутов, на концах которых располагаются грузы. Центробежные силы — это силы внешние по отношению к инерцоиду, которые возникают в тех случаях, когда тело движется по криволинейной траектории, и являются результатом взаимодействия тела с окружающим Эфиром. Центробежная сила — это аналог подъёмной силы в аэродинамике. Во время проведения экспериментов в программе «Живая физика» были обнаружены раннее неизвестные мне механические феномены, которые требуют по новому посмотреть на инерцоид Толчина или возможные недостатки программы «Живая физика».
Ключевые слова: Эфир, давление Эфира, градиент эфирного давления, уравнение Бернулли, вещество, вихри и потоки Эфира, эфирный вакуум, энергия, вечный двигатель, вечное движение, гравитация, масса, инерция, энергия, безопорное (эфироопорное) движение, вращение, центробежная сила, транспортное средство на эфироопорной тяге, инерцоид Толчина, силы инерции как источник поступательного движения, гироскопический эффект.
/*/
Центробежная сила является настоящим подарком Природы и Эфира человечеству. Значение центробежной силы еще не понято современной официальной наукой в достаточной степени. Из числа официальных академиков 60-70% не признают центробежную силу за реальную, а смотрят на неё как вспомогательный инструмент, позволяющий неинерциальную систему превратить в инерциальную. Как и не понято в полной мере значение такой формы движения как вращение. Именно вращение является наиболее часто встречаемой в Природе формой движения. Поэтому СТО и ОТО Альберта Эйнштейна не могут считаться теориями, претендующими на роль самых главных теорий. Ибо с позиции СТО и ОТО все системы инерциальны. Когда же приходится исследовать процессы в реальной системе, где вещество вращается, то СТО и ОТО не могут это адекватно отобразить.
Это ведёт к тому, что до сих пор мы не ездим, не плаваем и не летаем с использованием эфирных технологий, используем энергию, получаемую при сжигании углеводородов. По сути, живём в реальном Аду. Даже главам государств мастистые академики запудрили мозги. Вот недавно Путин В.В. на весь мир заявил, что России нет смысла развивать альтернативные технологии получения энергии, мол, в России много газа и Россия будет развивать газовые технологии. Дожили!! Действительно, социализм России не грозит… Или это просто профессиональный трёп разведчика?
Между тем, теория Эфира русского дилетанта без формул позволяет без напряга и самым естественным образом объяснить многие известные физике факты и законы, как касающиеся прямолинейного, так и криволинейного движения, в котором центробежные силы играют важную роль. Это касается как хорошо известного гироскопического эффекта, так и такой, часто забываемой, силы Кориолиса или инерции маховика при попытке остановить его. Инерция маховика (гироскопа), сила Кориолиса и центробежная сила, уверен, станут в ближайшие десятилетия важными источниками энергии и движителями для всего человечества, позволят создать безтопливный, безкрылый, безколёсный транспорт для перемещения по земле, воздуху и под водой. Но, самое главное, человечество на таком транспорте сможет выйти в Космос и начать осваивать планеты и их спутники в солнечной системе.
Особенно радует то, что многие факты, которые не находили объяснения со стороны мастистых официальных академиков, удается понять на основе всем хорошо известных законов физики и механики. Но только при условии, что при этом обязательно принимается в расчет центробежные силы, которые формируются при движении тела по криволинейной траектории, и, в частности, в любом инерцоиде. Вопрос только в том, как центробежные силы проявляются, напрямую или опосредованно.
Первый инерцоид в СССР, и, похоже, в мире, сконструировал в 1936 году инженер В.Н. Толчин. На рис.1. показан один из инерцоидов Толчина, которые он использовал в своих опытах. Принцип действия очень простой - два грузика вращаются синхронно, в разных направлениях, что компенсирует крутящий момент.

Рис. 1. Инерциоид Толчина
Злые языки говорят, что Толчин со своими инерцоидами ломился в открытые двери, что еще в 1930 году некий изобретатель в СССР предложил систему на маховиках с дебалансами для создания инерционной тяги и получил на неё авторское свидетельство. Лично я заслугой Толчина считаю, что он не только изобрёл простой инерцоидный движитель, но и предложил на базе простых моделей минимум три варианта использования их в транспорте и в энергетике. А заодно поставил всю АН СССР буквально на уши. Он смог сделать, а академики не смогли.
В его конструкциях использовался простой способ разгона грузов по окружности. Условно и с достаточной точностью можно считать, что каждый груз вначале в диапазоне от 0 до 30 градусов разгоняется, а, после того как грузы достигнут 150 градусов, начинается их торможение до 180 градусов. Далее грузы движутся по инерции к началу траектории. Это приводит к тому, что в той части траектории, где скорость перемещения грузов больше, центробежная сила оказывается больше, поэтому в ту сторону формируется центробежная безопорная тяга, которая и перемещает инерцоид. Но это так кажется, так как изменение угла поворота груза изменяется во времени неравномерно. А это приводит к тому, что с учётом данного фактора итоговая центробежная сила за один оборот грузов оказывается равной нулю.
Заслуги Толчина В.Н. огромны. Но его роль в создании новых видов транспорта и энергетики так и не получила должной оценки со стороны официальной науки. Видимо, потому, что Толчин В.Н. отказался разделить славу с «мастистыми» учеными», а те в отместку окрестили его сумасшедшим и наложили запрет выдавать патенты на изобретения, если они хотя бы отдаленно походили на инерцоиды. Тем более, изобретатели инерцоидов сами себя подставляли под критику хотя тем, что не могли доказать свою правоту ученым на том языке, на котором привыкли разговаривать ученые. А сами ученые также показали себя во всей красе, оказавшись не способными говорить на языке изобретателей. Одни не смогли, а другие не захотели. Как в любой революции.
Сам Толчин немного подпортил себе и своим последователям возможность доказать свою правоту тем, что категорически отрицал влияние центробежных сил на поведение своего инерцоида. Может быть он прав, хотя бы частично. И двигали его инерцоиды совсем не центробежные силы. Это привело к тому, что даже в серьёзных научных работах про инерцоиды на центробежные силы внимание не обращается, а говорится про некие кручения и вращения окружающего пространства-времени.
Лично я считаю, что инерцоиды в первую очередь перемещаются в пространстве благодаря центробежным силам. Точнее центробежные силы надо в первую очередь использовать в инерционных движителях. Хотя и обычная инерция, с которой может быть связано смещение центра масс при вращении грузов, также может влиять на поведение инерцоида, но её роль значительно уступает роли центробежных сил, особенно при увеличении угловой скорости вращения грузов. Скорость перемещения центра тяжести пропорциональна частоте вращения, а центробежная сила - квадрату частоты вращения. Разница есть, и эта разница при высокой частоте вращения огромная.
Также надо при изучении инерцоидов учитывать гироскопические эффекты, что, судя по имеющимся у меня данным, практически никто не делает.
Потом, центробежные силы центр масс инерцоида смещают в одном направлении, а силы, связанные с перемещением масс вдоль «горизонтальной» оси Х, имеют строго периодический характер и поэтому накладывают на прерывистое перемещение инерцоида под влиянием центробежных сил некий осциллирующий фон.
Например, у Толчина масса эксцентриков (грузов) была больше массы остальной части инерцоидов. Поэтому движение таких конструкций больше напоминало движение устройств, в которых для перемещения по поверхностям использовали линейные вибраторы. Такие устройства могли перемещаться только по тем поверхностям, от которых они могут отталкиваться благодаря трению. Например, Нурбей Гулия, создавший супермаховик и несколько вариантов «кузнечиков», превратился в яростного критика изобретателей инерцоидов. Но критику он вел методом подмена понятий, абсолютно не учитывая, что для инерцоида важное значение имеет центробежные силы, а не просто линейные перемещения одних частей инерцоида относительно других.
Чтобы раз и навсегда прекратить споры о необходимости изменения положения центра масс, надо договориться о необходимых условиях (ограничениях, принципах) при конструировании инерцоидов. Ничто не мешает в конструкции инерцоида сразу на этапе проектирования предусмотреть два блока. Один будет создавать тягу в определенном направлении, например, генерируя её с помощью центробежной силы, но при этом создавая в качестве побочного результата изменение положения центра масс. А другой блок будет нарушенное положение центра масс восстанавливать, но уже без применения вращения и центробежных сил. Кроме того, надо, чтобы общая масса инерцоида была в несколько раз больше массы грузов. Это позволит за счёт инерции общей массы снизить такой эффект как продольная вибрация при движении инерцоида. Также стоит обязательно предусмотреть в конструкции инерцоида использование не двух грузов, а, вообще, любого чётного количества грузов. Это позволит во много раз нарастить силу тяги и упростить механизм компенсации сдвига центра масс инерцоида с помощью невращающейся массы. В покое такая масса будет находиться под осью «маховика» с грузами. А когда «маховик» с грузами начнет вращаться, создавая центробежную силу, то, в случае, если тяга будет создаваться за счёт смещения грузов, эта масса будет немного смещаться «назад», восстанавливая положение центра масс всего инерцоида. Если тяга будет создаваться исключительно за счет изменения частоты вращения «маховика» с грузами, то в компенсации положения центра масс необходимости не будет.
Исследованиями инерцоидов после Толчина некоторые изобретатели и ученые занимались, по сути, подпольно. Среди них следует особо выделить А.Е. Акимова и Г.И.Шипова. Эти ученые попытались раскрыть особенности движения инерцоидов с позиций «торсионной механики» и 4D-гироскопа.
Г.И. Шипов разработал свою теорию торсионного поля и 4D-гироскопа, которую он позиционировал как развитие ОТО А.Эйнштейна, но только ввел в неё такие понятия как вращение и кручение пространства. Думаю, будучи дилетантом, что это является ошибкой Г.И. Шипова, так как скручивать надо не пространство, а материю, которая находится в нём. Точнее, даже не скручивать, а закручивать в разные варианты вихрей, потоков и волн. Эфир, как среда, это реализовывать позволяет.
С одной стороны, осуждать и особо критиковать Г.И.Шипова я не имею права, хотя бы потому, что мне до Шипова далеко. С другой стороны, в то время только будучи сторонником СТО и ОТО, можно было рассчитывать на возможность работать в каком-либо научном учреждении СССР. Г.И.Шипов в своих воспоминаниях живо описал, как вели себя многие так называемые ученые, как они рвали на куски его диссертацию, как, пользуясь телефонным правом, не давали ему не то, что защитить кандидатскую диссертацию, но и даже работать, например, в МГУ. Думаю, что Шипова подвергли гонениям уже за то, что он посмел усомниться в идеях А.Эйнштейна и имел «наглость» предложить свою теорию, пусть даже очень похожую на ОТО, и использующую близкий математический язык.
В принципе такие хамы, с которыми встречался на своем жизненном пути Шипов, встречаются не только в науке. Современные политики это явно демонстрируют чуть ли не каждый день. Город Глупов в натуре. Губернаторы из медведей то и дело чижиков съедают. Видимо, это одна из особенностей нашего общества, наш исторический и социальный недостаток, от которого мы не может избавиться уже в течение нескольких столетий, если не тысячелетий. Поэтому мы все, за редким исключением, так плохо живём. Управление плохое. Или власть работает не на того парня.
А.Е. Акимов больше работал как практик, исследуя воздействие вихревых эфирных полей на течение процессов в веществе и живых организмах. И в этом направлении ему удалось добиться определённых успехов. Хотя это не помешало некоторым академикам РАН обозвать как А.Е.Акимова, так и Г.И. Шипова лжеучеными. Видимо, тем, кто занимается в РАН борьбой с «лжеучеными», просто делать нечего. На версту пахнет национальным и государственным предательством. Видимо, члены комиссии по борьбе с лженаукой получили от кого-то довольно могущественного задание уничтожать в России настоящих учёных. И ведь последних не только шельмуют, но и убивают. Многих убили...
Не зря ведь из школьных учебников по физике исключили изучение центробежной силы. Есть, мол, центростремительная сила в качестве первичной силы. Короче, виртуальное и вторичное превратили в реальное и первичное. А центробежную силу, благодаря которой спортивные молотобойцы бросают свои молоты, предали забвению. И это уже не смешно.
Когда коту делать нечего… Поэтому они от нечего делать реализуют древний завет Моисея, что разного рода колдунов и магов, как и священников других богов, противников Яхве, следует убивать камнями. Это я не от себя говорю, это в Ветхом завете написано. Что написано пером, не вырубишь и топором. Да, недалеко мы продвинулись в развитии по сравнению с ветхими иудеями. Времена, вроде бы другие, а методы борьбы с иными идеологиями и взглядами остались прежними - изгнание из сообщества и забвение, вплоть до физического уничтожения. Камнями их, камнями…
Забыли учёные, что Давид убил Голиафа с помощью центробежной силы (камнем, выпущенным из пращи). По этому случаю надо бы центробежную силу назвать святой силой, а оно вон как получается. Учёные против Бога и Природы идут.
Но Г.И. Шипов продолжал бороться, и в 1981 году, работая в фирме Туполева, изготовил два инерцоида по схеме Толчина. Затем последовало успешное испытание инерцоидов в МГУ на платформе на воздушной подушке. Когда Шипов, желая усовершенствовать инерцоид Толчина, подал заявку на изобретение в 1991 году, то получил отказ со ссылкой на некое секретное Постановление, запрещающее в СССР рассматривать заявки, если они касались инерцоидов. Получается, что и Политбюро ЦК КПСС воевало со своим народом и истинными учёными.
В АН СССР и РАН даже изобрели формулировку – «движение системы за счет внутренних сил». Считаю, что данная формулировка должна быть изменена на другую – «движение системы за счет взаимодействия системы окружающей средой (Эфиром)». Но пока РАН не признает Эфир в качестве окружающей среды, надеяться на это нет смысла.
Несмотря на отказы со стороны Роспатента Шипов продолжал свои работы с инерцоидами. Экспериментально, эффект Толчина и работоспособность его инерциоида были неоднократно подтверждены не только в результате самостоятельной работы Шипова, но также, в ходе совместных экспериментов с американскими учеными.
В 2000 г. Шипов Г.И. исследовал инерциоиды в лаборатории, которую специально создали на деньги спонсоров в Таиланде. В 2002 году, НИИ Космических систем имени Хруничева он начал серьезно заниматься темой инерционных движителей, что привело к созданию новой системы корректировки орбиты спутника «Юбилейный».
К сожалению, сам эксперимент на спутнике многие признают неудачным. Думаю, не исключается самая обыкновенная диверсия. Шипову дали возможность разработать инерционный движитель, позволили его установить на спутник, но вот должным образом работу этого двигателя не организовали. А информацию о движителе, скорее всего, давно передали американцам, как это было сделано со многими прорывными открытия и изобретениями российских ученых. В современных условиях сделать это не составляет труда. Продается и покупается всё, правда не все еще оскотинились. Если уж можно фальсифицировать итоги выборов, то подделать результаты физического эксперимента раз плюнуть.
Практика жизни показывает, что между диктатурой пролетариата и идеологией СТО и ОТО нет принципиальной разницы. Диктатура она и есть диктатура. Любая диктатура — это геноцид. Раньше у нас была диктатура пролетариата, сегодня диктатура либерала. Итог — массовая гибель людей, где от пули, где от голода и социального стресса. Хрен редьки не слаще. Видимо, есть категория людей, которые без диктатуры над окружающими не могут нормально жить. Такое у них ущербное сознание.
Один из инерцоидов, созданных Шиповым Г.И., показан на рис. 2.

Рис.2. Инерцоид Шипова Г.И. Рисунок взять из работы Шипова.
В принципе этот инерцоид не отличался от инерцоида Толчина, только управление вращением масс (эксцентриков), их ускорением и торможением занималась компьютерная программа, которая одновременно фиксировала параметры движения этого инерцоида.
Шипову экспериментально удалось доказать, что инерцоид действительно перемещается в пространстве не только по рельсам, но и способен перемещать модели судов, мог перемещаться по нити, по смазанной маслом поверхности, на воздушной подушке. Поэтому для окончательных выводов было решено вывести инерцоид Шипова в космос на спутнике «Юбилейный», чтобы уже в невесомости проверить работоспособность инерцоида. Но что-то там пошло не так. И, похоже, это происки врагов, которым очень не хочется, чтобы у России появились инерционные движители и двигатели. А может быть военные засекретили, чтобы враги не воспользовались.
Глядя на инерцоид Толчина или Шипова, столь простой аппарат, на модернизацию которого не нужно тратить миллиарды долларов, удивляешься косности и невежеству тех, кто занимает властные посты в России. Ведь это так очевидно, что инерцоиды следует изучать, строить и использовать как источники силы и механизмы по выработке океанов энергии! В таком аппарате работает Эфир, как он же работает в любом магните. Но лучше российский чиновник приберет к рукам несколько сотен миллионов долларов для строительства личной дачи в Испании, чем выделит изобретателю, например Шипову Г.И, жалкий миллион. И все потому, что Шипов старается сделать доброе дело для всех, а чиновником, за редким исключением, управляет его собственное брюхо и голова, набитые разным либеральным хламом.
/*/
Попробуем вначале описать поведение инерцоида под действием центробежных сил, создаваемых массами m при вращении вокруг оси O1. Примем в первом приближении, что центр масс инерцоида (M+2*m) при вращении масс m практически не изменятся. Если кого-то это не устроит, то пример, что масса M состоит из двух частей, на одной из которых стоит ось для масс m, а другая половина связана с первой таким образом, что она при вращении масс m смещается вдоль оси Х так, чтобы общий центр масс практически не смещался.
На рис.3. показано взаимодействие масс M и двух m при вращении последних вокруг оси О1.
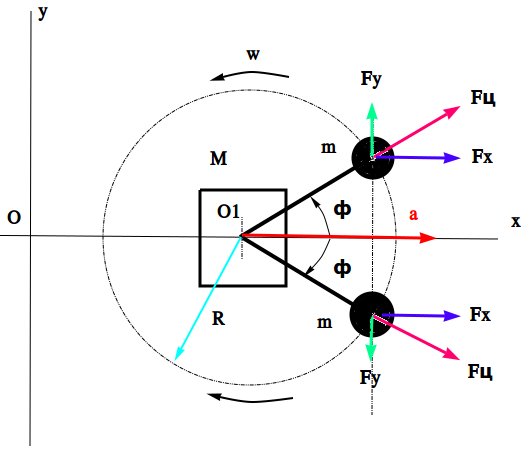
Рис.3.
Вращающиеся обе массы m порождают центробежные силы, проекции которых на ось X создют силу F, под действием которой инерцоид (M+2*m) приобретает ускорение a. Решая эти уравнения относительно ускорения a, получаем, что
a =G*cos(ф) (1)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
То есть, мы пока предполагаем, что грузы m вращаются в разных направлениях с постоянной угловой частотой w вокруг оси О1. Зная ускорение инерцоида a, можно легко найти скорость V и путь S.
В формуле (1) мы пока предполагаем, что коэффициент K есть константа, так как предполагается, что M, m, w, R не изменяются.
Если мы проинтегрируем уравнение (1), то получим скорость инерцоида в зависимости от накрученных на ось О1 оборотов в радианах. Если проинтегрируем полученную скорость по ф, то получим пройденный путь в зависимости от накрученных на ось О1 оборотов в радианах. Если частота вращения грузов m постоянная, то найти скорость и путь в зависимости от времени, ничего не стоит. А вот если частота вращения грузов m вокруг оси О1, будет переменной, как в инерцоиде Толчина, то привести развитую скорость и пройденный путь к пройденному времени, будет сложно. Но в первом приближении можно пользоваться некой средней частотой вращения.
Используя уравнение (1) для вычисления скорости и пути, мы получим, что в ответ на гармоничность ускорения, скорость и пройденный путь тоже будут изменяться по гармоническому закону. То есть центр масс изменяться не будет. А инерцоид будет вести себя как классический осциллятор. Если мы рассчитаем средние за период ускорение, скорость и путь, то получим круглые нули.
Чтобы инерцоид начал двигаться вдоль оси Х, необходимо ввести в систему асимметрию. Либо сделать частоту вращения зависящей от угла поворота ф масс m. Либо радиус R сделать зависимым от угла ф. Либо сделать зависимым от угла ф и то и другое. Можно попробовать менять массу m. Технически это возможно. Вопрос только в целесообразности такого решения.
Мне нравится решение использовать для формирования тяги в инерцоиде маховик, вращающийся вокруг двух осей с одинаковой угловой скоростью. В данной конструкции (рис.4) уже «стоят» два дебаланса, вращающихся в разных направлениях, которые вместе создают тягу вверх. Надо только от мотора набросить ремень на шкиф.
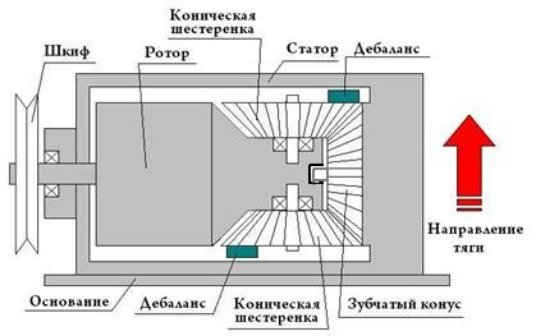
Рис.4.
В этом случае уравнение для ускорения центра масс инерцоида будет выглядеть так:
a =G*cos(ф)*cos(ф) (2)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
У данного, с виду простого, решения есть один недостаток. При высоких оборотах начинает проявлять норов сила Кориолиса, которая вначале изгибает шестерёнки восьмёркой, а при увеличении частоты их ломает. Но для получения точного математического решения такой вариант самый простой.
Вначале найдем среднее за оборот ускорение инерцоида. Интегрируя уравнение (2) по ф от 0 до 360 градусов, получим для а_ср = G/2. То есть среднее ускорение положительное и довольно значительное. Так что в качестве инерцоида моя конструкция вполне подходит, если бы не сила Кориолиса. Но в некоторых случаях, там где нет высоких частот вращения, такую конструкцию вполне можно использовать. Например, для носильщиков вокзалов. Им вполне достаточно облегчения веса поклажи раза в 2-3.
Интегрируя уравнение (2) по ф, получим для скорости:
V = G*(ф/2 + sin(2ф)/4) (3)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — суммарный угол ф грузов m.
Получаем, что скорость инерцоида с моим движком будет изменяться линейно-волнисто, постепенно нарастая с числом сделанных массами m оборотов вокруг оси О1.
Если мы теперь проинтегрируем уравнение (3), получим для пройденного пути S:
S = G*(ф*ф/4 - cos(2ф)/8) (4)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — суммарный угол ф грузов m.
Получаем, что пройденный путь инерцоида с моим движком будет изменяться квадратно-волнисто, постепенно нарастая с числом сделанных массами m оборотов вокруг оси О1.
Формулы (2), (3) и (4) полностью соответствуют законам механики, законам Ньютона для тел, двигающихся ускоренно под действием, пусть и пульсирующей, но положительной силы. А сама пульсирующая вдоль оси Х во времени сила является интегрированием постоянной центробежной силы, но меняющей своё направление по заданному конструкцией закону. Средняя за один оборот грузов m тяга равна половине центробежной силы. Так как в устройстве две шестерёнки с дебалансами, то сила тяги равна центробежной силе Fц.
Формулы (2), (3) и (4) получены с условием, что инерцоид не будет испытывать сопротивления среды и других тел. Но если сила сопротивления будет равна силе тяги, то инерцоид будет двигаться равномерно, с постоянной скоростью, как и положено ему по законам Ньютона.
Таким образом, ничего сверхъестественного в поведении инерцоида нет. Просто он своими вращающимися грузами m создает неравномерные потоки Эфира, а последние, создавая «поъёмную», центробежную силу, тянут весь инерцоид по направлению центробежной силы. Центробежная сила является внешней по отношению к инерцоиду силой. Это не фиктивная или виртуальная сила, это самая настоящая реальная сила, возникающая в результате взаимодействия вращающихся грузов m с окружающим Эфиром. И тот факт, что силы тяги велика, указывает на то, что Эфир - это плотная жидкость, либо сверхплотный, доведенный до жидкого состояния, газ, в котором иногда при снижении локального динамического давления появляются пузырьки того же Эфира в виде вращающихся нуклонов.
Для создания тяги можно использовать алгоритм Бережного А.Б. Вот его устройство (рис.5)

Рис.5. Инерцоид Бережного А.Б.
В этом устройстве два дебаланса (груза) по 50 г при вращении создают довольно заметную пульсирующую тягу, направленную в одном направлении. Когда грузы доходят до рамы, рама поворачивается на 180 градусов, в результате грузы постоянно вращаются по половине окружности над рамой. В принципе, раму можно повернуть так, чтобы тяга была направленна в нужном направлении.
Так как теперь грузы всегда находятся «впереди» оси О1, то вместо осциллятора получается инерцоид с положительной пульсирующей тягой. Так ведёт себя напряжение после преобразования в диодном мосту — был переменный ток, стал постоянным, но пульсирующим. Остается пульсирующую тягу направить в аккумулятор механической энергии, а оттуда использовать эту энергию уже для тяги постоянной. Или поставить в ряд сразу несколько таких инерцоидов, у которых грузы вращаются со сдвигом фаз. 3-4 таких инерцоида обеспечат плавный ход перемещаемого устройства.
Формулу (1) теперь мы изменим на такую:
a =G*abs(cos(ф)) (5)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
Эта формула уже просто так не интегрируется по ф. Ибо функция не гладкая. Поэтому решение можно найти либо численными методами, либо использовать функцию «Целая часть числа» Int(). Интуиция подсказывает, что скорость будет линейно-волнисто, а пройденный путь будет квадратно-волнисто зависеть от количества оборотов грузов m. Только теперь оборот будет составлять не 360 градусов, а только 180.
Но мы можем вычислить среднее ускорение a, что позволит узнать силу, которая будет воздействовать на транспортное средство (инерцоид). а_ср = 0,637*K. Это почти на 13% больше, чем в моём случае, где среднее ускорение равно a_ср = 0,5*K. Но разница не такая большая, чтобы посыпать голову пеплом.
С другой стороны алгоритм Бережного А.Б. можно реализовать не только чисто механически, но и с помощью гидравлики. Для этого надо иметь две емкости на диске на диаметрально противоположных сторонах. Одна из ёмкостей должна быть заполнена жидкостью или жидким металлом, а вторая ёмкость пустая. В этот диск должна быть встроена система удаления жидкости из ёмкости, если она окажется при вращении в «задней» части диска, и наполнения ёмкости, если она окажется в «передней» части диска. Тогда через каждые полоборота на «передней» части диска будет находиться емкость с жидкостью, а на «задней» части — пустая. Это будет соответствовать формуле (5). Технически, думаю, это реализовать можно. Только теперь на инерцоиде должно стоять два таких диска, вращающихся в разных направлениях, один по часовой, а другой против часовой стрелки.
Если на диске мы расположит парное число ёмкостей (4-6-8-10-12), то получим движитель, который будет создавать практически идеальную тягу. Технически реализовать можно, если хорошо подумать. Мне приходилось разрабатывать в уме подобные системы для гравитационных колёс. Гидравлика может тут помочь. Причём всё можно организовать по принципу теплового насоса. Насос будет перекачивать масло из одной ёмкости в другую, создавая в них разность давлений. Остальное будет осуществляться автоматически. Некоторые ёмкости будут сбрасывать масло в ёмкость с низким давлением, а другие, парные им, будут в нужном месте и в нужное время маслом автоматически наполняться. Дело техники и никакого мошенства.
Два варианта организации движения грузов в инерцоиде мы рассмотрели. И получили неплохие результаты. Причём при этом не пришлось прибегать к тому, что современная физика не знает. Инерцоид — это устройство, функционирование которого полностью соответствует законам физики. Силой, которая перемещает инерцоид в пространстве, является центробежная сила, которая является эфироопорной силой, полным аналогом подъёмной силы в аэродинамике.
Примерно 100 лет назад кое-кто из известных мировых физиков утверждал, что тела, плотность которых выше плотности воздуха, летать не могут. Да, статически летать в воздухе нельзя, а вот динамически можно. Птицы летают. Так что осталось убедить современных академиков, что можно летать, опираясь на Эфир. Но для этого их надо убедить, что Эфир существует. В случае чего мы просто подождём, пока не произойдёт смены поколений. Век тиранов не долог. Тирания, как правило, заканчивается со смертью тирана. Душа Робеспьера тому свидетель.
/*/
Теперь приступим к рассмотрению варианта организации движения грузов по алгоритму, который я называю алгоритмом Толчина. В этом случае усиление центробежной силы спереди и ослабление её сзади инерцоида осуществляется неравномерным вращением грузов. Когда грузы оказываются спереди, то частота вращения их увеличивается, когда сзади — уменьшается. Получается неравномерное вращение грузов, которое с одной стороны позволяет создать пульсирующую тягу с преобладанием её в правом направлении. Но с другой стороны усложняется расчёт важных характеристик инерцоида, неравномерность тяги вызывает недоверие в то, что такое устройство может быть движителем. Вот (рис.6) результат замеров движения реального инерцоида, у которого периоды ускорения и торможения происходят только в короткие интервалы времени. Видно, что инерцоид то движется вперёд, то пятится назад, траектория волнистая. Ездить на таком транспорте никто не захочет.
Но в любом случае алгоритм близкий к алгоритму Толчина рассмотреть и исследовать следует. Чтобы иметь о нём хоть какое-то представления. И к какому результату он приводит, чтобы внести в него необходимые изменения с целью ликвидации неравномерного ускорения и скорости движения.
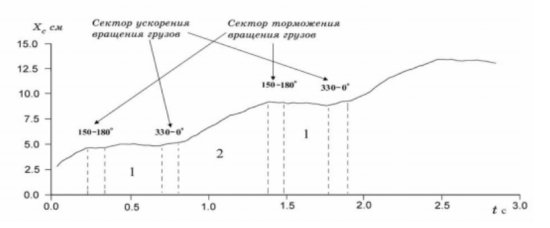
рис.6
Для этого примем, что частота вращения грузов m будет изменяться циклично с коэффициентом цикличности равным (1 + k*cos(ф)). Тогда уравнение (1) будет преобразовано в следующее
a =G*(1 + k*cos(ф))*(1 + k*cos(ф))*cos(ф) (6)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
Вычисляем скорость V через интегрирование формулы (6)
V = G*(sin(ф) + k*(ф + sin(2ф)/2) + k*k*sin(ф)*cos(ф)*cos(ф) ) (7)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
Вычисляем путь S через интегрирование формулы (7)
S = G*(-cos(ф) + k*(ф*ф/2 +cos(2ф)/4) — k*k*cos(ф)*cos(ф)*cos(ф)) (8)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
При k = 0 у нас получается осциллятор, а при k = 1 получаем, предположительно, мощный движитель, который перемещается пропорционально квадрату «накрученных» радианов. Но имеется заметный гармонический компонент. То есть, скорость и путь будут возрастать соответственно линейно т квадратично, доля гармонических компонентов по мере увеличения скорости и пути будет уменьшаться. Но это и понятно, закон инерции.
/*/
Если изменять радиус R по закону R*(1+k*cos(ф)), то получаем для ускорения такую формулу:
a =G*(1 + k*cos(ф))*cos(ф) (9)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
Через интегрирование (9) получаем скорость
V = sin(ф) + k*(ф/2 + sin(2ф)/4) (10)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
Через интегрирование (10) получаем пройденный путь S
S = - cos(ф) + k*(ф*ф/4 — cos(2ф)/8) (11)
Где G= 2*m*R*w*w/(M+2m)
m — масса m,
M — масса M,
R — расстояние массы m от оси О1,
w — угловая частота вращения
ф — угол ф
0<=k<=1
Сравнение последних формул (6), (7) и (8) с аналогичными (9), (10) и (11) показывает, что для создания тяги, якобы, лучше управлять неравномерностью частоты вращения, так как скорость и путь наращиваются быстрее примерно в два раза при каждом обороте. Но управлять изменением радиуса проще, кроме того в этом случае можно легко увеличить число грузов, что позволит сделать тягу, скорость движения более равномерным. Кроме того, неравномерность частоты вращения грузов в интервале от 0 до 360 градусов приводит к неравномерности центробежной силы и неравномерной скорости вращения грузов вдоль окружности. Такие процессы наукой пока изучены плохо, а математический аппарат не развит.
Например, можно использовать такой инерцоид (рис.7) с четырьмя грузами, в котором изменяется радиус вращения грузов (роликов) при постоянной частоте вращения маховика. Можно использовать маховик любого, с учётом прочности материалов, диаметра с любым количеством грузов (роликов) при постоянной частоте вращения. Таким образом можно компенсировать потерю мощности при отказе управлять частотой в пользу управления радиусом вращения грузов. Тем более двигателю, вращающемуся движитель, легче вращаться на одной частоте, чем менять резко за короткий период времени частоту вращения мотора с помощью разных электронных схем.
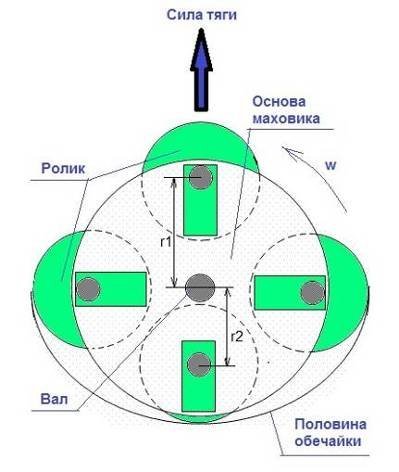
Рис.7.
/*/
Проведя поверхностный математический анализ, мы теперь знаем основные свойства инерцоида. Узнали, как изменяется его тяга в зависимости от того, каким параметром мы управляем — M, m, w, R или k — коэффициент неравномерности выбранного параметра (R или w). Поняли, при каком алгоритме можно вместо двух грузов использовать практическое любое их число, что позволит создавать мощные силовые установки из небольших составных частей.
Остаётся провести моделирование в программе «Живая физика». Одна модель будет имитировать алгоритм А.Б. Бережного, а другие модели будут имитировать изменение других параметров. В частности изменение длины прутов можно смело заменять на изменение масс грузов. Но при этом учитывать закон сохранение масс, пряча излишнюю на данный момент массу в корпусе инерцоида. В моделях постараюсь параметрам присваивать близкие значения, чтобы результаты моделирования были сопоставимы. Для меня главное наглядно убедиться, что центробежная сила способна «работать» в качестве тяги в транспортном устройстве.
/*/
Начнём проводить эксперименты в «Живой физике». Для начала посмотрим, как поведет себя инерцоид, если грузы будут вращаться в постоянной угловой скоростью. То есть, изучим простой осциллятор, который пока еще не стал инерцоидом, но по его поведению мы уже сможем составить первое впечатление, и решить, стоит ли игра свеч. Вот так выглядит результат эксперимента (рис.8)
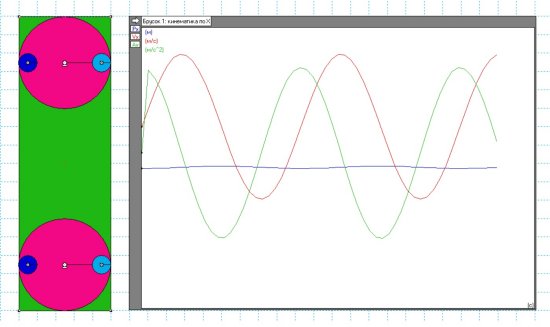
Рис.8
На рис.8. показан часть скана окна программы «Живая физика». Слева «осциллятор», справа окно индикатора, на котором отражаются ускорение, скорость и путь зеленого бруска. Зеленый, красный и синий графики — это соответственно ускорение, скорость и смещение всей платформы. Прекрасно видно, что ускорение и смещение платформы находятся практически в противофазе.
Размеры компонентов осциллятора большие.
Зеленый брусок: длина — 160 м, ширина — 54 м, масса — 200 кг.
Красные круги: у каждого диаметр — 54 м, масса — 20 кг.
Голубые кружки: у каждого масса по 100 кг.
Синие кружки; у каждого масса по 1 кг.
Оба красных кружка вращаются в противоположных направлениях с угловой скоростью в 1 рад/с. Верхний круг вращается по часовой стрелке, а нижний против часовой.
Рис.8 показывает, что центр масс зеленого бруска колеблется по гармоническому закону, амплитуда колебаний более 10 м. Перемещение зеленого бруска во время проведения эксперимента было заметно невооруженным глазом. Каждое деление на рис.8 — это 10 м. Зелёный брусок смещался от центра на 10 м влево, а затем также на 10 м смещался вправо. В сумме получалось 20 м. Естественно, вместе с зелёным бруском смещались и все части осциллятора.
Казалось бы, что такое поведение системы в ответ на вращение грузов соответствует закону сохранения центра масс: груз смещается направо — остальное всё смещается налево. Или наоборот. Но когда я посмотрел на кривые скорости и ускорения зеленого бруска, то стало ясно, что центробежные силы порождают не просто смещение общего центра масс, но делают это с большой скоростью и ускорением. То есть, благодаря центробежным силам, создаваемых голубыми грузами по 100 кг каждый весь осциллятор превращается в источник пульсирующей силы, который можно использовать для самых разных целей.
Получается, по сути, усилитель мощности. Остается перевести линейные перемещения осциллятора во вращение, посадить на ось вала электрогенератор и получать электроэнергию, мощность которой будет в несколько раз больше, чем мощность моторов, которые будут вращать дебалансы осциллятора. Эти моторы даже не будут «знать» какую мощность будут получать с осциллятора. И чем больше будет угловая скорость вращения дисков с дебалансами (грузами), тем больше мощности можно будет снять.
Но тут может возникнуть проблема, которая связана с инерцией осциллятора, особенно при большой массе зелёного бруска. Так что не зря, видимо, Толчин, сразу весь вес (массу) инерцоида «вложил» в вес (массу) грузов. Чтобы исключить влияние инерции «корпуса» инерцоида на результат эксперимента. При малой массе корпуса инерцоид развивает максимальное ускорение, скорость и путь вдоль оси Х.
Такие дебалансовые системы конструирует и изучает Велько Милкович. К сожалению, он, похоже, один, кто понимает значение центробежной силы. Даже у центробежной силы, которую порождает маятник с амплитудой колебаний в 90 градусов, превышение над весом маятника в нижней точке траектории составляет 4 к 1. То есть, раскаченный до амплитуды 90 градусов маятник увеличивает свою тягу (силу тяжести) в нижней точке в 5 раз. Конечно, эта тяга переменна, но три маятника могут сделать её практически постоянной. А потом, нам очень часто нужна именно переменная сила.
Так что осциллятор, как недоделанный инерцоид можно с высокой эффективностью использовать в самых разных конструкциях, когда нужны высокая мощность и огромные силы. И все это нам может дать всем известная центробежная сила. Которую наука на 70% не признаёт за реальную силу. Им, видите ли, она нужна исключительно тогда, когда неинерциальную систему необходимо временно «на бумаге» превратить в инерционную, чтобы она уже не нарушала СТО и ОТО. А то, как-то нехорошо получается. И при этом многие учёные не понимают, что на центробежную силу привычный нам локальный закон сохранения энергии не распространяется. Но в системе вращающееся тело-Эфир закон сохранения энергии выполняется глобально. Энергия выходит из Эфира, и в Эфир энергия возвращается. Вещественное тело является только временным аккумулятором и передатчиком энергии от одного вещественного тела к другому или от тела обратно в Эфир.
/*/
Теперь проведём по настоящему первый эксперимент. Будем использовать алгоритм Бережного. Правда пришлось немного нарушить чистоту эксперимента. Во-первых, как и в эксперименте с осциллятором использовались два груза на каждом вращающемся круге. Но теперь для верхнего круга, который вращается по часовой стрелке, масса грузов изменяется так — если груз идет вниз, то его масса равна 100 кг, если груз идет вверх, то его масса равна 1 кг. Для нижнего круга, который вращается против часовой стрелке, масса грузов изменяется по другому — если груз идет вверх, то его масса равна 100 кг, если груз идет вниз, то его масса равна 1 кг. Остальные параметры такие же, как в самом первом эксперименты. Фактически проработанный алгоритм предполагает перемещение масс из одного груза в противоположный в тот момент, когда грузы выстраиваются с вертикалью в одну линию и при этом не влияют на смещение центра масс инерцоида.
Результат меня просто ошеломил. Вот так выглядит начало эксперимента:
Рис.9
А вот так выглядят результаты эксперимента, прерванного на 30 сек.
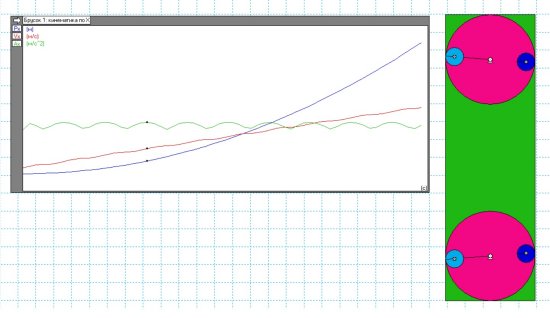
Рис.10
На индикаторе отражено поведение центра масс зелёного бруска. Зелёная линия — это ускорение, красная — скорость, а синяя — это пройденный путь. Ускорение похоже на то, что задается в алгоритме Бережного. Ускорение a пропорционально функции |cos(ф)|. Но только нижние углы кривой сглажены, скорее всего, за счёт инерции всего инерцоида. Скорость возрастает линейно с небольшой волнистостью с сдвигом по фазе по сравнению с ускорением примерно на 90 градусов. А вот пройденный путь практически возрастает по параболе, волнистость есть, но она практически не заметна. И это получено всего за 30 сек.
И дело не в конкретных полученных значениях. Главное, что пройденный путь, набранная скорость и ускорение центра масс инерцоида изменялись так, как предполагалось с самого начала. Инерцоид двигался за счет внутренних сил. Это противоречит постановлению партии и правительства, а также заверениям и теориям членов комиссии по борьбе с лженаукой. Так что комиссию надо срочно распускать. Опозорилась.
Проведём еще один опыт, в котором масса голубых грузов в правых половинах красных кругов равна 100 кг, а в левых — 10 г. Я хотел задать массу грузов, когда они оказывались левее оси вращения красных дисков значение ноль, но программа потребовала ввести любое положительное значение. Пришлось удовлетворить её требование. А также удовлетворить требованиям закона сохранения массы и удаляемую из груза массу «загонять» в массу зелёного бруска. А это целых 199 кг 980 г на два груза.
Получились следующие результаты (рис.11)
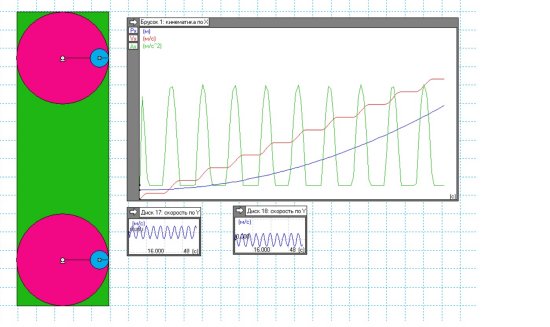
Рис.11.
Результаты в первом приближении похожи на то, что показаны на рис.10. Но теперь ускорение (зеленая линия) положительно только в половине периода, во второй половине периода оно равно нулю. Скорость (красная линия) возрастает линейно, но эдакими волнами, типа ступенек. Пройденный путь возрастает гладко по параболе, если и есть волнистость, то она практически не заметна.
Выводы. Правильно организованная центробежная сила может служить источником тяги для транспортного средства. Масса инерцоида равна примерно 250 кг, но центробежная сила обращается с ней, как с пушинкой. Такому транспортному средству, отталкивающегося от Эфира или цепляющегося за Эфир, не нужны колёса, крылья или ракетные двигатели. Нужна только энергию, которую можно получить также с использованием эфирных технологий непосредственно на самом транспортном средстве, примерно так, как это реализовал Тесла на своём электромобиле.
То есть и в этом случае получился результат поступательного движения системы за счет внутренних сил, что отвергается официальной наукой.
Теперь надо провести эксперимент с инерцоидом, у которого угловая скорость мотора, вращающего круги будет меняться в зависимости от угла поворота вращаемого круга. Сделать это можно по формуле W = Wo*(1+cos(ф)). Можно ввести перед косинусом коэффициент k, но я выбрал самый «резкий» вариант, когда k = 1. Это позволит с наибольшей наглядность оценить влияние на ускорение, скорость и пройденный путь инерцоида. Можно посмотреть, как будет вести себя инерцоид при разных частотах мотора. Но мне в данном случае достаточно оценить поведение инерцоида при одной средней угловой частоте — 1 рад/с. Остальные параметры остаются прежние.
Всё вроде бы ничего, но когда я ввел эту формулу в параметры моторов, вращающих красные диски, то получил облом. Программа не смогла рассчитать такую модель и завязла (зависла) после поворота дисков на 180 градусов, где мгновенная угловая скорость равна нулю. А нуль программа не любит. Пришлось немного изменить алгоритм и задать для угловой частоты моторов такую формулу W = Wo*(1+0.9*cos(ф)). Вроде бы ничего страшного, программа начала анализировать модель и выдавать результат. Получилась интересная картина (рис.12).
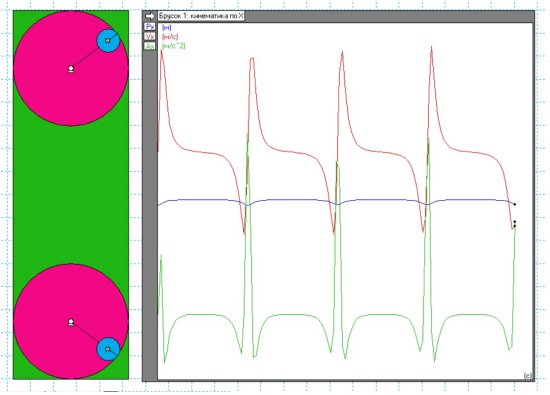
Рис.12.
Результат получился неожиданным. Кривая, отражающая ускорение (зелёная) похожа на кардиограмму. А скорость (красная) и пройденный путь (синяя) явно колеблются относительно некого среднего значения. То есть такой инерцоид ведет себя подобно осциллятору, только все кривые явно не гармоничные. Особенно меня поражает кривая ускорения. Ладно, с положительным пиком можно как-то согласиться, но вот два отрицательных зубца откуда появились? Либо что-то с программой, либо программа свела к одному центробежные силы и линейную инерцию вдоль оси Х ускорения всего инерцоида в целом, которые возникают вторично в ответ на резкие смещения инерцоида при воздействия на него центробежной силы, возникающей в «передней» части траектории грузов.
Чтобы отследить поведение модели в течение более длительного периода длительность наблюдения была доведена до 1000 с. Результат показан на рис.13. В данном эксперименте угловая частота изменялась как в предыдущем опыте, но использовались на красных кругах по два груза, один (голубой) тяжёлый, другой (синий) в 100 раз более лёгкий.
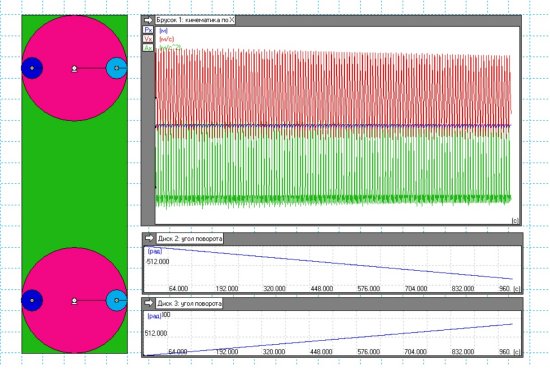
Рис.13.
За 1000 секунд центр масс инерцоида практически не сдвинулся с места. Имеет место волнообразная кривая, центр смещается чуть вправо, затем чуть влево, оставаясь в среднем на одном месте. Если кто-то посчитает, что в этом виноваты синие грузы, то хочу заметить, что масса их равна 1 кг, тогда как масса голубых грузов 100 кг. На нижних двух индикаторах показано как меняется углы, которые «накручивают» моторы (верхний и нижний). Это сделано для того, чтобы было видно, что моторы вращаются, а центр инерцоида практически стоит на месте. Моторы вращаются, диски с грузами вращаются, частота вращения моторов изменяется по немного другому закону W=Wo*(1+cos(ф)/2). Но результат тот же, что и на рис.12. Получается, что плавное изменение частоты вращения грузов не приводит к перемещению инерцоида.
Был проведён ещё один эксперимент (рис.14). В данном случае когда грузы находились в правой половине красных кругов, то угловая скорость моторов была равна 1 рад/с. А когда грузы находились в левой части красных кругов, то угловая скорость моторов равнялась 0.5 рад/с. Получилось то, что получилось
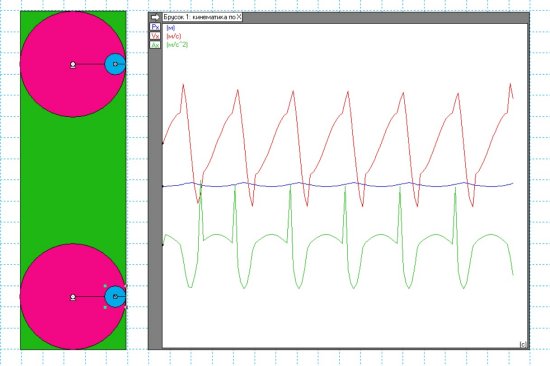
Рис.14.
Опять облом. Результат в очередной раз подтвердил, что изменяя частоту вращения грузов, вращая их спереди быстрее, чем сзади, никакого перемещения центра масс инерцоида получить не удается. Видимо это связано с тем, что среднее ускорение, которое получает инерцоид одинаково как спереди, так и сзади. Если центробежная сила сзади уменьшается, то при этом одновременно увеличивается время действия уменьшенной центробежной силы. Поэтому получается осциллятор, колебания которого далеки от гармонических. Но не исключаю, что программа «Живая физика» не способна учитывать все тонкости, связанные с вращением тел.
Была сделана попытка проверить, как отразится на поведении инерцоида другой вариант изменения скорости вращения красных кругов. Когда грузы (голубые кружки) двигались справа налево, то угловая скорость моторов была равна 1 рад/с, когда же грузы (голубые кружки) двигались слева направо, то угловая скорость моторов была равна 0,5 рад/с. Результат на рис.15.
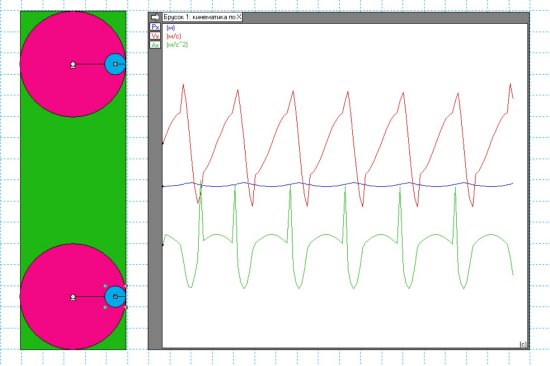
Рис.15.
Опять получается осциллятор. Хотя вид кривых, показывающих изменение положения, скорости и ускорения центра масс инерцоида по сравнению с предыдущим опытом изменился. Очередной облом, или показатель того, что программа «Живая физика» не умеет правильно работать с вращающимися телами. Скорее всего именно так, так как в документации на эту программу я не видел глав, объясняющих как правильно моделировать такие объекты, как гироскопы, маховики и волчки. А ведь в нашем случае грузы представляют из себя хоть и уродливые, но маховики, которые в инерцоиде Толчина двигаются по окружности с неравномерной угловой скоростью. Но этот момент мы обсудим специально.
Выходит, если руководствоваться результатами моделирования в программе «Живая физика», что управлять тягой инерцоида, изменяя плавно или с разрывом частоту вращения грузов в интервале от 0 до 360 градусов от некого максимального значения к минимальному, не получается. Но частотой как параметром управлять можно, но только как постоянным параметром, меняя его только при необходимости изменения тяги в несколько раз. Ускорение инерцоида квадратично зависит от частоты вращения грузов. Увеличили частоту вращения грузов в 4 раза, получили увеличение тяги в 16 раз, уменьшили частоту в два раза, то получаем уменьшение тяги в 4 раза. И т. д.
Получается, что управлять тягой инерцоида (центробежным движителем) можно, но надо всё правильно закладывать на уровне проектирования движителя. Вариантов тут можно предложить если не много, то несколько. Кое что удалось узнать в процессе проведения экспериментов в программе «Живая физика».
Проверять на поведение инерцоида изменение тяги путём изменения длины прутов, на концах которых висят грузы я не стал, так как укорочение прута можно заменить пропорциональным уменьшением массы грузов. Что и было сделано в эксперименте по моему алгоритму, где масса грузов на определенных участках траектории приравнивалась нулю с переносом «излишка» масс в корпус инерцоида. А изменение массы до нуля можно заменить приравниванием нулю длины прутов при сохранении массы грузов. Зависимость получается той же самый.
Меня волнует другое. Почему у Толчина инерцоиды перемещались и создавали тягу, если он только изменял частоту вращения грузов? Ведь эксперименты показали, что возникающие центробежные силы, приведенные не к углу поворота грузов, а к временной равномерной шкале, не создают тяги вдоль оси Х. Надо подумать и хорошо изучить основную работу Толчина «Инерцоид. Силы инерции как источник поступательного движения». Возможно секрет инерцоида Толчина заключается во взаимодействии двух видов инерции — поступательной (продольной) и центробежной (радиальной). А также конструктивными особенностями инерцоида Толчина, что позволяло «скрытно» менять такой параметр как радиус вращения грузов. То есть, в период «разгона» грузов длина прутов, на концах которых крепился груз, увеличивалась, а в момент «торможения» длинна прутов уменьшалась. Тогда такой инерцоид мог создавать итоговую «положительную» тягу в горизонтальном направлении. Или если в таком же порядке менялась некая функциональная масса, что также приводило бы к увеличению центробежной тяги в горизонтальном направлении. Как бы не дикой казалась такая версия, но проверить её следует, так как длина прутов или массы грузов могла изменяться не только физически, но и функционально.
Есть еще одна версия которая может быть проверена экспериментально. Дело в том, что грузы являются маховиками, хоть и странной формы. А если так, то для них должны быть справедливы законы, которые заставляют маховики прецессировать и нутировать. Когда груз в инерцоиде Толчина проходит область ускорения, то на груз давит сила инерции, которая направлена против направления движения груза. Если же груз тормозится, то на него давит сила инерции, которая направлена по направлению движения груза. Так как ускорение и торможение дисков осуществляется в диаметрально противоположных областях, то силы инерции направлены в одну сторону и для грузов являются своеобразной силой тяжести, действующей в разные моменты времени на маховик из груза. Под действием такой силы маховик должен прецессировать, то есть подвергаться действию силы прецессии. А так как эта сила направлена перпендикулярно действию создаваемых импульсов силы при ускорении и торможении, то инерцоид по идее должен перемещаться рывками по направлению силы, которая формирует прецессию маховиков из грузов. И если силы инерции действуют в инерцоиде Толчина по вертикали, то сила прецессии должна действовать горизонтально, вызывая ускорение вдоль оси Х. Программа «Живая физика» на такой анализ, похоже, не способна, поэтому нужен живой эксперимент.
По моим предположениям, в соответствии с теорией Эфира русского дилетанта без формул в точках 0 и 180 градусов будут создаваться соответственно области с пониженным и повышенным давлением Эфира. В этих областях давление Эфира будет пульсировать. Причем вначале в зоне 0 градусов будет создаваться воронка с пониженным давлением Эфира, куда инерцоид будет затягиваться как в болото, затем по мере смещения грузов эта воронка исчезнет и инерцоид перейдёт в движение по инерции. Когда грузы войдут в область 180 градусов, там появится холм с повышенным эфирным давлением, который будет толкать инерцоид вперёд, а груз по окружности. После выхода грузов из области 180 градусов холм с повышенным эфирным давлением рассосётся и инерцоид опять будет двигаться по инерции до области 0 градусов.
Такой эксперимент может провести тот, в чьём распоряжении уже есть готовый инерцоид, у которого вращением грузов можно управлять с помощью компьютерной программы. Надеюсь, что в команде Г.И.Шипова найдётся такой инерцоид. И ему ничего не стоит проверить это предположение. Может уже и проверяли. Формирование динамических эфирных воронок и холмов должно сопровождаться электромагнитными явлениями, обнаружить которые можно с помощью датчика Холла или его аналогов, прикреплённых к грузу.
/*/
Что мы получили в результате теоретического и практического моделирования инерцоида.
Во-первых, доказано, при условии, что программа «Живая физика» правильно работает с центробежными силами, что центробежная сила при адекватных организации и управлении способна стать источником безопорной (эфироопорной) силы. Или силы, создаваемой за счёт внутренних источников системы, перемещающей саму себя. Не в нарушение законов Ньютона, а в полном согласии с ними. Так что некое постановление, запрещающее патентовать инерцоиды, надо отменять. Это самое главное, что получено в серии проведённых экспериментов в программе «Живая физика». Теперь любой учитель физики, а с ним любой ученик с помощью подобного программного средства сможет получить аналогичный результат.
Во-вторых, обнаружены феномены, которые никак не ожидались перед моделированием. Эти вновь открытые феномены требуют своего изучения, но опять же в рамках существующих законов механики, с обязательным признанием Эфира, как источника сил и энергии. Суть феномена заключается в невозможности в рамках программы «Живая физика» создания тяги исключительно за счёт «периодического» в течении одного оборота грузов изменения угловой скорости вращения грузов. Произведения мгновенно создаваемой центробежной силы (тяги) на период её создания и существования оказывается величиной постоянной. Поэтому интегрирование векторов создаваемых центробежных сил сил по времени за один оборот в 360 градусов дает ноль. В результате инерцоид превращается в осциллятор, способный только колебаться сложным образом относительно общего центра масс. Но если предположить, что программа «Живая физика» не способна правильно отображать гироскопические эффекты, то есть надежда, что эти странные феномены перестанут проявляться в более совершенном компьютерном симуляторе механических процессов, если, вообще, такая программа существует. Или провести реальный физический эксперимент с уже действующим инерцоидом, у которого придется слегка подкорректировать управление движением грузов и установить датчики Холла для регистрации эфирного потенциала как индикатора создания эфирных барических ям и холмов, возникающих при разгоне или торможении грузов в точках 0 и 180 градусов.
/*/
Мне после прочтения работы В.А.Жигалова «Ещё раз о движении инерциоида Шипова» так и не удалось в приведённых графиках увидеть пройденный инерцоидом путь. Вот рисунок из статьи (рис.16)
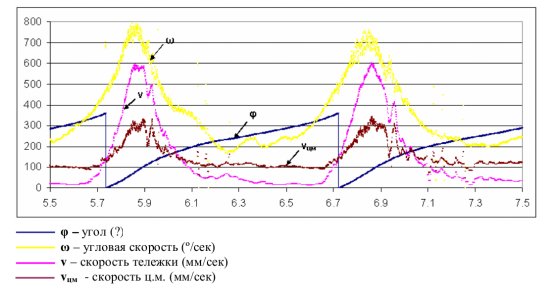
Рис.16.
На рисунке есть угловая скорость грузов, скорость груза и центра масс инерцоида, угол поворота грузов. Но нет пройденного пути, по которому можно с уверенностью судить, двигался ли при этом инерцоид или колебался на месте. Судя по положительным значениям скоростей можно предположить, что инерцоид двигался, но для полной уверенности на графике пройденный путь должен присутствовать. Ось Y данного графика точно отражает динамику ф от 0 до 360 градусов. Видно, что ф измеряется в градусах. А вот относительно какого нулевого значения пляшут угловая скорость w, скорость перемещения груза по горизонтали V и скорость движения центра масс инерцоида Vцм, ясности нет. Если инерцоид перемещался с переменным, но постоянным средним ускорением, то графики скорости должны возрастать линейно. А на графике возрастания нет, есть только колебания относительно неких средних значений, а это заставляет меня предположить, что и пройденный путь колебался вокруг некого среднего значения, но на графике эта кривая не отражена.
У меня нет никаких темных желаний негативно оценивать работы Г.И.Шипова. Тем более фактов, что его инерцоиды показали прекрасные «ходовые» качества во многих экспериментах как в России, так и за рубежом, множество. Я просто выступаю за то, чтобы на подобных графиках обязательно отражались данные по пройденному пути, скорости и ускорении центра тяжести инерцоида. Тогда, глядя на такой график, всегда можно чётко определить, все главные кинематические характеристики исследуемого объекта.
Мне кажется, что график зависимости угловой скорости грузов должен быть примерно таким (рис.17)
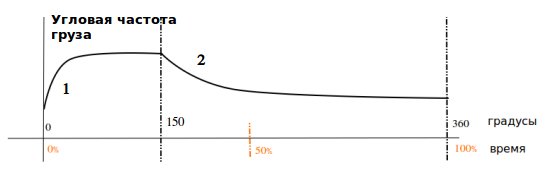
Рис.17.
В первые 30 градусов (область 1) угловая скорость грузов под воздействием пружины или мотора резко возрастает по логарифмической зависимости, достигнутая скорость по инерции держится на одном уровне до 150 градусов (область 2), затем до 180 градусов осуществляется торможение тормозным устройством (по логарифмической кривой). После чего грузы опять движется по инерции до 360 градусов текущего цикла, или до 0 градусов нового цикла, сохраняя постоянной угловую скорость. На данном графике трение не учитывается. Но даже учёт трения при хорошей смазке не сильно бы изменил график. Ну, может быть немного сделал бы наклонными горизонтальные участки графика. Такой зависимости я на рис.16 не вижу.
Ещё один момент, мы должны помнить, как нас дергает в автобусе, если водитель неопытный, резко газует или тормозит. Так и в инерцоиде Толчина вначале в первые 30 градусов осуществляется резкий, но кратковременный разгон грузов, сопровождаемый резким ускорением (перегрузками). Затем до 150 градуса грузы двигаются без ускорения, с постоянной угловой и линейной скоростью. После 150 градусов происходит кратковременное, но резкое торможение, с сильными перегрузками. после 180 до 360 градусов инерцоид и грузы двигаются по инерции. Как разгон, так и торможение грузов с резкими перегрузами сопровождаются огромными силами, которые многие экспериментаторы не учитывают. Огромные импульсные силы, формируемые на участках разгона и торможения, создают большие импульсные силы прецессии, которые действуя вдоль направления движения, заставляют инерцоид Толчина перемещаться рывками. Эфирная технололгия. Короче, надо в нужном месте и нужном времени создавать резкие ускорения грузов. И чем резче будет грузы ускоряться или тормозится, тем сильнее получится сила, импульсно толкающая инерцоид в горизонтальном направлении. Ничего личного, только чистая физика. Это, похоже и есть главная тайна инерцоида Толчина. Так что есть смысл провести еще один экмперимент в программе "Живая физика", но только теперь моторов уже быть не должно, а будут две силы, которые в нужном месте и в нужное время будут короткими импульсами воздействовать на грузы, а остальное будет довершать инерция.
/*/
Почему я предполагаю, что в настоящем инерцоиде Толчина тягу создают инерция и гироскопические эффекты? Дело в том, я вспомнил о вот таком заинтересовавшем меня ранее устройстве:

Рис.18. Три колеса в колесе в сборе и в работе.
Чем такие дебалансы отличаются от дебалансов в инерцоиде Толчина? Да ничем. Только у Толчина два дебаланса, вращающиеся в разные стороны и сами себе создают дополнительное локальное эфирное поле в нужных точках и нужном времени. А на рис.18 представлено устройство, где три дебаланса вращаются в одном направлении в центробежном поле главного центрального маховика. Три дебаланса, по идее, под воздействием силы прецессии сами могут вращаться и вращать главный маховик. Но лучше три внутренних дебаланса регулярно «подкручивать», что и делает автор изобретения как в ручном режиме, так и с помощью простой системы управления. Таковы мои предположения в отношении трех колес с эксцентриками в колесе.
Как работать с этим устройством, показывалось в видео по данным адресам (см. ниже). Теперь эти видео недоступны. Это указывает на то, что этой технологией заинтересовались большие или богатые люди. А Россия по-прежнему хочет обогреваться и питаться электроэнергией с помощью газа. Или Путин В.В. пошутил, как иллюзионист, для отвода глаз?
http://www.youtube.com/watch?v=I4QwWnqQE5w
http://www.youtube.com/watch?v=wdodjuVC45k
http://www.youtube.com/watch?v=U8v7ZQiGSgE
Как жалко, что в очередной раз у землян украли прекрасную эфирную технологию. Этот аппарат требует для подкрутки трех дебалансов сущие ватты, а с главного вала можно снимать с помощью зубчатой передачи уже киловатты. Скорее всего теперь в Интернете уже не найти чертежи данного устройства. Если мы откажемся от технологии Толчина, то это будет началом большого конца человечества.
/*/
Заканчивая свой поверхностный анализ инерцоида Толчина, вынужден подтвердить вслед за Толчиным, что в его устройстве центробежные силы в качестве тяги, если и используются, то не напрямую, а опосредовано, через механизм прецессии. Инерцоид Толчина нуждается в дополнительных исследованиях с целью подтвердить или опровергнуть роль в создании тяги гироскопических эффектов. Виртуальные эксперименты в программе «Живая физика» показали огромную роль центробежных сил в создании безопорной (эфироопорной) силы, с одной стороны, и неспособность «Живой физики» моделировать гироскопические эффекты, с другой стороны. Нужна более совершенная программа.
26.02.2019
Безтопливная энергетика
На главную