Возникла идея провести анализ работы двигателей с разными вариантами возбуждения. Дело в том, что как мне кажется, механизм работы некоторых электродвигателей наукой объясняется неправильно. Поэтому хочу донести до читателя, как я понимаю этот механизм.
Известно, что окружающая нас среда в основной массе находится в покое или медленном движении, что имеющиеся приборы это движение не регистрируют. А, как известно, под лежачий камень вода не течёт.
Но если окружающую среду «замутить», заставить с помощью «статора» некий объем этой среды колебаться по заранее заданному закону, то в такой среде специально подготовленные тела («ротор») можно заставить перемещаться по заранее заданной траектории. Благодаря тому, что в «замутнённой» «статором» среде возникают зоны с чередованием повышенного и пониженного давления, которые и вращают «ротор».
В общем случае дело сводится к созданию «статором» стоячей или бегущей волны. Или чередования соллитонов (типа волны цунами), гребни которых перемещают «ротор» по заданной траектории, обычно по окружности, как наиболее простой криволинейной и замкнутой траектории.
При этом происходят странные вещи.
Во-первых, энергия для создания стоячей волны статора тратится только на разные виды сопротивлений. В электромоторах – это сопротивление обмотки статора. Если использовать сверхпроводящие статорные обмотки, то можно создать моторы, которые практически не будут тратить энергии на возбуждение этих обмоток.
Во-вторых, на статоре положительные волны колебаний суммируются с отрицательными волнами, что в итоге дает энергетический ноль. Поэтому, как только мотор останавливается, среда около статора моментально приходит в исходное незамутнённое состояние.
В-третьих, элементы ротора перемещаются по заданной траектории уже совершенно «бесплатно», опираясь на возникшие в стоячей или бегущей волне градиенты давления. Частота и мощность вращения ротора определяется мощностью колебательного процесса на статоре.
В-четвертых, в электромоторе реализуется типичный параметрический резонанс. Но это только в том случае, если частота колебаний на элементах статора жестко связана с частотой вращения ротора. Поэтому конструкция электромотора должна иметь возможность определять частоту колебаний на элементах статора частотой вращения ротора, а не оборот. Промышленная частота вращения роторов многих моторов 3000 об/мин. Это 50 гц. Это частота переменного тока. Но такая частота годится для мотора, в котором имеется по одному элементу на роторе и статоре. Если на роторе и статоре имеется по три или четыре элемента, то частота колебания на статоре такого мотора должна быть, соответственно, 150 или 200 гц. А так как основная часть электромоторов работает на частоте 50 гц, то именно с этим связан такой факт, как низкий КПД многих электромоторов, который объясняют наличием ПЭДС. И, скорее всего, это так, только многие не понимают, что ПЭДС появляется именно из-за расхождения частоты возбуждения статорных элементов и частоты вращения ротора.
В-пятых. Раз частота задающего генератора на статоре должны быть согласована с частотой вращения ротора, то мотор должен быть всегда подключен к дополнительной нагрузке. Чтобы при слабой основной нагрузке стабильную частоту вращения можно было поддерживать подключением дополнительной нагрузки, сумма которых должна соответствовать паспортным данным электромотора. Генератор на Саяно-Шушенской ГЭС, возможно, разрушился и вылетел в зал потому, что он лишился на короткое время положенной для его работы нагрузки. Он, скорее всего, работал в режиме параметрического резонанса. А с параметрическим резонансом шутить нельзя.
Поэтому была поставлена серия экспериментов в «Живой физике», чтобы проанализировать перечисленные эффекты.
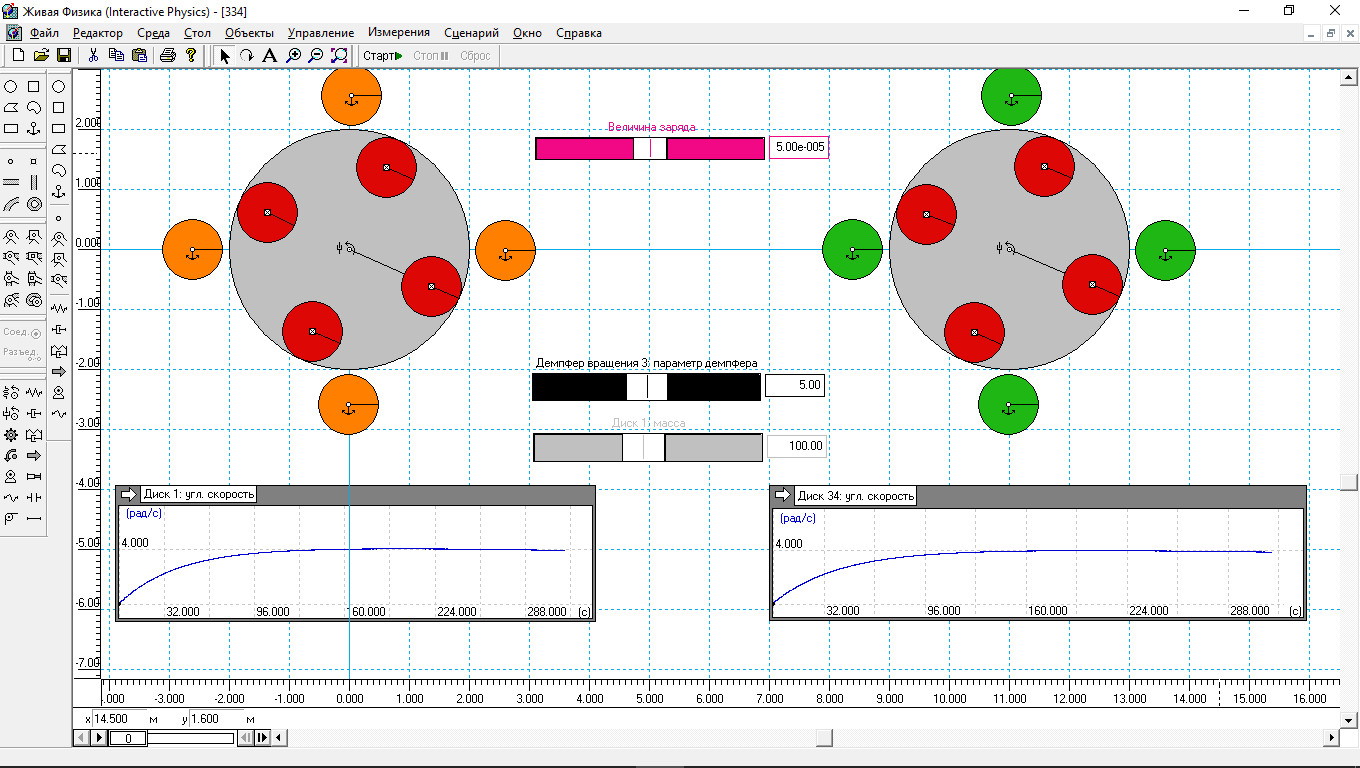
Итак, опыт №1 (рис.1)

Рис.1.
На рис.1 показан скан окна программы «Живая физика» после остановки эксперимента, в котором исследовались два одинаковых мотора. На левом моторе статорные элементы оранжевого цвета, все закреплены якорями. На правом моторе статорные элементы тоже закреплены якорями равномерно вокруг ротора. Цвет элементов зелёный.
Ротор в обоих моторах одинаковый. Это диск, посаженный на демпфер вращения, на котором равномерно размещены 4 элемента – 4 красных диска. При работе мотора серый диск вместе с красными дисками вращается вокруг демпфера вращения.
Все красные диски заряжены положительно, величина заряда указана на розовом регуляторе наверху посередине между моторами. Величина заряда равна 5e-5к.
Оранжевые и зелёные статорные диски в процессе работы мотора синхронно (одновременно) меняют свою полярность по гармоническому закону. По синусу. Максимальная величина заряда этих дисков тоже определяется розовым регулятором.
В модели есть еще 2 регулятора. Чёрный регулятор задаёт параметр демпфера вращения. В данном эксперименте его величина равна 5. При уменьшении этого параметра максимальная частота вращения ротора увеличивается, при увеличении – уменьшается. А самый нижний регулятор показывает массу серых дисков, которые играют роль маховиков моторов. Этот показатель установлен на 100 кг.
Под каждым мотором располагается индикатор, которые регистрируют угловую скорость вращения роторов. По результатам эксперимента можно сделать вывод, что у одинаковых моторов угловая скорость роторов изменяется одинаково.
В поле заряд у оранжевых дисков введена формула:
input[58]*sin(4*body[1].p.r) (1)
для зеленых формула немного иная, так как теперь опорным является серый диск правого мотора, а у него номер [34].
input[58]*sin(4*body[34].p.r) (1а)
где input[58] – это данные розового регулятора [58], а body[1].p.r – это угловая скорость вращения ротора (серого диска) левого мотора. body[34].p.r – это угловая скорость вращения ротора (серого диска) правого мотора. 4 – число статорных и роторных элементов.
Теперь поставим опыт №2, где во втором моторе заставим заряд на статоре изменяться по закону:
input[58]*sin(2*body[34].p.r) (2)
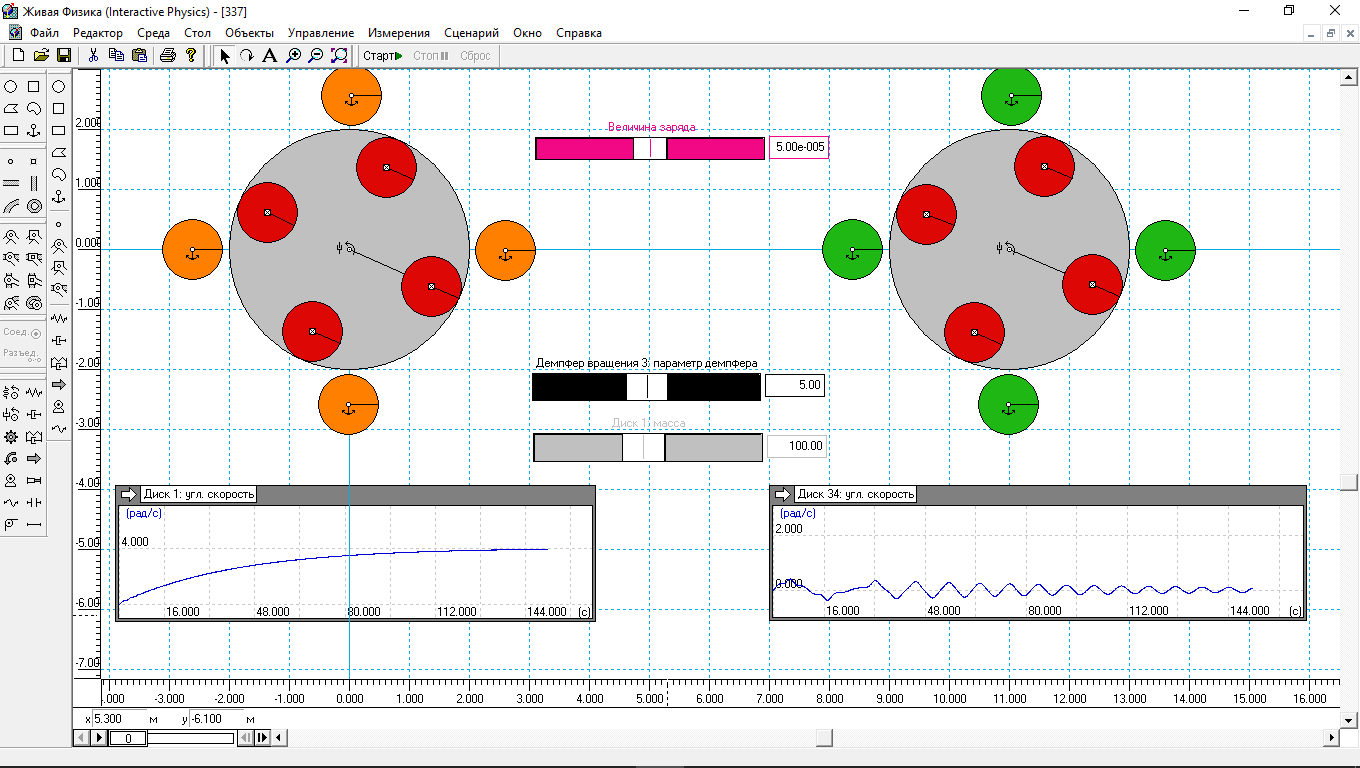
Рис.2. Частота возбуждения статора уменьшена в 2 раза.
Кроме изменения частоты возбуждения статора, других изменений в модель не вносилось.
Результат говорит сам за себя. Уменьшение частоты возбуждения статора в 2 раза парализовало работу двигателя, ротор перестал вращаться. Этот опыт показывает, что для нормальной работы мотора крайне важно подобрать частоту параметрического возбуждения статорных обмоток. Крайне важно, чтобы каждый роторный элемент «перемещался» на гребне свой и только своей волны.
Это было проверено в следующем эксперименте (рис.3)
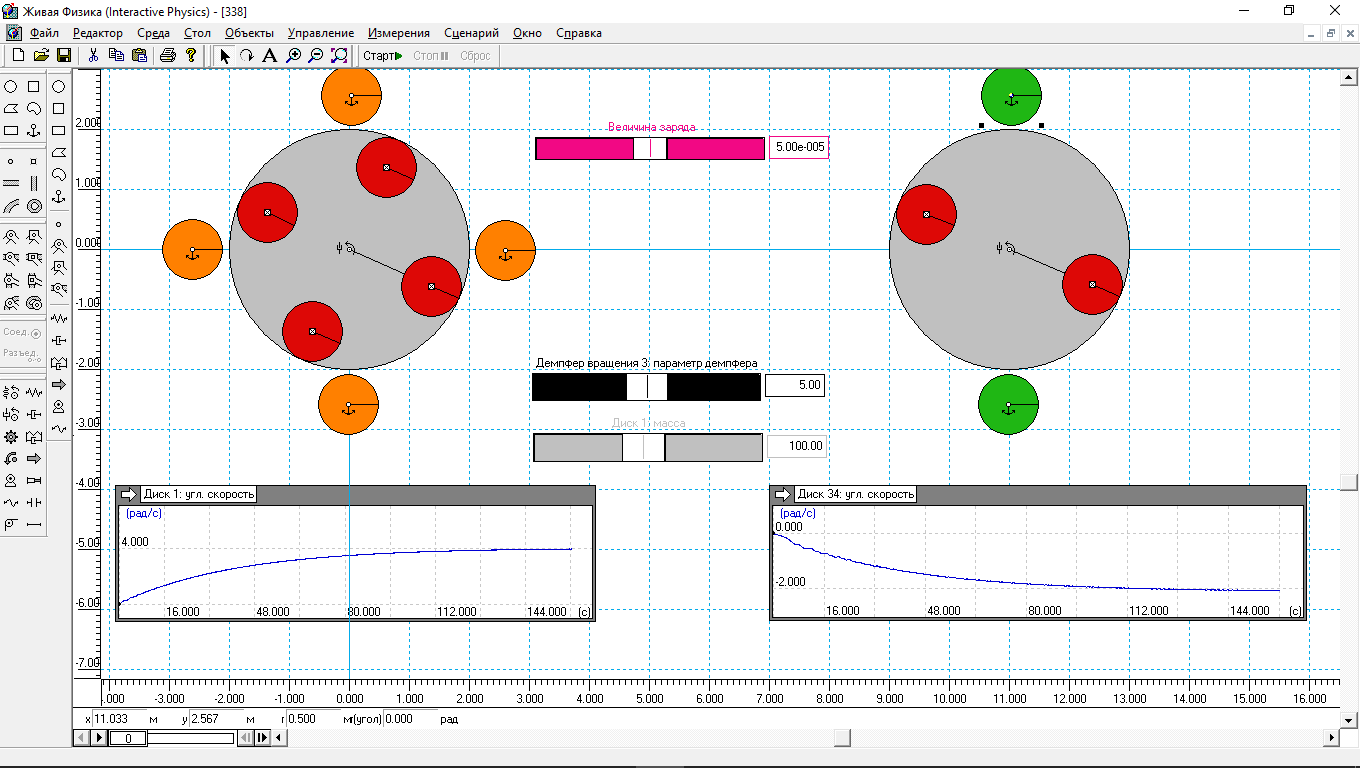
Рис.3.
На этом рисунке у правого мотора оставлены по два статорных и роторных элемента. Заряд статорных зелёных элементов изменяется по формуле (2).
Видно, что ротор стал вращаться по часовой стрелке. И угловая скорость его достигла только 2 рад/с. У мотора слева этот показатель в два раза больше.
Теперь попытаемся сделать так, чтобы у правого мотора на роторе были установлены два элемента разной полярности, а также статорные элементы работали в противофазе. Этим самым мы надеемся получить улучшенные результаты, чем в варианте 3. Проверим. (рис.4).
Теперь в правом двигателе левый статорный элемент работает по формуле:
-input[58]*sin(body[34].p.r) (3),
А правый по формуле :
input[58]*sin(body[34].p.r) (4)
То есть, статорные элементы правого мотора работают в противофазе, а два элемента на роторе имеют разные заряды.
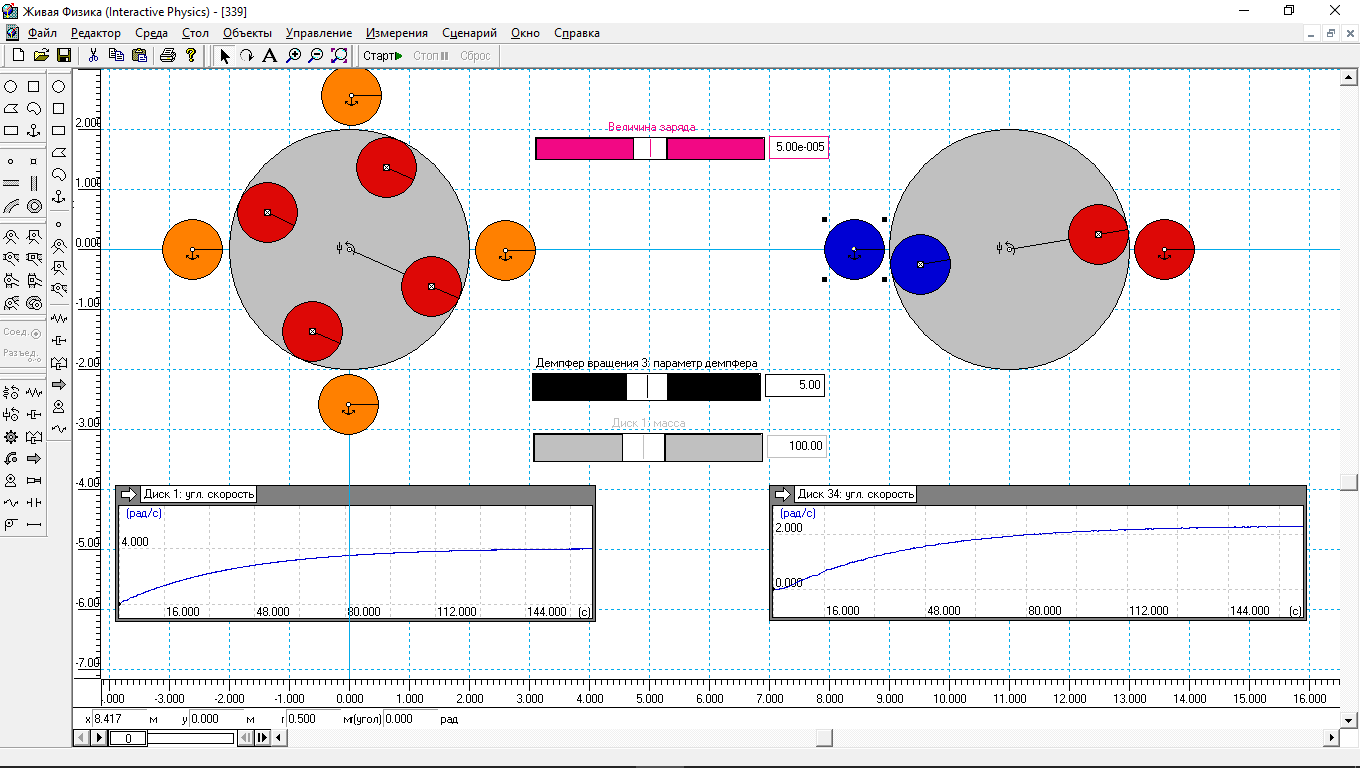
Рис.4.
Результат работы правого мотора практически такой же, как и в предыдущем эксперименте. Так что нет смысла мудрить с намотками как роторных, так и статорных обмоток, если используются они. Или мудрить с «правильной» установкой полярности магнитов ротора. Стандарт – есть стандарт. И никаких проблем.
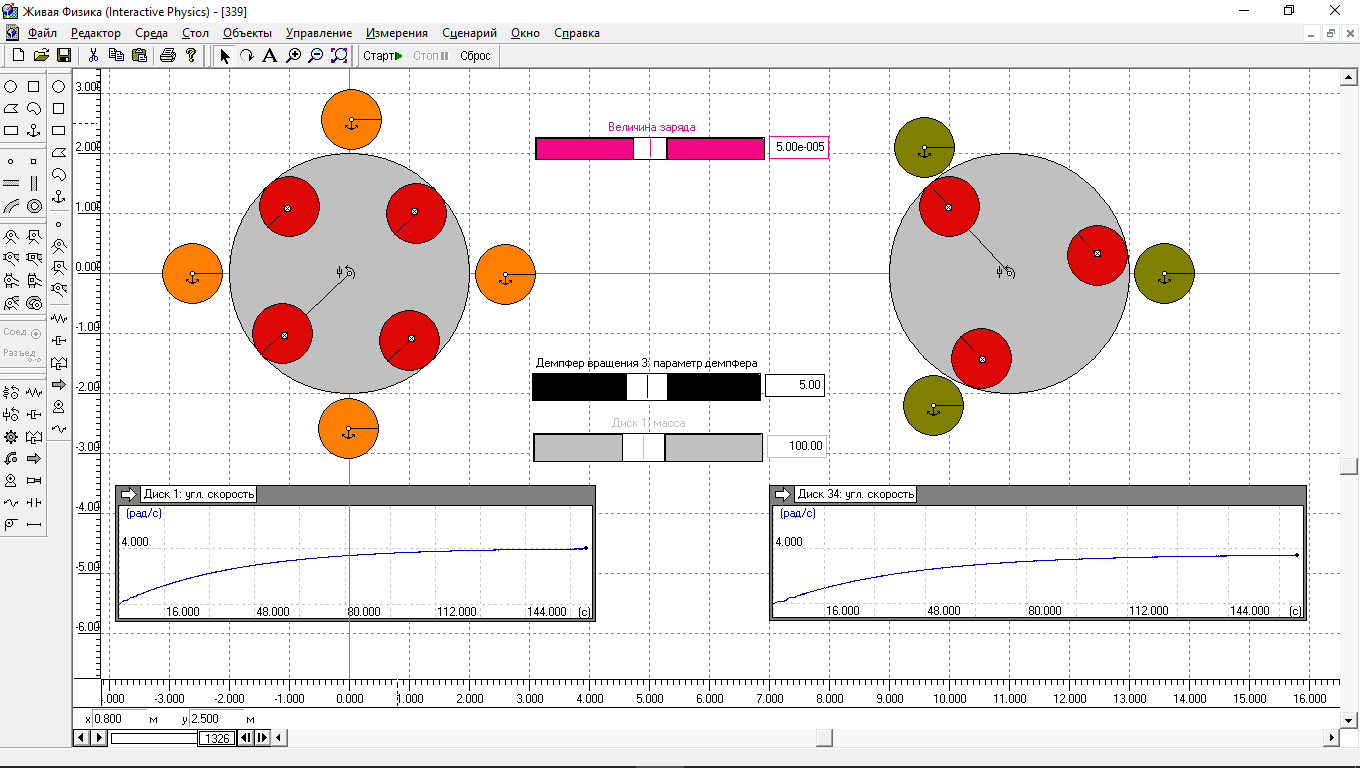
Рис.5.
На рис.5. представлены результаты эксперимента с мотором, у которого имеется по три статорных и роторных элемента. У статорных элементов правого мотора полярность меняется по формуле:
input[58]*sin(3*body[34].p.r) (5)
ибо теперь у нас на статоре три элемента.
Результат моделирования показывает, что угловая скорость ротора правого мотора примерно равна 3.5 рад/с. В пересчете на один роторный (статорный) элемент этот результат даже выше, чем у левого мотора. Но различие незначительное, чтобы его принимать во внимание. А если этот результат моделирования в будущем использовать, то только исходя из других параметров. Таких, как расход металла на один элемент, или какой вариант проще для изготовления в промышленных условиях и т.п. В крайнем случае, подгонять мотор с тем или иным количеством элементов на роторе и статоре под заданную мощность или угловую скорость можно и через изменение их заряда (силы магнитов или электромагнитов).
Все выше рассмотренные модели возбуждались с помощью гармонических сигналов на статорных элементах. Теперь сравним, как изменятся показатели мотора, если вместо гармонического сигнала мы используем прямоугольные импульсы. Начнем с самого простого случая, с преобразования синусоиды в прямоугольный импульс – меандр (рис.6).
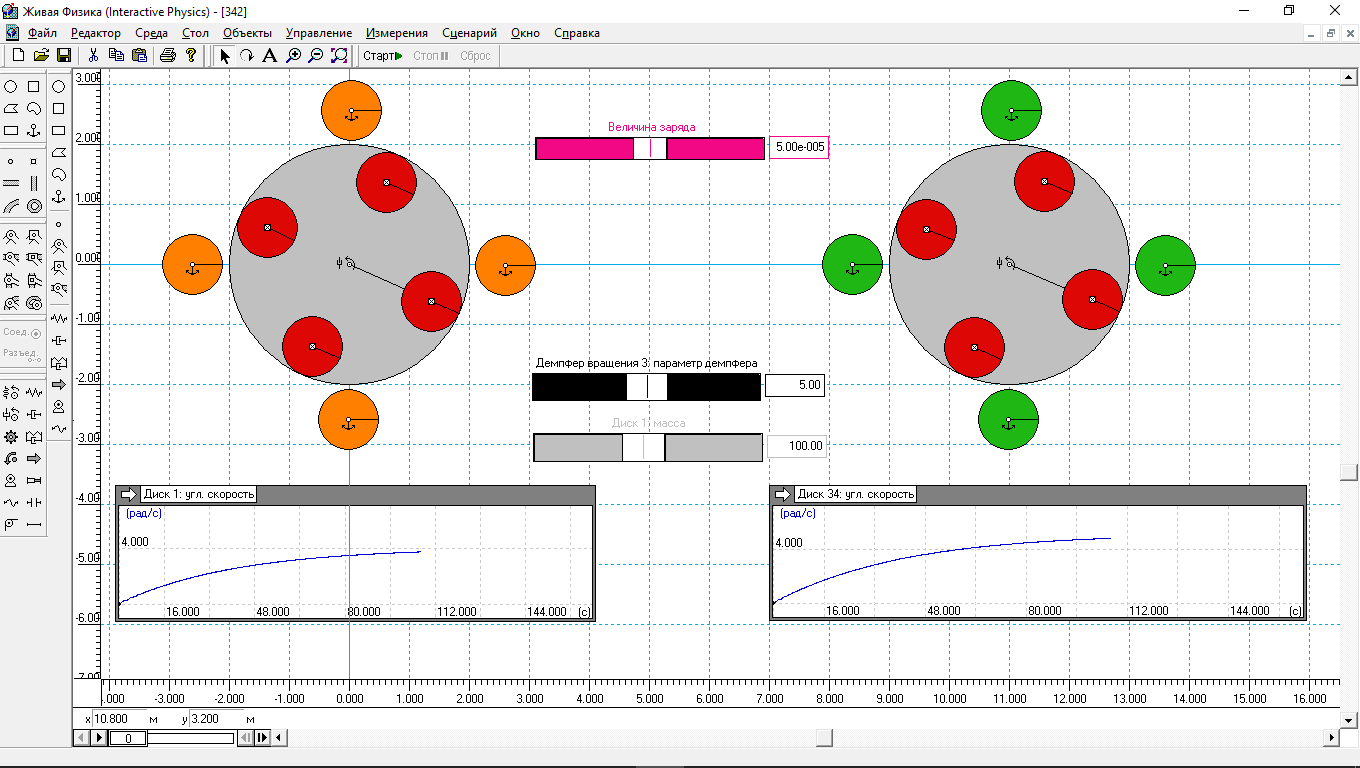
Рис.6.
Если в левом моторе заряд статорных элементов изменялся по формуле (1), то в правом по формуле:
input[58]*sign(sin(4*(body[34].p.r))) (6)
Результат моделирования показывает, что изменение зарядов статора по закону «прямоугольного» синуса приводит к повышению угловой скорости на 20%. Вместо 4 рад/с угловая скорость ротора правого мотора установилась на уровне 5 рад/с. Эффект положительный, конечно, есть. Но синусоиду создавать проще, так что и тут можно дать рекомендации принимать решения о выборе того или иного метода возбуждения статорных элементов «на месте», исходя из дороговизны или дешевизны тех или иных решений.
Теперь осталось, как это принято считать в академических кругах, оценить влияние на угловую скорость ротора таких показателей прямоугольных импульсов, как фаза, скважность и амплитуда импульсов.
Сразу следует отметить, что исследовать влияние на поведение модели такого фактора, как фаза, нет смысла, так как в процессе вращения элементы ротора в итоге примут наиболее выгодное в энергетическом отношении «положение» между гребнями волн, создаваемых элементами статора.
В природе очень редко наблюдаются резкие переходы и перепады, за исключением случаев, которые имеют место, например, в ударных волнах, или таких природных феноменах, как глубокие ущелья или отвесные горные склоны. Но даже в этих случаях их можно представить в виде гармонической функции с коротким периодом и большой амплитудой, которые в моделях позволяют достаточно точно отразить основные функции.
В большинстве случаев многие периодические процессы достаточно точно описываются гармонической функцией или суперпозицией нескольких (не более 5) гармонических функций. А часто, как показывает анализ на простой модели, можно с высокой точностью использовать простой меандр. Особенно когда точность особо не нужна, а важно сравнить два или несколько похожих варианта. И в этом случае модель, созданная в программе «Живая физика», позволяет получить первые и достаточно точные результаты.
При этом, правда, следует всегда помнить, что для численных расчетов использовать функции, типа меандра или дельта-функция Дирака, нежелательно. Так как всегда есть вероятность, что можно получить «неожиданный» результат, так как трудно обеспечить стабильность расчетов.
В качестве примера для анализа влияния увеличения амплитуды колебания зарядов на статорных элементах можно привести результат моделирования поведения моторов на разный вариант возбуждения – синусом и меандром. При этом амплитуда «сигнала» увеличена всего в полтора раза как для правого, так и для левого мотора. Причина в том, что при большем коэффициенте либо начинается проявляться неустойчивость вычислений, либо результат моделирования показывает, что при угловой скорости в 4 и более рад/с «заклёпки» не выдерживают, и мотор начинает разрушаться.
Результат моделирования представлен на рис.7.
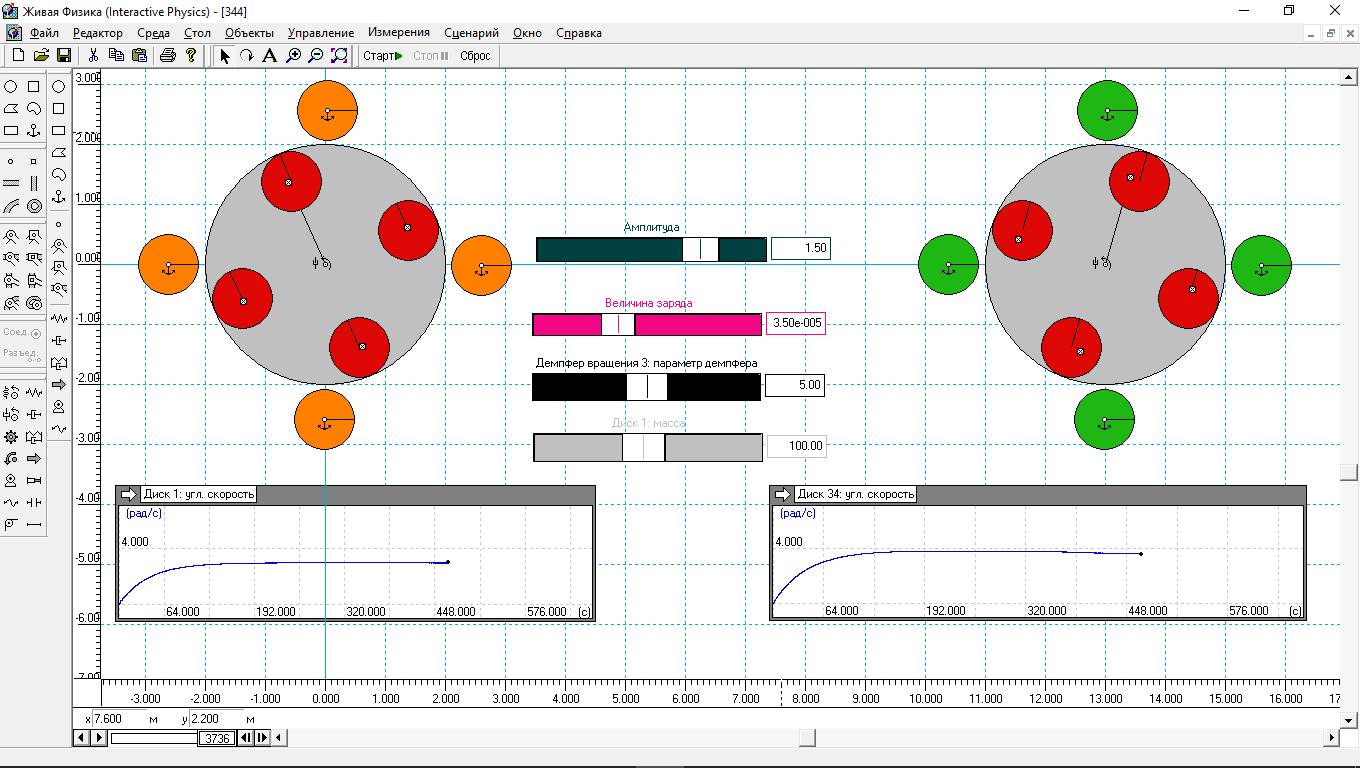
Рис.7.
По сравнению с другими моделями в схему добавлен регулятор, позволяющий устанавливать значение множителя для амплитуды колебания зарядов на статорных элементах. В данном случае этот коэффициент равен 1.5.
Формула для заряда левого диска теперь выглядит так:
input[63]*input[58]*sin(4*body[1].p.r) (7)
а для правого мотора так:
input[63]*input[58]*sign(sin(4*(body[34].p.r))) (8),
где input[63] – это данные с регулятора для настройки амплитуды колебаний зарядов на статоре.
Анализ рис.7. показывает, что на правом моторе при угловой скорости около 4 рад/с начались деформации, роторные диски смещаются относительно заклёпок, что в итоге приводит к тому, что угловая скорость начинает падать. На левом моторе тоже можно заметить небольшие смещения красных дисков относительно заклёпок, но величина смещения значительно меньше, чем на правом моторе. Связано ли это с высокой угловой скоростью, или это результат неустойчивости вычислительной схемы, пока сказать трудно. Это не является целью данной статьи.
Теперь можно сделать выводы, которые лично для меня оказались неожиданными, если учитывать, что на некоторых форумах большие специалисты буквально категорически настаивают, что короткие, прямоугольные и высокоамплитудные импульсы с правильно подобранной фазой жизненно необходимы для, например, возбуждения колебаний в трансформаторе Тесла и аналогичных устройствах. И не только стараются убедить других в своей правоте, а буквально навязывают другим свою точку зрения. А любого, кто сомневается в их правоте, самым натуральным образом, обладая статусом модератора, выгоняют с форума, и закрывают к нему доступ.
Это для того, чтобы не мешал модератору и владельцу форума дурить доверчивую публику в течение нескольких лет, водить их по форуму, как Моисей водил евреев по Синайской пустыне.
Выводы:
17.03.2016.