Занявшись моделированием гравитационных двигателей в виде колёс Бесслера и Альдо Коста, а также параметрических маятников, пришлось столкнуться с тем, что каждый вариант гравитационного двигателя требует своего варианта параметрического возбуждения и поддержания вращения колёс или колебаний маятников.
Поэтому целью данной статьи является желание показать, в каких случаях выбрать тот или иной вариант управления параметрическим резонансом. Ибо всем известный вариант параметрического возбуждения физического маятника через управления моментом инерции так, как это принято в обычных качелях, оказался не единственным.
Чтобы все было наглядно, пришлось снова «собирать» модель, которая в некоторых случаях могла функционировать как колесо, а в других – как маятник.
Но при некоторых параметрах, такие как масса грузов или величина их зарядов даже обычный маятник начинал вести себя как колесо, то есть вращаться на все 360 градусов, причем направление вращение зависело от многих случайных факторов.
И если ставилась задача заставить маятник вращаться в конкретную сторону, то приходилось ему с самого начала задавать начальный толчок, чтобы он сразу с первой попытки смог совершить свой первый оборот в необходимую сторону. Обычно для этого достаточно было задать значение, направление и продолжительность силы, которую следовало наложить на маятник в момент запуска.
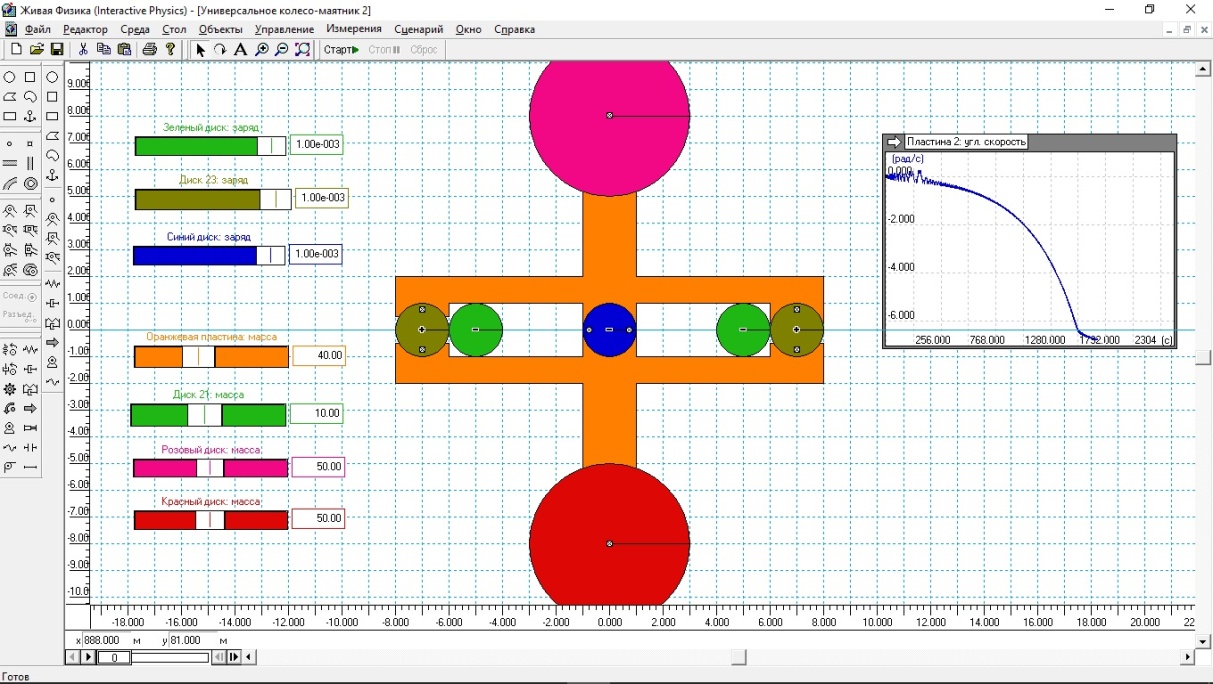
Итак, первая модель. (рис.1).

Рис.1.
Колесо на рис.1. имеет следующие параметры. Массы розового и красного диска по 50 кг каждый. Масса оранжевой пластины 40 кг. Масса каждого зеленого диска по 10 кг.
Для перемещения зеленых дисков используется электростатика.
Величина зарядов зеленных, бурых и синего диска составляют по модулю 1e-3 к. Знак заряда у синего диска отрицательный, а у бурых – положительный.
Начального толчка не потребовалось, так как в конструкции модели закралась незначительная асимметрия, что позволяет конструкции после запуска совершать колебания с небольшой амплитудой.
Чтобы обеспечить перемещение зеленных грузов величина и знак заряда их определялась по формуле:
if(body[21].p.y<0,Input[43],-input[43]) (1)
где body[21].p.y – Y-координата центра левого зеленного диска, у которого программа установила номер 21, input[43]- величина заряда левого зеленого диска, которая назначалась регулятором 43.
Формула указывает, что если Y-координата центра зеленого диска отрицательная, то заряд этого диска положительный, поэтому он будет притягиваться к синему диску и отталкиваться от бурого диска.
А если Y-координата положительная, то заряд зеленного диска становится отрицательным, он отталкивается от синего диска и притягивается к бурому диску. Соответственно, изменяется расстояние зеленого диска от оси вращения колеса.
То есть эта формула реализует алгоритм параметрического возбуждения колеса или маятника, который я называют алгоритмом Бесслера. Этот алгоритм простой, если центр подвижного зеленого диска оказывается выше оси вращения, то он отодвигается от оси вращения, а если центр зеленного диска оказывается ниже оси вращения, то он приближается к оси вращения.
В результате создается впечатление, что подвижные диски (грузы) смещаются противоестественным образом. После серии «толчков» колесо примерно на 300 секунде начинает вращаться по часовой стрелке, затем постепенно набирает по параболе угловую скорость, а примерно на 1800 секунде угловая скорость стабилизируется на 6.5 рад/с.
Достоинство данного способа параметрического возбуждения колеса в том, что перемещение зеленых грузов осуществляется вдоль горизонтали, на что требуется при прочих равных условиях меньше всего энергии.
И это достоинство дорого стоит, так превращает такое колесо, по сути, в вечный двигатель, так как такое колесо достаточно слегка раскачать, как дальше оно уже будет раскачиваться само, и, в конце концов, перейдёт во вращение.
Естественно, инженерам теперь предстоит огромная работа сконструировать простой внутренний механизм для перемещения грузов, используя в простейшем случае тросы, пружины и прочие мелочи.
Но можно использовать электромагниты, которые придется питать частью энергии, которую будет вырабатывать электрогенератор, подключенный к оси колеса.
Недостаток в том, что угловая скорость колеса возрастает медленно. Так что такое колесо нуждается в достаточной принудительной «раскрутке», чтобы колесо сразу вошло в режим вращения.
Теперь превратим наше колесо в маятник c примерно таким же моментом инерции, и посмотрим, как он будет вести себя в ответ на тот же вариант параметрического возбуждения (рис.2).
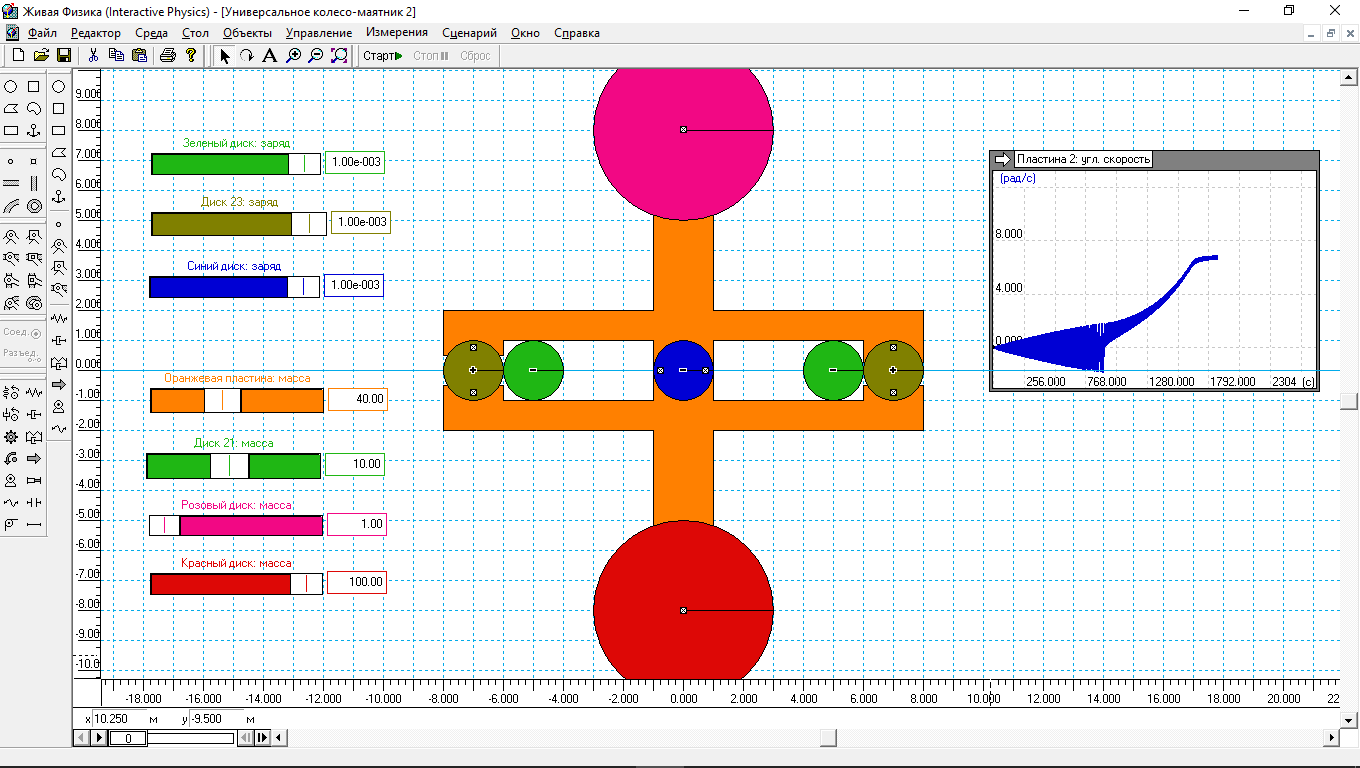
Рис.2.
Внешне вроде бы ничего не изменилось. Зеленые диски меняют свое положение по формуле (1). Но масса розового диска 1 кг, а красного – 100 кг.
Вместе это составляет 101 кг, примерно столько составляет сумма масс розового и красного диска на рис.1.
Там этот показатель равен 100 кг. Но теперь вместо колеса мы имеем маятник, но с примерно тем же моментом инерции относительно оси вращения.
Смотрим, как ведет такой маятник в ответ на тот же механизм параметрического возбуждения. Начальный период «раскрутки» этого маятника и превращение его в колесо отличатся от раскрутки колеса на рис.1.
Чтобы началось вращение, потребовалось почти 800 секунд. Но под конец колесо (маятник), наращивая обороты по параболе, стабилизировалось на угловой скорости в 6.5 рад/с.
Это показывает, что любое по форме колесо, но с тем же значением момента инерции, такими же по массе двумя зелеными дисками, и с теми же показателями по смещению к оси и от неё, приведут к близкой угловой скорости вращения колеса.
Поэтому этот маятник ничего не стоит замаскировать под колесо, или распределить 100 кг равномерно вдоль окружности, превратив, таким образом, маятник в настоящее колесо.
Теперь посмотрим, как будет себя вести маятник в перевернутом виде. Для этого установим с помощью регуляторов массу красного диска в 1 кг, а розового – в 100 кг. Результат моделирования на рис.3.
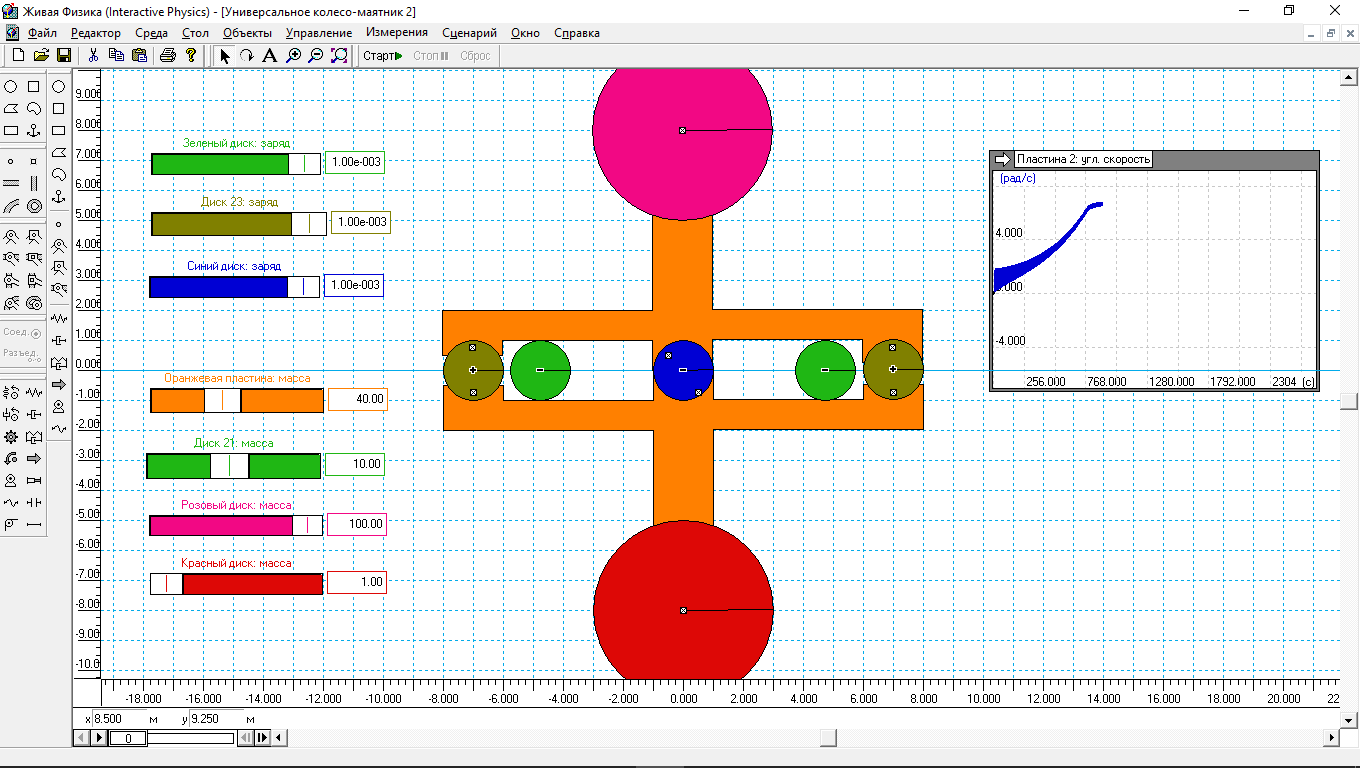
Рис.3.
На индикаторе справа показан результат. Период раскачки маятника отсутствует, маятник сразу переходит во вращение и на 800 секунде стабилизирует свою угловую скорость на уровне 7 рад/с.
Теперь немного изменим алгоритм, по которому будут смещаться зеленые диски. Примем, что положение их будет определяться направлением вектора скорости.
Если скорость бурого диска, соседнего с зеленым, направлена вверх, то зеленый диск смещается к оси, если скорость бурого диска направлена вниз, то зеленый диск смещается от оси.
Формула для знака заряда будет выглядеть так:
if(body[23].v.y<0,Input[43],-input[43]) (2)
где body[23].v.y – направление вектора скорости левого бурого, ближайшего к зеленому, диска, у которого программа установила номер 23, input[43]- величина заряда левого зеленого диска, которая назначается регулятором 43.
Вставлять в формулу (2) скорость зеленного диска нельзя, так как он под действием притяжения и отталкивания со стороны синего и бурого диска начинает вибрировать, что делает быстрое переключение диска из одной позиции в другую невозможным. Но перемещение происходит, хотя немного не так, как хотелось бы.
Формула указывает, что если скорость центра бурого диска отрицательная, то заряд соседнего зеленого диска положительный. Поэтому он будет притягиваться к синему диску и отталкиваться от бурого.
А если скорость бурого диска вдоль вертикали положительная, то заряд зеленного диска становится отрицательным. Он отталкивается от синего диска и притягивается к бурому диску. Соответственно, изменяется расстояние зеленого диска от оси вращения колеса.
Вот, что получается в результате моделирования (рис.4):
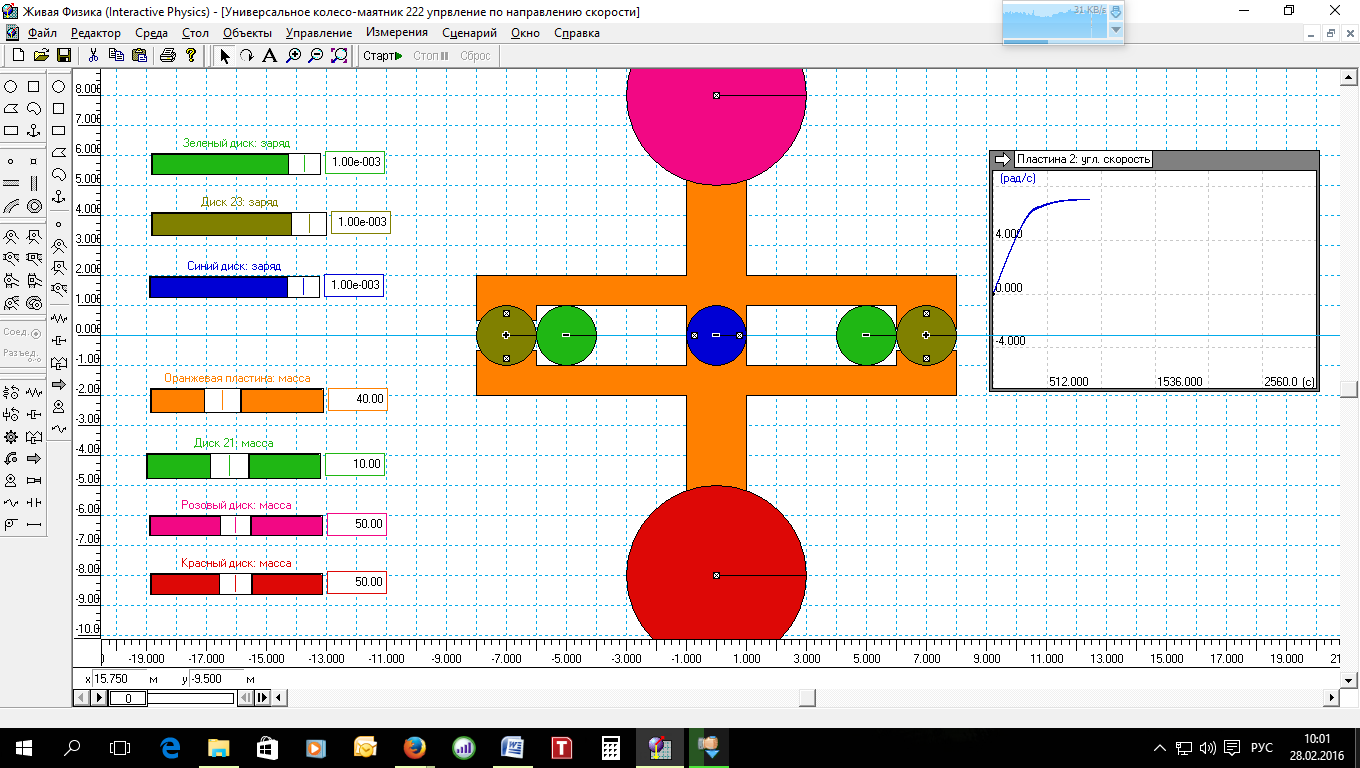
Рис.4.
Массы розового и красного дисков равны – 50 кг каждый. Результат моделирования можно увидеть на индикаторе справа. На нём видно, что колесо быстро набирает почти линейно угловую скорость, но затем угловая скорость стабилизируется на уровне 7 рад/с, что близко к раннее полученным значениям.
Это указывает на то, что максимальная скорость вращения колеса с заданным моментом инерции при прочих равных условиях не зависит от способа параметрического возбуждения. Так что при выборе варианта параметрического возбуждения следует руководствоваться простотой конструкции, которая будет перемещать зеленые грузы в нужном месте, в нужное время и в нужном направлении. Чем она будет проще, а еще лучше, если она будет требовать поменьше энергии, тем лучше. По своему поведению такое колесо сильно напоминает колесо Альдо Коста. Колесо Альдо Коста нельзя превратить в маятник. С другой стороны, колесо Альдо Коста вращается только в одну сторону, а колесо по алгоритму, отраженному в формуле (2), может вращаться в любую сторону, в какую его заставят принудительно вращаться.
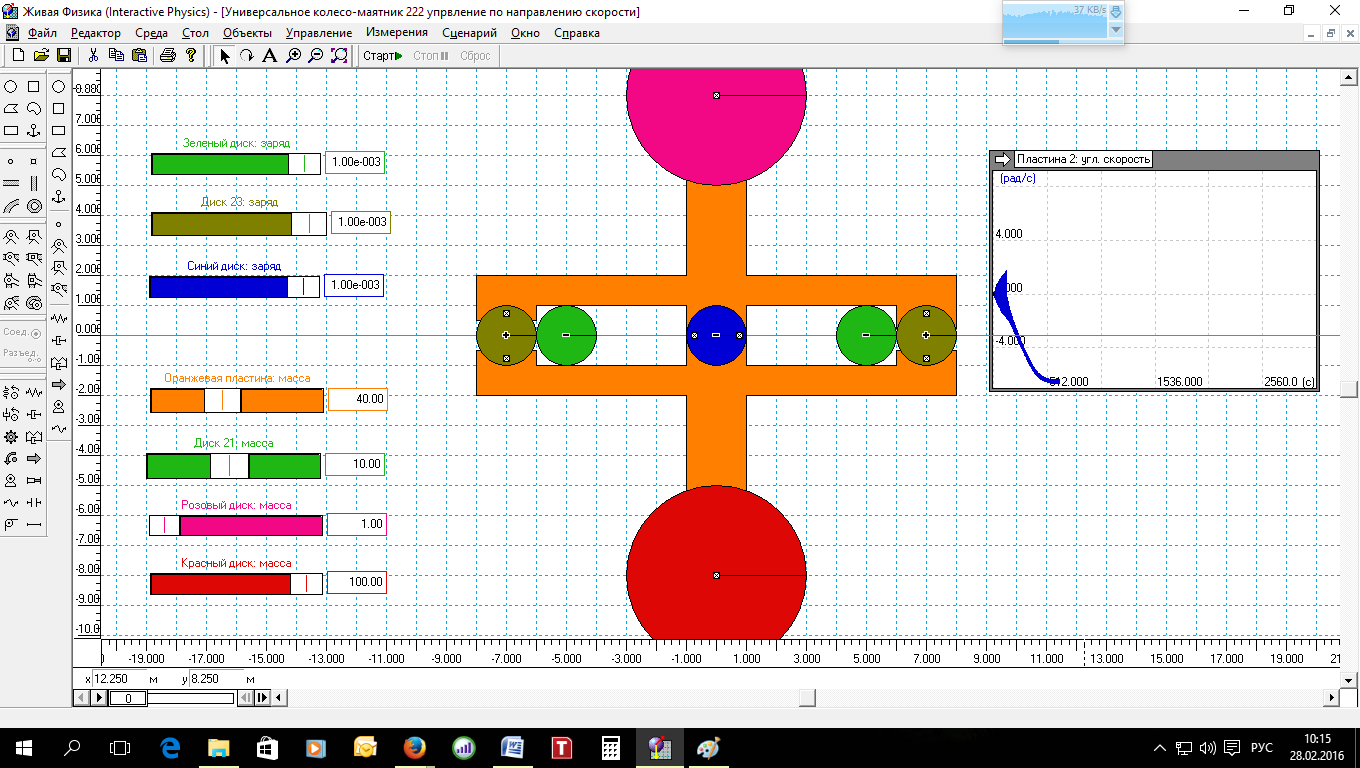
Рис.5.
Теперь проверим, что будет при том же способе параметрического возбуждения, если вместо колеса мы будем использовать маятник с тем же моментом инерции (рис.5).
Масса розового диска 1 кг, а красного 100 кг. Результат моделирования отражён на индикаторе справа. Маятник вначале раскачивается, а затем переходит во вращение. И достигает угловой скорости в 7 рад/с.
Теперь смоделируем колесо Альдо Коста. Вначале смоделируем вращение по часовой стрелке. Для этого заложим для заряда в зеленый диск следующую формулу:
if(body[21].p.x<0,Input[43],-input[43]) (3)
Где body[21].p.x – это X-координата зеленного диска 21. Input[43] – значение регулятора 43. Это самый верхний регулятор зелёного цвета.
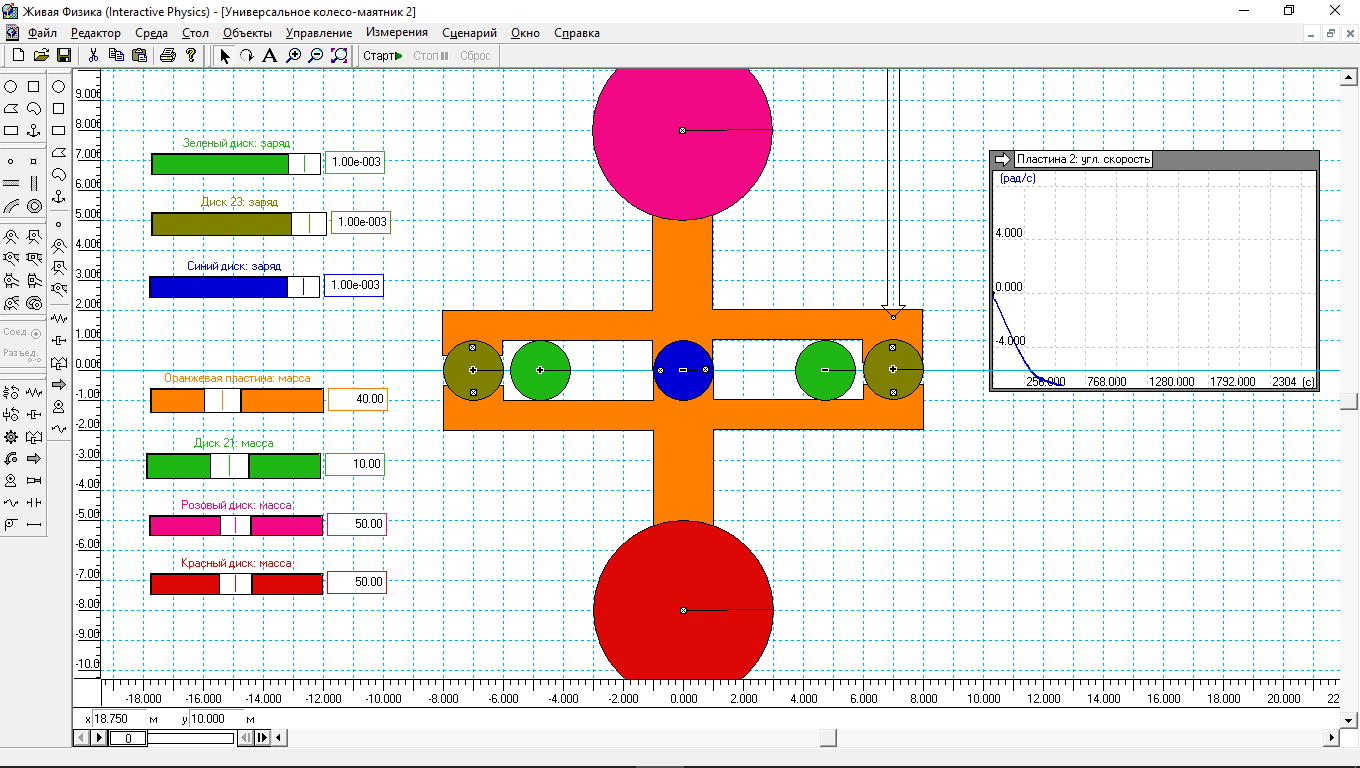
Рис.6.
Колесо ведет себя также как и прочие колеса Альдо Коста с односторонним вращением, промоделированные в других статьях. И очень похоже на колесо, которое показано на рис.4. Этот факт мы уже отметили, и поняли, что колесо на рис.4 может вращаться по одному и тому же алгоритму в любую сторону, а вот по формуле (3) колесо может вращаться только в одну сторону. Чтобы заставить колесо вращаться против часовой стрелки в формуле (3) знак неравенства “<” надо заменить на “>”.
Приводить результат моделирования не буду. И так всё ясно. Но такое моделирование проводилось. И оно подтвердило мои ожидания.
Так же замечено, что если в формулу, определяющую заряд подвижного зеленого диска входит скорость вдоль вертикальной оси, то система становится очень чувствительной к малейшим неровностям скорости перемещения зеленного груза по вертикали. Если же формула содержит только координаты по горизонтальной или вертикальной оси, то изменение знака заряда на противоположный знак происходит четче.
Это указывает на то, что устройство, обеспечивающее перемещение грузов вдоль радиуса колеса или маятника, прежде всего, должно опираться на пространственные координаты относительно оси колеса, как центра координат.
Если надо учитывать направление скорости «крыльев» колеса или маятника, то лучше опираться на скорости объектов, жестко закрепленных на колесе или маятнике на том же «радиусе, что и подвижный груз.
Итак, подведём некоторые итоги по моделированию гравитационных колёс и маятников. Можно сделать вывод, что вращением колеса можно управлять всего двумя подвижными грузами, главное, правильно подобрать их массу, определиться с алгоритмом перемещения в нужное время, в нужном месте и в нужном направлении. Даже можно использовать всего один подвижный диск. Остальная часть колеса может выглядеть как угодно.
Важно, чтобы колесо было сбалансированным относительно оси, проходящей через центр колеса перпендикулярно той линии, вдоль которой будет происходить перемещение подвижных грузов (подвижного груза). Этот показатель очень важен, так как он показывает, что два груза управляют вращением колеса, ось симметрии которого перпендикулярно перемещению управляющих грузов.
Это один из законов управления.
Максимальная угловая скорость вращения колеса, а также маятников, которые можно легко превратить в колесо, зависит при прочих равных условиях от центробежной силы, которая действует на подвижные грузы. Выбирая массу грузов, можно определиться с максимальной мощностью колеса, а также получить максимально возможную угловую скорость колеса.
С другой стороны, можно сконструировать при необходимости более мощную систему управления, чтобы она могла перемещать более массивные грузы, противодействуя центробежной силе. В моделях, подбирая величину зарядов, можно управлять максимальной угловой скоростью и мощностью колеса.
Теперь остается провести моделирование классического физического параметрического маятника, чтобы убедиться в том, как работает этот вариант параметрического резонанса и оценить его эффективность по сравнению с другими вариантами параметрического возбуждения гравитационных двигателей. Результат показан на рис.7.
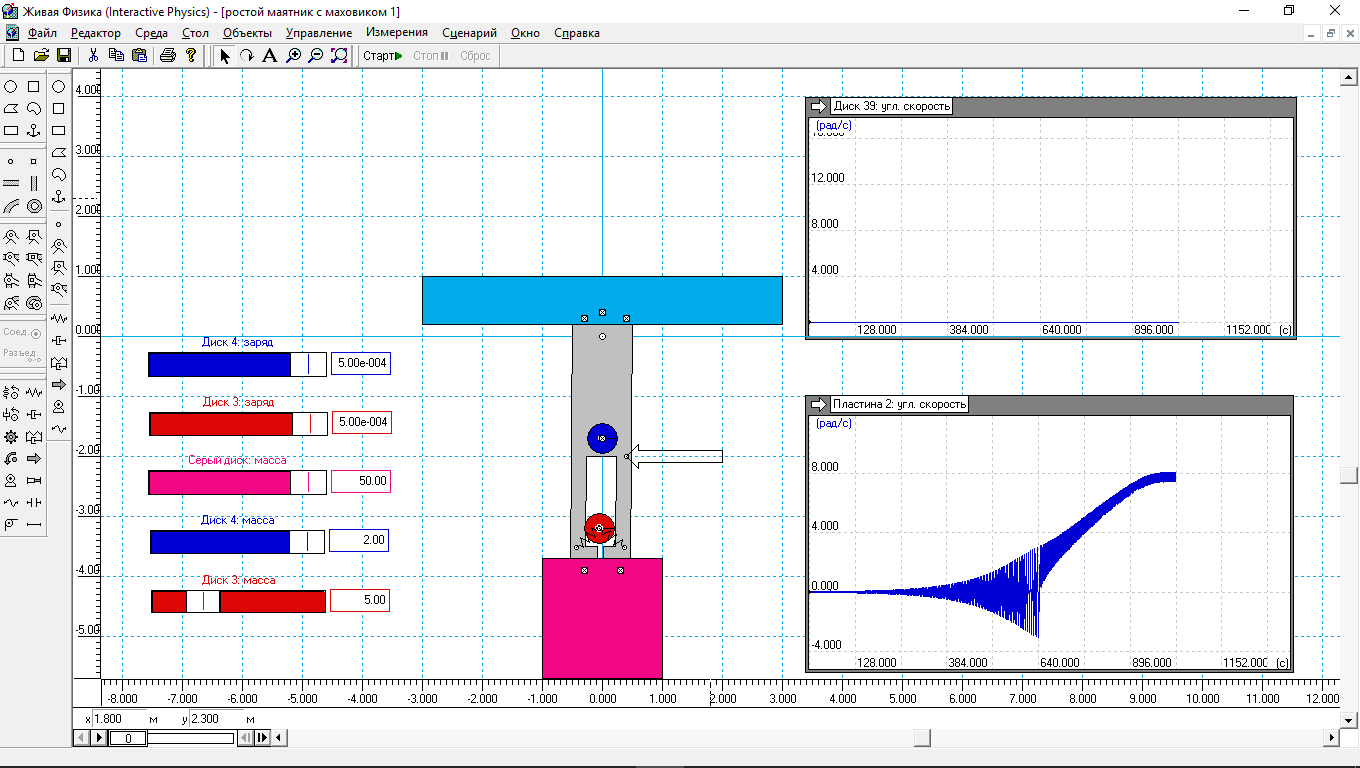
Рис.7.
Маятник – классический физический. В штоке проделана прорезь, вдоль которой может скользит красный груз, его заряд может изменяться по формуле:
if(body[3].p.x*body[2].v.r>=0,Input[13],-input[13]) (4)
где body[3].p.x – X- координата центра красного диска, body[2].v.r – угловая скорость серого штока маятника.
Приведенная формула обеспечивает движение красного груза при колебаниях маятника по траектории, которая похожа на восьмерку, но только с прямыми углами, такая траектория обеспечивает параметрический резонанс этого маятника.
И как показывает нижний справа индикатор, параметрический резонанс получается довольно эффективный. Максимальная угловая скорость – 8 рад/с. Красный груз массой в 5 кг, обеспечивает раскачку, а затем вращение маятника с общей массой в 112 кг.
Можете подсчитать сами. Масса розового квадрата – 50 кг, масса серого штока – 50 кг. Масса поперечной планки сверху – 5 кг. Масса синего диска 2 кг. И масса красного диска 5 кг. Итого 112 кг.
Можно применить формулу, где учитывается вектор скорости по вертикали.
Но снимать данные по скорости следует с соседнего с подвижным грузом объекта, который жестко закреплён на маятнике:
if(Body[16].v.y>0,Input[13],-input[13]) (5)
Где Body[16].v.y – вертикальная скорость центра розового квадрата (основной груз маятника). Результат моделирования примерно такой же, как и в случае применения формулы (4).
Максимальная угловая скорость маятника, когда он вращается на 360 градусов, примерно равна 8 рад/с. Так что формулы (4) и (5) приводят к одинаковому результату, но формула (5) проще.
На этом знакомство с результатами моделирования можно закончить, так как реально в «Живой физике» можно собрать великое множество моделей, но нам важно получить ответы на поставленные вопросы. И мы их получили.
Проверили несколько алгоритмов, по которым можно осуществлять перемещение подвижных грузов (и даже одного подвижного груза).
Все они оказались рабочими, все они доводили маятники и колёса до предельной угловой скорости, которая определялась центробежной силой, какой уже не могла противодействовать принятая в наших условиях электростатическая сила.
В реальных параметрических маятниках и колесах, естественно, придется использовать совершенно другой механизм перемещения подвижных дисков.
Чтобы они были простыми и не требовали больших энергетических затрат, что должно оцениваться по соотношению затрат на управление параметрическим резонансом и энергией, которую можно будет снять с вала колеса или маятника.
Естественно, обязательно найдутся противники вечных двигателей, которые будут утверждать, что энергия маятника подпитывается устройством, которое будет обеспечивать перемещение подвижных дисков (в данном случае красного диска). Но масса красного диска 5 кг, а масса маятника 112 кг.
Кроме того, угловая скорость маятника постоянно нарастает. И эту энергию можно вычислить по формуле:
E = J*w^2/2 (6)
Где E – энергия вращения, J- момент инерции маятника, w – частота вращения маятника (колеса).
Если даже принять, что энергия вращения маятника (колеса) растет порциями от оборота, к обороту, то тогда почему энергия вращения маятника (колеса) растет пропорционально квадрату частоты вращения.
Ведь по графику на индикаторе видно, что частота растет линейно. А должна расти по обратной параболе второй степени – корню квадратному от добавляемой порции энергии, которая, якобы, одинакова от оборота к обороту.
Если быть более серьёзным, то сморите. В крайних положениях у любого маятника угловая скорость равна нулю. Поэтому там при перемещении подвижного груза изменяется только потенциальная энергия всего маятника и груза. И если угол оклонения равен 90 градусов, то потенциальная энергия не изменяется. А положение подвижного груза меняется очень заметно, изменяя момент инерции и сил, они заметно возрастают. Если подвижный груз перемещается от перефирии к центру на некую высоту в тот момент, когда маятник занимает вертикальное положение, то система, смещающая груз, выполянет работу против суммы сил - силы тяжести и центробежной силы. Последняя же изменяется крайне нелинейно. Совершёная системой управления по перемещению груза работа переходит в кинетическую энергию маятника, точнее энергию вращения. При этом энергия вращения меняется пропорционально разности квадратов радиусов R^2-r^2, где R - это масимальный радиус, а r - это минимальный радиус относительно оси вращения маятника. То есть изменение энергии вращения маятника подчиняется нелинейной функции. Вот это указывает на то, что энергия качающегося маятника растёт быстрее той энергии, которая поступает в неё от задающего генератора в виде двух подвижных грузов и подсистемы, которая их перемещает в нужном месте, в нужное время и в нужном направлении.
Значит энергия вращающегося маятника (колеса) растет быстрее, чем добавляется в неё за счет работы системы управления перемещением груза, за счет чего обеспечивается параметрический резонанс.
Так что даже на таком простом примере мы имеем вживую вечное движение, а значит вечный двигатель. Сделаю оговорку, это не вечный двигатель, а усилитель мощности, мощностью которого можно управлять очень простым способом.
Надо только найти способ частью полученной от вращения маятника (колеса) энергии обеспечить работу системы управления параметрическим резонансом, которая в нужный момент времени, в нужном месте и в нужном направлении обеспечит перемещение подвижных грузов.
Кто не верит, тот пусть считает. Или делает колесо своими руками.
Теперь соединим этот маятник с маховиком. Рис.8.
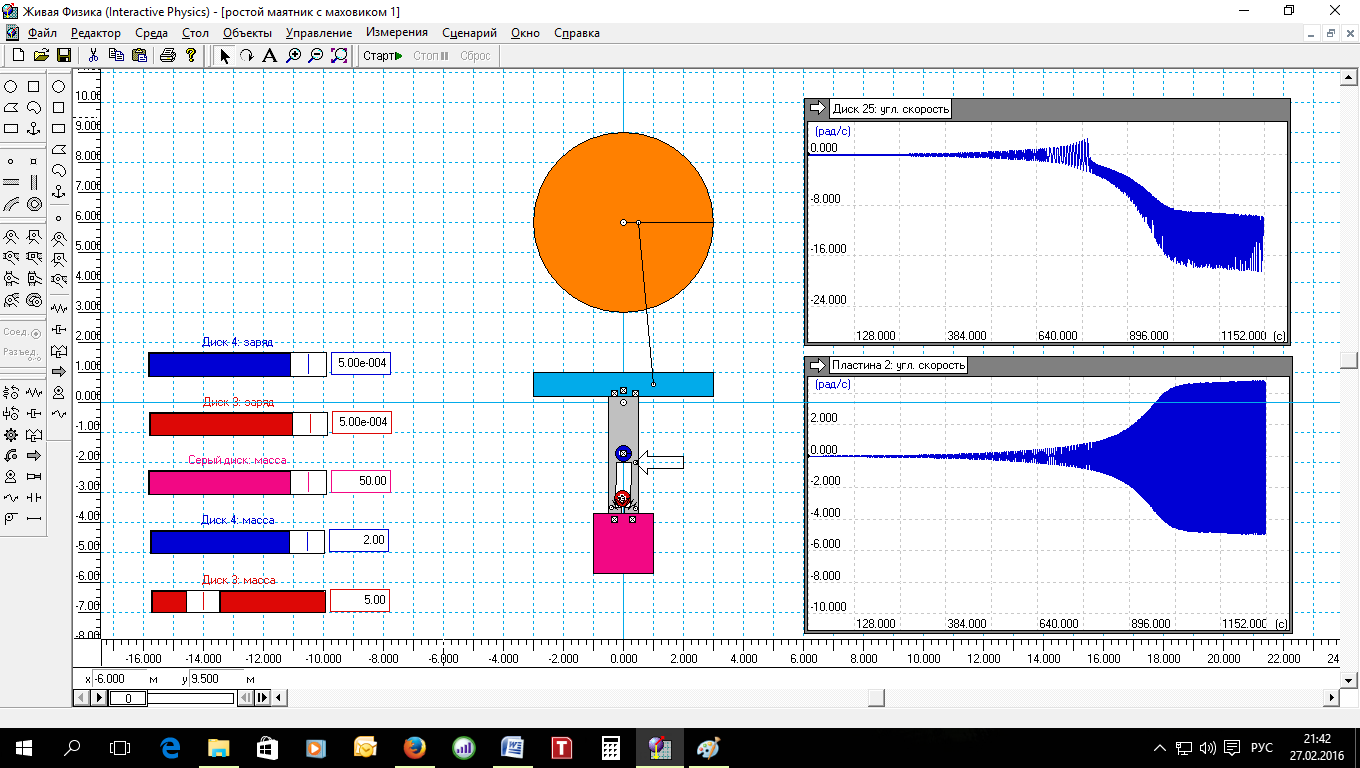
Рис.8.
На скане окна программы «Живая физика» уже рассмотренный выше маятник подсоединён к маховику (колесу) оранжевого цвета. Диаметр колеса около 5 м. Индикаторы справа от маятника с колесом показывают, что на 760 секунде маятник раскачался до того, что оранжевый маховик начал вращаться по часовой стрелке. При этом частота колебаний и угловая скорость колеса нарастали по сложной кривой до конца эксперимента. Время можно увидеть на индикаторе.
По графикам на индикаторах ясно, что секунд через 500 в системе амплитуда колебаний и угловая скорость вращения колеса расти перестаёт, но итоговые показатели впечатляют. Максимальная угловая скорость маятника около 5 рад/в, а колеса – минимум 18 рад/с.
Проанализировав поведение нескольких моделей колес и маятников, естественно, следует задать простой вопрос – откуда берется дополнительная энергия? Попробуем ответить на него.
Параметрический маятник является замечательным примером того, как организовать некий мощный колебательный процесс с помощью другого колебательного процесса меньшей мощности и направленного перпендикулярно главному процессу. А перпендикулярность процессов, а точнее потоков энергии - это главный признак того, что маломощный процесс управляет мощным процессом, и одновременно запитывается от него напрямую или через вспомогательные устройства.
Что касается того, откуда энергия берется, то можно сказать, что ниоткуда. Ибо в любом колебательном процессе есть положительные энергетические потоки, и потоки отрицательные, что в сумме по целому числу периодов дает энергетический ноль. Но человек от этих колебаний берет крошечную часть энергии, выпрямляет её и использует. В дальнейшем он может отработанную энергию выбросить в окружающую среду, где она постепенно рассосётся и обнулится, или перейдет в другие формы энергии.
Это же касается и управляющего осциллятора. Его энергия тоже в сумме за некое число полных периодов практически равна нулю. Так что и тут полный ноль.
Вывод. Любая энергия ни откуда не берется, и никуда не исчезает. И то, что мы называем потоками энергии - это только жалкая часть из половины тех потоков, которые перемещаются туда и сюда, или вращаются в эфире. Но они не проявляют себя, так как все потоки эфира, какими бы мощными не были, имеют своего двойника, который движется в противоположном направлении. Любой вихрь всегда имеет парный вихрь, но с противоположным направлением вращения. И т.д. То есть, Природа очень экономна в энергетическом отношении. И она использует только те энергетические потоки, в которых у неё имеется острая необходимость. Природа, как любой настоящий хищник, лишнее не употребляет. Но если Природе необходим какой-то объем энергии, то она его создает буквально из ничего, закручивая сразу два потока, один использует, а другой заставляет превратиться в другие виды энергии. Но чаще использует сразу два вихря или два потока, в сумме дающих энергетический ноль.
Надо и людям не только уметь извлекать энергию из существующих природных потоков, но и создавать вихри из стоячего эфира, любой подходящей среды – воздуха, воды и т.д. И использовать энергию либо обоих вихрей сразу, или только одного, а энергию второго оставить на усмотрение природы (самого эфира). И создать с нуля два вихря в эфире или иной среде можно только с помощью параметрического резонанса.
Физики пока еще этого в полной мере не понимают. Они рассматривают параметрический резонанс только на уровне игрушек. А это похоже на то же самое, что было в Центральной Америке, где до прихода европейцев аборигены знали колесо, но боги разрешали делать из них игрушки, а взрослым использовать колёса запрещали, и заставляли индейцев ходить пешком. Поэтому в то время, когда Европейцы широко использовали водяные и ветряные мельницы, а также парусные корабли, в Центральной Америке люди ели друг друга, питаясь энергией друг друга самым непосредственным образом, ничем не отличаясь в этом отношении от животных. Думаю, что это был особый эксперимент неких сил, которые создали людей в Южной и Центральной Америке или собрали их в мощные государства, а затем проверили эти государства на прочность, столкнув их с цивилизацией Европы. Результат всем известен – цивилизация колёс и парусных кораблей победила цивилизацию голых рук и ног.
Параметрические колебания можно возбудить только в системе, которая находится под давлением, напряжением или иным постоянным силовым воздействием, как природного (атмосфера, электростатическое поле Земли, гравитационное поле Земли, подводный мир и т.д.), так и рукотворного характера (воздушный пузырь в бочке с водой, мешок картошки или домкрат).
Так что при параметрических колебаниях не надо ставить вопрос – откуда энергия. Энергия поступает из окружающего пространства благодаря правильно организованному колебательному процессу. И минимум половина этой энергии может оказаться в распоряжении людей. Давайте внимательно присмотримся к тому, что происходит на рис.7. Ведь там маятник совершает колебания под управлением параметрического резонанса. Эти колебания, если их оставить как есть, никакой пользы нам не принесут. Энергию нужно снять с маятника. И для этого используется механический выпрямитель в виде поперечной планки наверху маятника, и прута, которые вместе превращают колебания маятника во вращение оранжевого маховика строго в одну сторону. Конечно, сразу это не получается, приходится раскачивать маятник. Но после того, как маятник начинает вращать колесо в одну сторону, приходится только и делать, что отводить энергию в нагрузку. Иначе напор энергии обязательно разорвет маховик и сломает маятник. На это указывает все нарастающая угловая скорость как маятника, так и колеса.
Если сравнивать данную механическую систему с электронной системой, то сразу вспоминается вилка Авраменко. Там тоже энергия появляется из ничего, переносится по одному проводу, а затем подключается к нагрузке с помощью двух диодов.
Параметрические колебания отличаются от простых колебаний тем, что колебания простых колебаний, как правило, стабильны по частоте, а вот колебания системы при параметрическом резонансе нарастают как по частоте, так и по амплитуде. Что при непринятии мер по отводу энергии в некую нагрузку обязательно приведет к разрушению системы. Либо надо менять главные параметры системы, от которых зависит интенсивность параметрического резонанса.
Вот сейчас кризис в России усиливает самые разные колебания в финансах, экономике, социальных отношениях и т.д. Это указывает на то, что некие силы запустили по всему миру параметрический резонанс, и смотрят, что из этого получится. Но правительства практически всех государств ведут себя как слепые котята. Ведут себя как кролик перед удавом. Кролик понимает, что будет проглочен, но ничего уже сделать не может. Можно облить удава кипятком, но это надо делать уже не кролику, а кому-то другому. Вот этого другого помощника у человечества, похоже, нет. Люди надеются на бога, но не на себя. Человечество спокойно ждёт, когда некие силы с помощью кризиса начнут заглатывать страну за страной, в надежде, что после гибели конкурента спасшийся сможет уцелеть. Наивная простота… Выжившие в этой мясорубке будут завидовать мертвым. Такие они, к сожалению, люди. Пляшут до самого последней минуты своей жизни, а надо браться за метлу и лопату, чтобы разгрести накопившейся навоз. Где же ты, наш Геркулес? Нет больше Геркулеса!!! Люди, проснитесь!!! Цунами уже под нашими окнами!!!
Вот, что такое параметрический резонанс. Если с ним правильно обращаться, то он может одарить нас энергией. Но стоит зазеваться, как рушатся мосты, здания, государства и весь мир. Ибо всё, что находится под напряжением, давлением, иным мощным силовым воздействием, в любой момент могут разрушиться, если тем или иным способом организовать параметрический резонанс, который по своим разрушительным последствиям опаснее простого резонанса в десятки и сотни раз. Не зря Тесла заявлял, что он может легко расколоть Земной Шар. Ибо простой резонанс только преобразует поступающую энергию, если частота воздействия близка к собственной частоте системы. И поэтому энергия простого резонанса не может быть выше той энергии, которая поступает в систему. А вот параметрический резонанс высвобождает энергию, которая заключена в окружающем пространстве самим силовым полем. Причем, выбрасывая эту энергию, некоторые поля имеют возможность восстановить самостоятельно свою мощность из окружающего нас пространства. И тем самым снова среагировать аналогичным образом на повторный параметрический резонанс, превращаясь в вечные источники энергии.
Чтобы резонанс стал параметрическим, следует поддерживать частоту колебания задающего генератора в два раза выше частоты колебаний системы, которую мы будем раскачивать. А это значит, что частоту колебаний задающего генератора придется постоянно синхронизировать с частотой колебаний раскачиваемой системы. В рассмотренных в данной статье моделях маятников и колес это правило соблюдалось автоматически, то есть эти системы обладают свойством самофазировки и самосинхронизации.
Вот почему гравитационные колеса, как гравитационные двигатели, будут вращаться благодаря параметрическому резонансу до тех пор, пока не разрушится наша Земля. Но с другой стороны бояться, что гравитационные двигатели разрушат Землю, не надо. Ибо сделать это они не смогут никогда, если в них изначально заложить некие ограничители. Землю могут разрушить только дураки, занимающие высокие государственные посты, кто имеет право отдать приказ нанести по Земле ядерный или термоядерный удар. А простая гравитационная силовая установка позволит нам получать энергию и только всего. И нам, вообще, больше и не надо. Нам нужна энергия не для разрушения, а для жизни и созидания.
28.02.2016