Всем известно, как легко раскачивать качели, даже для взрослых, если их в такт подталкивать небольшими усилиями в момент прохождения качелей самой нижней точки своей траектории. Это умеют делать как взрослые, так и дети. Видимо это неспроста.
Поэтому возникла идея провести моделирование простых качелей, раскачиваемых простым подталкиванием (сила направлена в сторону движения качелей) один или два раза в течении одного периода колебаний. Размышление над этой темой привели меня к мысли, что маятник Челкалиса – это самые обыкновенные «взрослые» качели, превращенные в колесо с помощью правильного запуска и в последующем правильного параметрического возбуждения с помощью воздействия на дугу (сегмент) маятника с помощью двух небольших, но быстро вращающихся колёс с шинами и резиновыми камерами внутри.
Когда дуга маятника проходит между вращающимися колесами, то камеры с воздухом сжимаются и зажимают шинами между собой участок сегмента маятника, а затем эти же колеса выбрасывают сегмент маятника с огромной силой, увеличивая тем самым энергию маятника. И тут важно не только применение колес с шинами и камерами, но и тот факт, что коэффициент трения покоя и скольжения между железом и резиной составляет более 0.8. То есть сила трения практически равна силе давления, с которой малые колеса прижимаются к дуге маятника. Чем больше «прижим», тем с большей силой «выстреливается» маятник из «объятий» колёс. И если эти 2подгоняющих» сил достаточно, чтобы преодолеть сопротивление на валу маятника, то остается мощность, которую можно передать в нагрузку.
При этом, для формирования «подгоняемых» сил затраты энергии могут оказаться значительно меньше той энергии, которую можно снять с вала маятника Челкалиса. Он же – взрослые качели особой конструкции.
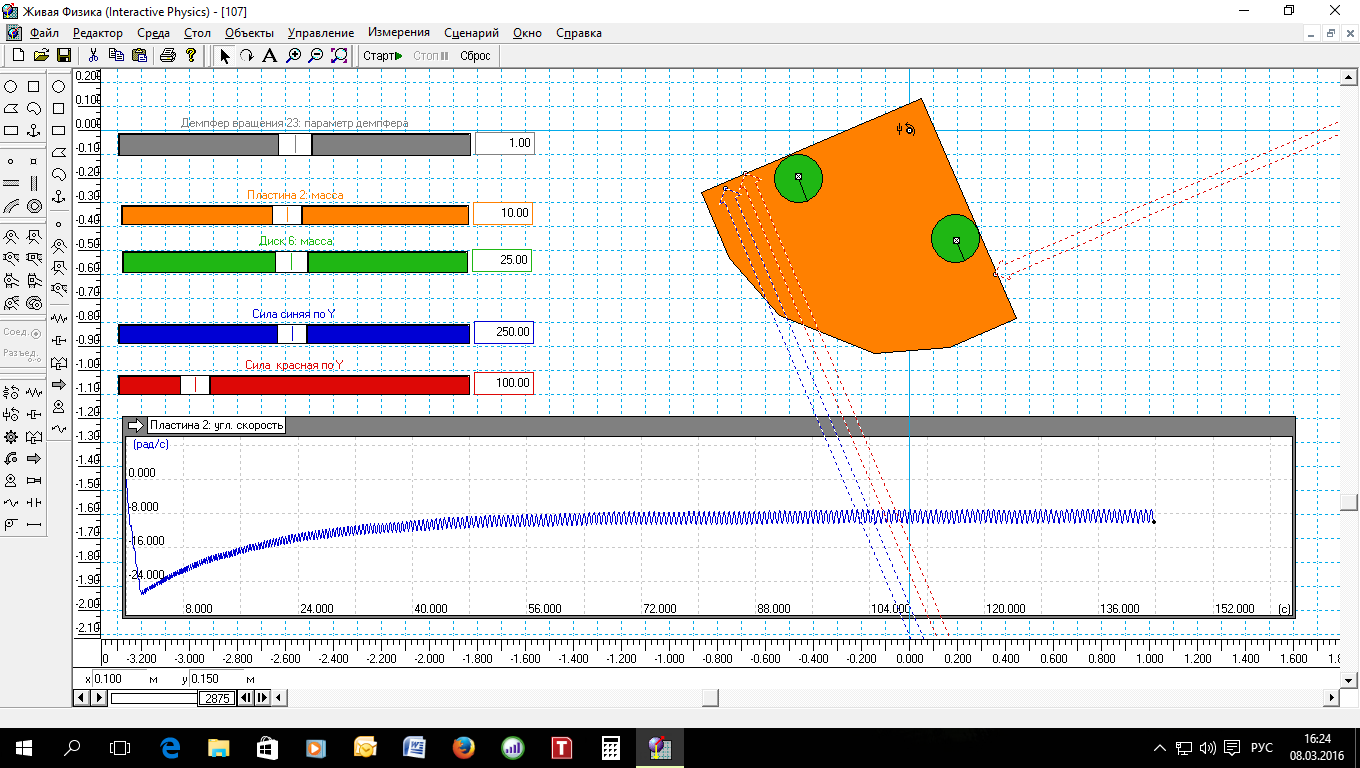
На рис.1. показана модель и результата моделирования.

Рис.1. Результат моделирования маятника Челкалиса.
«Снимок» экрана сделан в после временной остановки моделирования. А после нажатия кнопки «Сброс» картина уже выглядит так (рис.2).
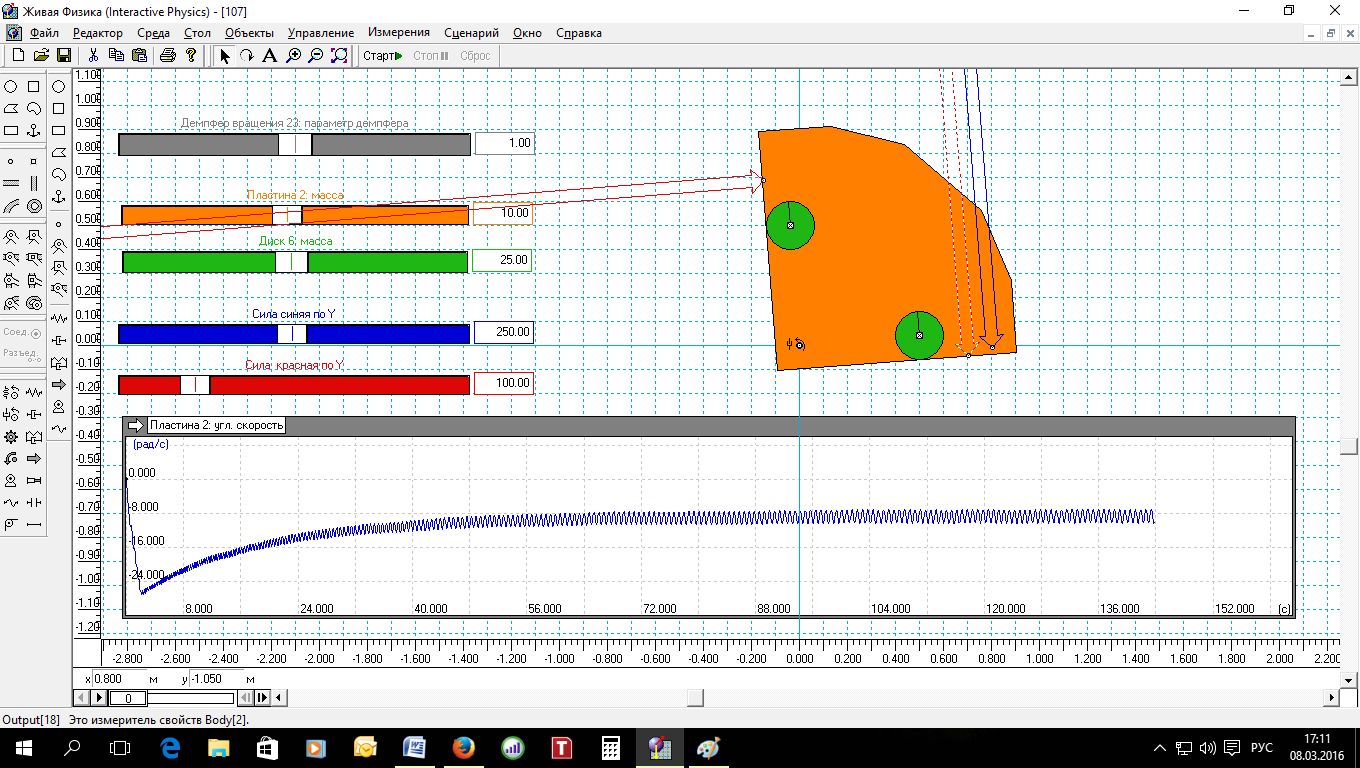
Рис.2. Модель маятника Челкалиса в начальном состоянии и индикатором с результатом моделирования.
Попробуем теперь разобраться, из чего состоит наша модель. Модель простая. В принципе в качестве соновы для маятника можно было взять диск, но решено было максимально приблизиться к форме маятника Челкалиса. Поэтому была использована пластина, близкая по форме к четверти круга. Масса пластины определяется оранжевым регулятором и в данном случае масса пластины равна 10 кг. Радиус у пластины примерно 90 см. Зеленные диски моделируют грузы (противовесы), масса каждого диска определяется зеленым регулятором, и в данном случае масса каждого зеленого диска составляет 25 кг.
На ось маятника «посажен» демпфер, параметры которого определяются серым регулятором. Размерность демпфирования н*м*с/рад. С помощью изменения параметров демпфера можно задавать некий момент, который можно рассматривать как некое сопротивление, преодоление которого обеспечит раскачку маятника до некой угловой скорости. Кроме того, наличие демпфера обеспечивает невозможность маятника пойти в «разнос». Для эксперимента у демпфера был установлен показатель 1 н*м*с/рад. Но можно менять этот показатель с 0 до 2 н*м*с/рад. Причём по ходу эксперимента.
Для ритмичного подталкивания маятника были введены две силы. На рис.1 и 2 эти силы обозначены красным цветом. Причём действуют эти силы не всегда, а только тогда, когда синус угла поворота маятника меньше 0.1. Это условие было в виде формулы введено в основной параметр красных сил (рс.3).

Рис.3
Величина силы, когда она существует определяется регулятором input[24] красного цвета. А моменты времени, когда эта сила существует, определяется формулой:
if(abs(sin(body[2].p.r))<0.1,1,0) (1)
У второй силы, которая перпендикулярна первой, критерий для существования немного другой:
if(abs(sin(body[2].p.r+pi()/2))<0.1,1,0) (2)
Эти показывает, что между периодами существования красных сил существует фаза, равная 90 градусов. Сами же силы появляются тогда, когда синус угла поворота маятника (оранжевая пластина) меньше 0.1. А это будет наблюдаться 2 раза за один оборот маятника. Величина красных сил равна 100 н.
На индикаторе внизу окна программы видно, что в течении первых двух секунд происходит начальная «раскрутка» маятника, чтобы он гарантировано начал вращаться в одну сторону против часовой стрелки. Для этого в течении этих двух секунд действует синяя сила, величина которой определяется синим регулятором. В данном случае величина синей силы равна 250 н.
Во время начальной «раскрутки» вначале угловая скорость увеличивается почти линейно до 26 рад/с. Но затем угловая скорость уменьшается по логарифмической кривой и «устаканивается» на уровне 8 рад/с.
Во время эксперимента можно менять все параметры, которые «вынесены» на регуляторы. По идее можно связать с регуляторами все параметры, от которых так или иначе зависит поведение маятника Челкалиса. Но это уже на усмотрение читателей.
Так же на усмотрение читателей я пока оставляю оценку мощностных показателей – мощность маятника во время вращения и мощность, которую развивают красные силы. Сравнение этих средних показателей позволило бы сделать вывод о целесообразности использования маятника Челкалиса в качестве СЕ генератора. Возможно, я тоже этим займусь. И не только в отношении маятника Челкалиса, но и в отношении всех раннее рассмотренных моделей.
Маятник Челкалиса – это удобный объект, на котором можно изучать законы параметрического резонанса. Это тема отдельного исследования. А пока могу сделать вывод, что маятник Челкалиса подтверждает результаты наблюдения за поведением других моделей – как колёс, так и маятников. Первый вывод – зависимость угловой скорости маятника от энергии вращения. Чем с большей частотой вращается маятник, тем выше энергия вращения. То есть, частота колебаний параметрической системы по мере накачки её энергией всё сильнее и сильнее отличается от частоты свободных колебаний системы, когда параметрической накачки нет.
Второй вывод – это необходимость соблюдения соотношения между частотой колебаний параметрической системы и параметрического задающего генератора. Если система колеблется на частоте ?, то задающий генератор должен работать на частоте 2?. Главной проблемой параметрических систем является не это, а необходимость поддерживать это соотношение автоматически. И тут следует заметить, что у параметрических колёс и маятников это условие реализовать очень легко, гораздо проще, чем в электротехнических или электронных устройствах.
В частности, у маятника Челкалиса сама конструкция обеспечивает автоматически соблюдение этого важнейшего условия параметрического резонанса. Правда, в настоящей конструкции «подталкивающая» сила «оживает» на один оборот маятника всего 1 раз. Но синхронность эта соблюдается при любой частоте вращения маятника. Кроме того, у настоящего маятника Челкалиса, маятник «подгоняют» две силы, разнесенные во времени на 60 градусов. Вначале подталкивает одна сила, а через 1/6 оборота – вторая.
Еще один важный вывод, который удалось получить от моделирования маятника Челкалиса, так это то, что силовое воздействие типа подталкивания по ходу перемещения маятника является наиболее простым и энергетически, наверное, выгодным вариантом параметрического резонанса. Нет необходимости изменять массу или момент инерции частей колебательной системы. Надо только найти источник «подгоняющей силы» и обеспечить, чтобы она действовала в нужном месте, нужном направлении и в течении заданного интервала времени. И при этом могла еще менять свое значение по модулю. Для механических систем типа маятника или колеса сделать это не составит большого труда. Да и силу можно получать самым разным способом – электростатика, магниты, пар, струя газа или плазмы, механические лопасти, вращаемые истоником энергии и т.д.
Давайте качественно оценим импульсное силовое воздействие на энергию маятника. Пусть масса подталкиваемого маятника равна m, а скорость её в момент подталкивания v. Тогда импульс равен m*v, а кинетическая энергия – m*v*v/2. Если мы подтолкнем маятник силой F в течении интервала времени ?t, то получим импульс, равны F* ?t.
Значит, после «подталкивания» импульс маятника станет равным m*v+F* ?t. Но при этом кинетическая энергия станет равной m*(v+F* ?t/m)* (v+F* ?t/m)/2. Это показывает, что импульс маятника после подталкивания увеличивается линейно, а кинетическая энергия растёт по кривой второй степени. И если mv>>F* ?t, то вклад силы в увеличение энергии незначительный, но если mv<<F* ?t, то основная добавка к энергии будет определяться импульсом силы – величной силы и длительностью её воздействия на маятник. А если еще учесть, что F* ?t*L, где L – это плечо, расстояние точки воздействия силы от оси маятника, то понятно, что чем больше это плечо, тем сильнее будет воздействие импульса силы на энергию системы. Так что явная нелинейность маятника Челкалиса позволяет надеяться, что перед нами сверхъединичное устройство. И задача тех, кто будет собирать такой маятник, состоит в том, чтобы в момент контакта «низа» маятника с «подталкивающими» колесами, формируемая сила была как можно больше. Но маятник можно подталкивать и иным способом.
Сравнивая такие системы как колесо Дмитриева, колесо Бесслера, колесо Альдо Коста, маятник Челкалиса и массу параметрических маятников разной конструкции, прихожу к выводу, что все эти системы объединяет параметрический резонанс, несмотря на то, что он организован у разных авторов по разному. Поэтому я не вижу причин для спора между Челкалисом и Дмитриевым. Параметрический резонанс есть у обоих изобретений а вот реализован он по-разному.
Подведем итог. Маятник Челкалиса – это параметрическая система, которая «раскачивается» импульсами сил, которые создаются в результате взаимодействия маятника и вспомогательных колес с пневматикой. И такой системой очень просто управлять, чтобы сделать её в будущем интересным источником энергии. Стало понятно, что в основе маятника Челкалиса лежат самые обычные качели, которыми привыкли баловаться на Руси.
06.03.2016