
Власов В.Н.
vitanar@yandex.ru
Очередное моделирование инерцоидов в программе «Живая физика»
Вступление.
Программа «Живая физика» позволяет, не отрываясь от компьютерного стола, проверить некоторые идеи, на реализацию которых в иных условиях могут уйти годы и огромные деньги. Используя данную программу в 2019 году, я написал три статьи о моделировании разных инерцоидов, в том числе и инерцоидов Толчина. Для меня эти статьи стали важным этапом в моей жизни. Они позволили понять роль центробежных сил, как в теории, так и практике инерцоидов. Заодно отвлекли меня от грустных мыслей, когда жизнь моя висела на волоске.
Прошло почти 6 лет, появились новые данные. Захотелось вновь проверить новые идеи, заодно убедиться, что навыки работы с «Живой физикой» ещё не потеряны. В предыдущей статье я попытался разобраться с некоторыми соображениями, которые возникли у меня при изучении поведении параметрического маятника. Стало понятно, что параметрический маятник можно использовать в качестве безтопливного генератора. Решил проверить ещё один параметрический маятник, в котором груз на пруте с переменной длиной вращается по эллипсу, с большой горизонтальной осью и малой вертикальной осью. Оказалось, что и он прекрасно вращается вокруг оси вращения. Правда, раскачивался долго, но после показал высший пилотаж.
Поэтому представляю свои новые находки читателям. Делаю это не просто так, а в надежде, что некоторым читателям из проработанных моделей что-то понравится, и они сотворят из них, например, мощный безтопливный генератор энергии. Инерцоиды – это не игрушки, это будущее нашего мира.
Основная цель всех моих виртуальных экспериментов в программе «Живая физика» - понять, как повысить эффективность центробежных инерцоидов, а с другой стороны понять особенности инерцоида В.Толчина.
Дело в том, что простая на вид игрушка таит в себе множество загадок. И когда начинаешь их разгадывать, снимая один слой загадок за другими, то возникает желание рубануть по инерцоиду Толчина мечом Александра Македонского. Есть побочные эффекты более глубоких законов природы, до которых наш разум ещё не дошёл.
Конечно, можно привлёчь к изучению ОТО Альберта Эйнштейна, или поверить в 4-D гироскоп Г.И.Шипова. Но с другой стороны скорости в инерцоиде Толчина далеки от световых, а размеры инерцоида В.Толчина не такие уж большие, чтобы привлекать к изучению мощные вихревые эфирные процессы. По сути, учёные не понимают, почему удаётся ездить на велосипеде, да и само велосипедное колесо практически не изучено как маховик или гироскоп. Да и продольная инерция практически не изучается
Ездить на велосипеде у всех получается, а вот почему это возможно, учёные точного ответа не дают. Уверен, что у велосипеда множество скрытых возможностей. Похоже, что из любого велосипеда можно сделать, например, маятник (БТГ) Челкалиса. И зимой он будет отапливать дом.
Так и с инерцоидом Толчина. Вдруг выяснится такое, что волосы на голове дыбом встанут. А пока приступим к анализу результатов экспериментов в программе «Живая физика».
Модель первая.

Рис.1
Это модель простого вибратора. На основании голубого цвета установлены два маховика алого цвета с дебалансами зелёного цвета. Основание имеет массу 100 кг, алые маховики имеют массу по 5 кг, у дебалансов масса по 25 кг. Сама модель расположена в верхней части рисунка. На оси каждого алого маховика установлен мотор, угловая скорость которых составляет 1 рад/с. Верхний маховик вращается по часовой стрелке, нижний – против.. В результате вся конструкция получает нулевой момент вращения.
В нижней части рисунка размещается индикатор, который показывает ускорение (зелёная синусоида), скорость (красная синусоида) и пройденный путь (синяя синусоида) голубого основания. Эти синусоиды показывают, что среднее ускорение и средняя скорость равны нулю, а пройденный путь колеблется вокруг некой величины. И тоже равен нулю.
Рекомендую обратить внимание, что график скорости смещён на 90 градусов относительно графика ускорения, а график пройденного пути смещён относительно графика ускорения на 180 градусов (cos(a), sin (a), – cos(a)). Так и должно быть, так как скорость – это интеграл от ускорения, а пройденный путь – интеграл от скорости.
Как инерцоид данная модель функционировать не может. Но такие конструкции могут работать в качестве усилителя мощности. На вращение маховиков и дебалансов при хороших подшипниках тратится небольшая энергия, а вот колеблющую голубую платформу можно заставить выполнять очень большую работу, правильно подобрав массы платформы, маховиков и дебалансов, а также угловую скорость вращающих маховики моторы. Чем выше мы установим (в некоторых пределах) радиус маховика, массу дебалансов и частоту вращения моторов, тем больше мощности можем снять с такого устройства. Как это сделать – это уже другой вопрос.
Велко Милкович давно работает с такими системами. Только в качестве сердца своих систем он использует в основном маятники, а не маховики с дебалансами. И когда использует параметрические маятники, то получает, по сути, вечные двигатели, точнее, сверхъединичные устройства.
Пусть инженеры и главные учёные думают. К сожалению, они в этом направлении сильно не дорабатывают. Похоже, им начальство или базовые инвесторы запрещает «копать» в данном направлении. Но мы давно знаем, что такие конструкции могут быть использованы в качестве сердца БТГ большой мощности.
Модель вторая.
На данной модели проверялась идея использовать разную угловую скорость для дебалансов, чтобы получить большую центробежную силу правее осей маховиков, в надежде, что это позволит получить тягу слева направо. Но результат оказался неожиданным. На рис.2. показан результат моделирования.

Рис.2.
Чтобы регулировать частоту вращения моторов в зависимости от положения зелёных дебалансов, внесены изменения в свойства моторов. Для верхнего мотора формула, определяющая его угловую скорость вращения, выглядит так:
if(Body[10].v.y<0, 1, 3)
Для нижнего мотора формула выглядит так:
if(Body[11].v.y>0, -1, -3)
Результат моделирования оказался неожиданным. Несмотря на разную угловую скорость дебалансов справа и слева от оси вращения моторов и маховиков, итоговое перемещение голубого основания за период оказалось равно нулю. Это указывает на то, что за счёт изменения угловой скорости вращения дебалансов не всегда можно получить ожидаемую тягу.
Не получился из модели №2 инерцоид. Это проявится также при моделировании инерцоида Толчина. Но об этом ниже.
Модель третья.
В данной модели инерцоида проверялась возможность получить тягу, изменяя массу дебаланса во время его вращения. Предполагалось, что когда дебаланс будет находиться правее оси мотора, то его масса будет равна 20 кг, а когда слева – то 0.1 кг.

Рис.3.
Остальные параметры: масса платформы 100 кг, угловая скорость вращения моторов и алых маховиков 1 рад/с. Верхний маховик вращается против часовой стрелки, а нижний по часовой стрелке.
Индикатор чётко показывает наличие пульсирующей тяги, как и должно быть в подобной конструкции. Среднее ускорение положительное, поэтому скорость платформы (красный график) возрастает линейно-пульсирующе, а пройденный путь (синий график) возрастает практически пропорционально квадрату времени.
Такой инерцоид можно устанавливать на транспортные средства. Возможно, пассажиров будет немного трясти, но думаю, что они это практически не заметят, если масса транспортного средства будет составлять несколько тонн.
Как управлять массой дебаланса? Думаю, что найдётся несколько способов. Можно в дебалансе держать воду и в нужные моменты переливать её в центр алого маховика. Только делать это следует быстро. Но технически этому нет никаких препятствий.
Модель с небольшим недостатком – тяга пульсирует. Поэтому следует в следующей модели от неё избавиться. Или уменьшить эту пульсацию.
Модель №4.
В данной модели вместо двух дебалансов используется четыре. По два на каждый моховик. Когда одни дебалансы перемещаются справа от осей маховиков, увеличение их массы, а когда дебалансы перемещается слева от осей маховиков (моторов), то массы их уменьшаются. Благодаря чему можно конструктивно проблему перемещения массы из одного дебаланса в другой решить более простыми способами. Получилась вот такая картина

Рис.4.
Болотным цветом изображён возможный БТГ для питания моторов и систем управления. Похоже, алгоритм работы такого инерцоида напоминает алгоритм А.Бережного. Но есть нюансы.
Прекрасно видно, что тяга стала пульсировать с двойной частотой. Минимальное ускорение равно условно 0. Максимальное ускорение равно 1. Нет интервалов с отсутствием тяги. В результате скорость и пройденный путь стали более равномерными. Это показывает, что подобные инерцоиды позволяют создать для пассажиров транспорта более комфортные условия.
Модель №5.
В данной модели вместо двух маховиков с моторами решено «поставить» четыре маховика. Но дебалансы в них повернуть на 90 градусов, чтобы вместо тяги по формуле T=Fц(abs(sin(wt))), получалась тяга по формуле T=Fц(abs(sin(wt))+abs(cos(wt))). Получилась вот такая конструкция.

Рис.5.
График ускорения (зелёный) стал более гладкий. Минимальное ускорение равно условно 1.0. Максимальное ускорение равно 1,41. Тяга, получается, строго положительная. График скорости (красный) стал практически гладкий. Пройденный путь (синий), как и положено ему, стал тоже более гладким. Замечательный получился инерцоид.
Болотный круг в центре – это источник энергии для питания систем инерцоида. Это может быть БТГ, а может быть и обычный ДВС.
В предыдущих статьях, посвящённых моделированию инерцоидов, мной предлагалось использовать инерцоиды, тяга которых вдоль оси Х меняется по закону sin(wt)2 и cos(wt)2. Два таких инерцоида позволяли получить идеальную постоянную тягу. Так как (sin(wt)2+cos(wt)2)=1. Будет хорошо, когда в будущем появится возможность выбора между разными типами инерцоидов.
Модель №6.
Модель Толчина №1.
Предыдущие пять моделей инерцоидов показали, что тягу этим устройствам создают центробежные силы. Между тем сам Толчин в своём описании разработанного им инерцоида писал, что центробежные силы в его устройстве не играют никакой роли. Что дело в продольных силах инерции. Точно также Г.И.Шипов тоже настаивает, что инерцоид Толчина перемещается в пространстве под действием продольных сил инерции. Видимо, поэтому он даже не рассматривает в своём математическом анализе инерцоида Толчина центробежные силы.
В своих предыдущих статьях, в которых постарался проанализировать поведение разных инерцоидов, я обратил внимание, что практически точное следование рекомендациям Толчина, не позволяло мне получать графики ускорения скорости и пройденного пути, которые получались у других моделей. Например, все центробежные модели инерцоидов сразу или через 1-2 цикла выходили на стабильную работу. Ускорение было пульсирующим и повторяющимся от цикла к циклу. Так как среднее значение ускорения было положительным, то скорость инерцоида возрастала линейно с небольшими пульсациями, а пройденный путь стремился возрастать по параболе, которая слегка пульсировала.
Поэтому когда мои модели инерцоида Толчина стали показывать интересные кривые, то понял, что что-то здесь не так. В некоторых моделях ускорение росло вместе со скоростью по амплитуде, но пройденный путь возрастал незначительно, а в некоторых случаях пройденный путь показывал твёрдый ноль. Поэтому я решил разобраться с этим феноменом и создал модель инерцоида Толчина №1.
В этой модели я предположил, что в пределах -30-+30 градусов груз разгоняется мотором, а в пределах 150-210 градусов груз тормозится специальным тормозом так, чтобы после прохождения этой области у груза оставалась энергия, чтобы «дойти» до области разгона.
Получилась примерно такая картинка:

Рис.6.
На этом рисунке прекрасно видно, что инерцоид долго раскачивается. Но затем у него ускорение и скорость начинают сильно колебаться вокруг нуля. В результате пройденный путь за десяток колебаний практически равен нулю. То есть, получился сильно нелинейный вибратор.
Для верхнего маховика с дебалансом в моторе пришлось вводить формулу:
if(abs(sin(body[2].p.r))>0.5, 0, if(cos(body[2].p.r)>0,1,-0.35))
А для нижнего маховика в моторе пришлось вводить формулу:
if(abs(sin(body[3].p.r))>0.5, 0, if(cos(body[3].p.r)>0,-1,0.35))
Возьмём верхнюю формулу. В ней записано, что если дебаланс находится вне зоны разгона, то маховик движется без ускорения. Если сосинус угла поворота маховика больше нуля, то это зона разгона, поэтому угловое ускорение мотора равно 1. Если же косинус угла поворота меньше нуля, то дебаланс находится в зоне торможения. И поэтому он тормозится, угловое ускорение равно -0,35. Так как второй мотор и маховик вращаются в другую сторону, то цифры в свойствах мотора изменены на противоположные.
Вот так это выглядит в программе для верхнего мотора:

Рис.7.
Пока в моей модели предполагается, что ускорение вращения в моторах одинаковое от цикла к циклу. Между тем, сам Толчин в своей книге про инерцоид писал, что его устройство очень капризное. Особенно, когда используется часовая пружина. В начальном периоде пружина имеет высокую мощность. Поэтому ему приходилось несколько первых циклов пропускать вхолостую, давая пружине немного ослабнуть. И тогда он запускал инерцоид в работу, развлекая ими свою публику. Но в конце опыта пружина ослабевала настолько, что её силы уже не хватало для преодоления тормоза. И инерцоид останавливался.
В моей же виртуальной модели «сила пружины» в зоне разгона была постоянной от цикла к циклу, я пока не знаю, как встроить в модель блок, отражающий снижение разгоняющей силы. Но в таком случае мы должны понимать, что модель будет функционировать только некоторое время и обязательно дебалансы прекратят вращаться. Придётся инерцоид «взводить», как это делается в игрушечных машинках. А это уже указывает на то, что инерцоид Толчина, точнее данная моя модель, не годится в качестве движителя для транспортных средств.
Видимо, поэтому некоторые инженеры и учёные отрицательно отзывались и отзываются о инерцоиде Толчина. Ибо не могут понять секрета этого движителя.
Модель №7.
Модель Толчина №2.
Поиграв с моделью инерцоида Толчина №1, я долго думал над тем, почему эта модель инерцоида не показывала ожидаемое поведение. Вроде бы создал участок разгона и участок торможения. Торможение было слабее разгона раза в 3. Но между тем получился вибратор. Если торможение было значительным, больше 0.5, но меньше 1.0, то происходила остановка дебалансов в зоне торможения. Капризная штука получилась.
И тогда пришла мысль, что Толчин не раскрыл нам все свои секреты. Или что-то в его инерцоиде происходило не так, как он предполагал. Учитывая опыт создания других моделей инерцоидов, я предположил, что когда груз находился впереди, то прут, на котором он крепился, слегка удлинялся. Это приводило к увеличению момента инерции груза и увеличению центробежной силы. Но когда груз оказывался сзади, то прут с грузом слегка укорачивался, уменьшался момент инерции и центробежная сила. Разность центробежных сил спереди и сзади инерцоида позволяла ему перемещаться в пространстве за счёт сил инерции.
Но так как мощность часовой пружины постепенно уменьшалась, то инерцоид Толчина мог совершить не более 10 циклов (оборотов грузов).
Если говорить проще, то у инерцоида Толчина, возможно, изменялся момент инерции, что позволяло получать необходимую тягу и перемещение. Возможно, в инерцоиде был и другой секрет. В частности, Толчин в своей книге пишет, что тормоз в инерцоиде выполняет двойное назначение. Он вначале заметно тормозит вращение грузов, а потом «бросает» грузы по кругу в зону разгона. То есть получается, что и зона торможения в его инерцоиде функционирует как сложная система, которую просто так сразу не запрограммируешь. Пока моих способностей как программиста недостаточно для решения этой задачи. Поэтому при программировании данного блока придётся вводить функцию, зависимую от времени, что пока для меня проблематично. Выход, скорее всего, я найду. Вопрос во времени.
Так как создавать новую модель, в которой можно было изменять длину прута, мне было лень, то я решил доработать модель инерцоида Толчина №1. Но вместо изменения длины прута я решил изменять массу дебаланса.
Для учета разгона и торможения для мотора был выбран режим ускорение угловой частоты, а для всей окружности использовались следующие формулы.
Для верхнего маховика с дебалансом в моторе пришлось ставить формулу:
if(abs(sin(body[2].p.r))>0.5, 0, if(cos(body[2].p.r)>0,1,-0.35))
А для нижнего маховика в моторе пришлось вводить формулу:
if(abs(sin(body[3].p.r))>0.5, 0, if(cos(body[3].p.r)>0,-1,0.35))
А для массы красных маховиков пришлось ввести формулы:
Для верхнего дебаланса:
if(abs(sin(body[2].p.r))>0.5, 20, if(cos(body[2].p.r)>0,23,15))
И для нижнего дебаланса:
if(abs(sin(body[3].p.r))>0.5, 20, if(cos(body[3].p.r)>0,23,15))
Таким образом, вне зон разгона и торможения масса грузов была 20 кг, в зоне разгона масса грузов 23 кг, а в зоне торможения масса грузов 15 кг.
Дополнительно пришлось повернуть маховики с дебалансами примерно на 30 градусов для того, чтобы, находясь спереди мотора, каждый дебаланс, пройдя в зоне разгона 60 градусов смог набрать достаточную скорость для преодоления 60 градусов в зоне торможения.
Модель и результат её работы показан на рис.7.

Рис.8.
И хотя результат данного моделирования меня полностью не удовлетворил, но я получил доказательство, что при принятых в данной модели инерцоида Толчина №2 постулатах, некоторые признаки инерцоида появились. Ускорение размашисто наращивала амплитуду вокруг нуля, скорость постепенно нарастала, хотя амплитуда колебаний скорости была очень высокой. Стабильно возрастал пройденный путь примерно по параболе.
Правда, взрывное поведение ускорения указывало на наличие сильной положительной обратной связи. Такое устройство в реальности может просто взорваться или развалиться от собственных вибраций. Флаттер нам не к чему.
Несмотря на то, что данная модель показала некоторые признаки жизни, меня она полностью не удовлетворила. Первое, мне не нравится возрастающая амплитуда, как для ускорения, так и для скорости. Если что и возить на такой платформе, то только мешки с картошкой. Для перевозки людей такой инерцоид не годится.
Можно признать, что используя разные ухищрения, данный плохо управляемый вибратор можно использовать в специально разработанных конструкциях. Раз есть высокие значения ускорения, то такая система годится для создания электровиброгенераторов. Учитывая наличие сильной положительной обратной связи, над таким вибратором придётся потрудиться, чтобы иметь возможность этим ускорением эффективно управлять.
Если есть механическое устройство, то должен быть вариант его моделирования в программе «Живая физика». Но…
Если для управления такого инерцоида требуется компьютер со специальной программой, то тогда мне не понятно, как в таком случае отделить свойства самого инерцоида от того, что добавит ему компьютерная программа. При наличии подходящего программного обеспечения можно спокойно создавать виртуальную модель инерцоида хоть лет двадцать, бесполезно потратив время и деньги. Но можно получить и шедевр инженерной мысли.
Хотя, лично я, предпочёл бы такую конструкцию для инерцоида, в которой можно с самого начала заложить в качестве источника тяги центробежную силу. Например, можно использовать вот такой центробежный инерцоид, у которого будет большая сила и мощность.

Рис.9.
В подобной конструкции можно установить не только 4, но большее число роликов. Это будет зависеть от диаметра инерцоида и запланированной мощности и тяги. Чем больше роликов и угловая скорость вращения вала, тем мощнее и сильнее будут инерцоид.
Можно задействовать и такую тяговую конструкцию, которую в начале нулевых предложил один из участников форума offtop/energy FEMA. Этот человек помогал в 90-е годы перебраться в США Гринкевичу с его группой, автору энергетического бублика.

Рис.10.
В варианте, который предложил FEMA, вместо роликов использовались шарики. Но на конечный результат это не повлияет.
Реальный центробежный движитель, собрал Берсенёв. Двигатель похож на изображённый на рис.10. Хотя у Берсенёва используются шарики, а на рис.10 ролики. Это двойной центробежный инерцоид, хотя Берсенёв божится, что его движитель инерцоидом не является. Но это его дело. У каждого должно быть своё понимание природы используемого им движителя. Вон Владимир Леонов называет свой движитель двигателе. И особо не страдает. Ждёт своего часа, когда правительство и РАН признают за ним научный приоритет как создателя квантонного двигателя. Хотя принцип работы его двигателя имеется в школьном учебнике физики. А примерно в одно время с Леоновым свой аналогичный движитель, слегка иной конструкции предложил Г.Иванов. У обоих получился электромагнитный инерцоид, только из-за высокой частоты формирования электромагнитных импульсов тяги тяга этих инерцоидов воспринимается постоянной.

Рис.11

Рис12.
На рис.11 и рис.12. показано устройство данного движителя. Это, по сути, игрушечный автомобиль с инерцоидным движителем. Хорошо видно, что это центробежный инерцоид, в котором два ухвата гоняют по кругу со смещённой осью вращения два шарика. В принципе легко сделать ухват на 4 шарика, что позволит увеличить тягу у данного движителя в два раза. Но ничего не мешает использовать круглую пластинку с множеством ухватов. Это ещё больше увеличит силу тяги.
Движители вращаются небольшим электрическим моторчиком. На рис.11 он виден как одиноко стоящий цилиндр.
Формула расчёта тяги для варианта Берсенёва выглядит так: F=2m*dR*w2, где m – одного дебаланса, dR – смещение оси вращения ухвата с шариками (шарами), w – угловая скорость вращения ухвата с шариками (шарами).
Произведём расчёт для случая, когда масса шара равна 1 кг, частота вращения 3000 об/мин. А смещение оси вращения составляет 0,1 м. Получаем F = 0,2*(2*3.14*5002, или F=1973920 н, или 197392 кг кг, 197,4 тонн. Если мы снизим обороты вала двигателя до 1000 об/мин, то получим тягу в 22 тонны. Два таких инерцоида поднимут 44 тонны, а 4 – 88 тонн. Возможно, это не так много, но выводить большие грузы на орбиту Земли такое устройство может, да и можно с их помощью собрать летающий автомобиль.
Человек (Берсенёв) собрал действующую модель инерционного (эфирного, безопорного) движителя. Который можно поставить в любой танк, превратив его в летающий. Конечно, он не специалист по тензорному анализу, чтобы придать своему автомобилю и движителю научное обоснование. Наивно писал письма Президенту РФ и в МО РФ. Ценный образец из нашего будущего оказался никому не нужным. Берсенёв рассчитал возможную тягу движителя, который может вращаться любым мотором в 20-30 кватт. Никому такое чудо не нужно. Вот и я иногда думаю, кому нужны эти инерцоиды?
Модель №8.
В модели №6, в которой я попытку смоделировать инерцоид Толчина, мне не понравился резкий рост ускорения и скорости. С другой стороны, пройденный путь практически не возрастал, как это, по идее, должно быть у нормального инерцоида.
Решил по русской привычке, что и так сойдёт, но потом сообразил дать себе несколько дней «на подумать». Вдруг в голову нормальная мысль залетит. И такая мысль залетела.
Я обратил внимание, что даже при наличии зоны разгона и зоны торможения, моя модель Толчина №7 работала как мощный вибратор. И сколько я не пытался подправить уменьшить или увеличить эти зоны, одновременно и порознь, ничего нового у меня не получалось. И тогда всплыла мысль, а не играет ли тормоз в инерцоиде Толчина двойную функцию. С одной стороны это нечто похожее на тормоз, а с другой стороны очень важный элемент инерцоида, создающий в нужном месте и в нужное время тот важный импульс центробежной силы, который как раз и заставлял инерцоид совершить должный шаг по ходу движения. Это еще и своеобразная небольшая катапульта.
Во-первых, тормоз имеет подходящую для этого форму. К нему крепится пружина, которая может перебросить тормоз из одного положения в другой. А как мы знаем, центробежная сила сильно зависит от скорости перемещения тела вдоль окружности. Формула для её вычисления выглядит вот так: Fц=mv2/R. Если у тела будет заметная масса и большая угловая скорость (высокая скорость вдоль окружности), то центробежная сила может оказаться очень большой, хотя для наблюдателя процесс произойдёт очень быстро и он даже не успеет понять, что случилось.
Вначале я поясню, что показало моделирование. Синее основание. Масса неважно. Моторы вращают красные диски с зелёными дебалансами. Частота вращения вала моторов 1 рад/с. Один диск вращается по часовой стрелке, а второй против часовой. Не введи я дополнительные силы, получилась бы модель вибратора. Но получилось небольшое чудо, которое подтвердило мои соображения о роли тормоза.
На верхней части рисунка сила практически не видна. Можно различить небольшую точку. Но когда зеленый дебаланс перейдет на левую сторону красного круга, то стрелка силы станет равна 20 н, а её длина очень большой. Силы в 20 н оказалось достаточно для нейтрализации силы инерции зелёного дебаланса. И получился замечательный результат. Такой же, как и в модели, где я добивался резкого уменьшения центробежной силы с помощью изменения массы дебаланса в модели №3.
Теперь уже не надо думать, куда загонять «лишнюю» массу. Что касается источника силы, то можно установить на зелёный дебаланс инерцоид, создающий постоянную тягу в выбранном направлении (вдоль радиуса у центру дебаланса). И, естественно, потребуется система управления, которая бы включала данный инерцоид в нужный момент и нужном месте.

Рис.13.
На нижней части рис.13 получилась классическая картина. Ускорение (зелёная линия) пульсирует, оставаясь одинаковой от цикла к циклу. Скорость (красная линия) пульсирует и линейно возрастает. А вот пройденный путь (синяя кривая) возрастает по параболе, как и должно быть по классической механике. И главное, никакого вибратора.
На мысль о важной роли тормоза меня подтолкнул просмотр рисунка в одной старой статье о механизме создания центробежных сил. Ещё в 20-х годах прошлого века многие изобретатели пытались придумать инерцоиды, только называли они их по-другому. Вот один пример.
Устьянцев Леонид Степанович предложил свой центробежный движитель. И, похоже, его конструкция не менее простая, а создаваемая движителем центробежная сила даже больше, чем в конструкции Коминова (у Коминова вариант получился плохим). Принцип работы движителя Устьянцева можно уяснить из рисунка, взятого из его патента (рис.14).

Рис.14. Схема центробежного движителя Устьянцева Л.С.
В этой схеме коленвал заставляет вибрировать грузы Г, укрепленные на концах рычагов. Так при вибрации грузы Г перемещаются по части окружности, то при этом создается центробежная сила, которая направлена в сторону, показанной стрелкой с F на конце.
Попытка в программе «Живая физика» вращать с помощью мотора красные маховики с дебалансами попеременно по часовой и против часовой стрелки с использованием режима «Угол поворота» показало, что силы инерции вдоль оси Х возникают, и очень значительные. Но они не приводят к поступательному перемещению инерцоида, как в других случаях моделирования. И инерцоид ведёт себя как нелинейный вибратор.
Возможно, так и должно быть, ибо резкие остановки грузов с последующим изменением направления движения по дуге окружности в движителе Устьянцева Л.С. действительно создают заметные продольные силы инерции, как по оси Y, так и по оси X. И на их фоне центробежная сила получалась относительно незначительной.
Но вначале, до проверки, грузы Г на рис.14. напомнили мне тормоз в инерцоиде Толчина. Поэтому я и решил проверить эту идею пока в тестовом режиме. И сразу вибратор превратился в замечательный, почти идеальный, инерцоид.
Вот тормоз в инерцоиде Толчина.

Рис.15
Получается интересная картина. Толчин выбрал экономный способ расхода энергии часовых пружин. Поэтому он создал участок разгона в передней части инерцоида. Так как масса грузов (дебалансов) была большая, то потери на трение были относительно небольшие. Но когда грузы подходили к противоположному концу инерцоида, то они отодвигали специальную планку и одновременно с помощью планки натягивали пружину. Это внешне смотрелось как торможение грузов. Наверное, так оно и было. Но когда грузы проходили «заднюю» точку траектории, то пружина резко сжималась, по инерции тормозной кулачок резко поворачивался вокруг своей оси. Одновременно планка подталкивала грузы, и они благополучно перемещались в начало инерцоида, где их снова немного подгонял мотор или часовые пружины.
Получалось, что зоне торможения дебаланс вначале резко останавливался, а затем также резко отбрасывался к началу инерцоида. Получалась цепочка из двух резких изменений скорости дебаланса. Центробежная сила обнулялась, в дело вступала продольная инерция, вначале резкое ускорение, а затем резкое ускорение.
Возможно, я ошибаюсь о роли тормозного кулачка в работе инерцоида Толчина. Но модель №8 показывает, что у инерцоида Толчина при достижении грузов области «торможения» появляется некая сила, которая нивелирует центробежные силы от вращающихся грузов. Кроме тормозного кулачка её создать не могут другие части инерцоида. В инерцоиде Торнсона также основную тягу создает невзрачный на вид элемент, который управляется специальным электромагнитом.
Но после проведения моделирования другого варанта инерцоида, результаты которого я не стал включать в данную статью, у меня появилось подозрение, что резкая остановка, а затем отбрасывание грузов тормозом, порождает формирование продольных сил инерции. Как в автобусе с плохим водителем. Одновременно центробежная сила пропадает, что и приводит к нормальной работе инерцоида Толчина.
Модель №9.
В этой модели я попытаюсь, используя дополнительные силы в нужном месте и в нужное время, получить модель инерцоида близкую по своим параметрам с инерцоидом Толчина. Надеюсь, что данная модель будет походить на нормальный инерцоид.
За основу будет взята модель №9, только компенсация центробежной силы будет происходить в пределах 150-210 градусов. Этим самым только центробежные силы, создаваемые в пределах -30-+30 градусов будут создавать тягу, а остальные силы будут попарно друг друга уничтожать.
Получился вот такая модель и такой результат:

Рис.16.
В данной модели для силы применена такая программка
if (cos(body[2].p.r)<=0.866,-20,-0.1)
В результате при запуске программы выяснилось, что силы блокируют центробежную силу от зелёных дебалансов почти в пределах 300 градусов. А в зоне разгона центробежная сила не блокировалась. Получились графики на рис.16.
Дальнейшее усложнение программы для управления силами проводить не стал, так как модель решает поставленную перед ней задачу. Она не блокирует центробежную силу в зоне разгона, но блокирует центробежную силу в зоне торможения. Попутно она блокирует центробежную силу и по остальным углам. Но даже, если бы я доработал условия для работы сил до конца, на окончательный результат это уже не повлияло, так как остальные участки окружности, сверху и снизу, на перемещение инерцоида уже не влияли. Поэтому я решил остановиться на достигнутом результате.
По графикам видно, что инерцоид создаёт всплески тяги, которые придают голубому основанию большое ускорение (зелёный график), скорость растёт ступенчато, возрастая от цикла к циклу (красный график), а пройденный путь представляет практически правильную параболу (синий график).
Чтобы такой инерцоид можно было поставить на транспортное средство, в него следует ввести трение, которое после нескольких циклов могло бы противопоставить себя среднему ускорению, стабилизировать скорость вдоль оси Х и вместо роста пройденного пути по параболе получить для пройденного пути линейную зависимость от времени. При незначительном трении проблему неравномерности перемещения можно решать временной остановкой инерцоида и движением по инерции, согласно первому закону Ньютона.
В качестве устройства, блокирующего центробежную силу, можно использовать инерцоиды, создающие пульсирующую или постоянную тягу. Но можно придумать что-то похожее на недоделанный электрический мотор. Или подсмотреть у Торнсона, правильно подобрав направление выброса его пластинки.
Попытка создать модель Толчина, в которой использовались бы колебания грузов в узком диапазоне углов, провалилась. Удалось в свойствах мотора найти опцию «Угол поворота». При этой опции программа «заставляла» колебаться дебаланс в пределах радиана по часовой и против часовой стрелки. На индикаторе фиксировались некие синусоподобные кривые, иногда сильно деформированные, для ускорения, скорости и пройденного пути. В среднем получались нули. Видимо, программа показывала формирование продольных сил инерции, на фоне которых центробежные силы терялись и инерцоид превращался в вибратор. Похоже, нужны эксперименты в более точной программе, либо проведение натурных испытаний. Но для последних у меня возможности нет.
Модель №10.
После модели №9 думал заканчивать временно с моделированием инерцоидов, тем более, создать модель инерцоида Толчина оказалось не так просто. У инерцоида Толчина оказался секрет, к разгадке которого я подошёл, но как практически решить эту проблему, мысль нужная никак не приходила.
В голове вертелась идея, что тормоз с пружиной Толчин ввёл в свой инерцоид не просто так. Возникло подозрение, что в инерцоиде Толчин сумел вместо центробежной силы использовать продольную инерцию. Но эта идея противоречила моим представлениям, тем более я знал, что продольная инерция в классическом исполнении не позволяет создать инерцоид. Всё это было мной проверено в моделях ещё в 2019 году.
Но тут решил для создания продольной инерции использовать новый подход. Суть в следующем. Ударник с большой массой располагается на маховике на оси. С помощью внешней силы ударник поворачивается вместе с маховиком с нулевого угла до почти 180 градусов, совершая при этом полуоборот. А там ударник ударяет о цилиндр, упор, закреплённый на основании. Предполагаем, что упругости материалов ударника и упора в виде цилиндра равны 1.0 (абсолютная упругость).
Упругий ударник ударяет по упругому цилиндру на основании и толкает основание. Сам ударник после удара возвращается на начальную позицию. Но не по прямой, а по полуокружности.
Всё это время ударник находится под действием силы, как при движении вперёд, так и при движении назад под воздействием силы инерции.
Получилась простая модель:

Рис.17.
Специально создал рисунок, чтобы показать, как перемещается во время работы инерцоида ударники (сини кружки).

Рис.18.
Эти траектории показаны белыми полуокружностями. Синие ударники под действием сил, показанных в виде стрелок, вначале двигаются к красным упорам, жестко закреплённых на зелёной платформе по полуокружности, затем сильно бьют по красным упорам, платформа получает ускорение справа налево, а синие ударники откатываются назад в исходному положению, чтобы после короткой остановки вновь начать движение к красным упорам. И так регулярно бьют по упорам, что ведёт к увеличению скорости платформы и наращиванию пройденного пути.
По сути, для меня это было открытием, доказывающим, что продольные силы можно использовать в инерцоиде.
Полученные графики для ускорения, скорости и пройденного пути для платформы меня поразили. Только платформа поехала не слева направо, а справа налево, в ту сторону, куда её «гнал» синий ударник. А последний двигался по кругу вместе с оранжевым маховиком под действием постоянно действующей силы.
Кривая ускорения зелёного цвета получилась сложной формы, но тяга оказалась направленной справа налево. Красная кривая для скорости платформы вела себя, как и положено хорошему инерцоиду, увеличивалась волнисто-линейно. А пройденный путь (синяя кривая) возрастал по кривой, близкой к параболе. Естественно, графики скорости и пройденного пути показывали перемещение справа налево.
Сразу после моделирования решил модель доработать, чтобы ударник вращался попеременно по часовой и против часовой стрелки. Но потом подумал, что ничего нового я получить из этой схемы не смогу. Частота ударов ударника о красный упор осталась бы прежней, сила инерции вдоль оси Х также не изменилась бы.
Хотя технически в натуре реализовать эту идею можно. Хотя бы для равномерного износа ударника и упора. Главное, что этот инерцоид имеет простое устройство, и показывает замечательные, даже неожиданные результаты.
С другой стороны эта модель инерцоида проясняет саму идею инерцоида Толчина – в зоне 180 градусов груз (дебаланс) останавливается упругим упором, а затем отбрасывается силой инерции в начальное положение. Правда, не по старой траектории, а продолжая свой путь по окружности.
Проверил я, как влияет упругость дебаланса и упора на ход процессов. Оказалось, что уменьшение коэффициента упругости с 1.0 до 0.8 через несколько циклов останавливают колебания дебалансов, Они начинают давить на упоры и мы получаем некий транспорт, который движется вперёд (назад) под действием постоянных сил. В качестве которых могут выступать любые безопорные силы, например, созданные другими инерцоидами.
Как быть дальше?
Рассмотрим ещё раз графики для ускорения, скорости и пройденного пути, полученные при моделировании модели №10.
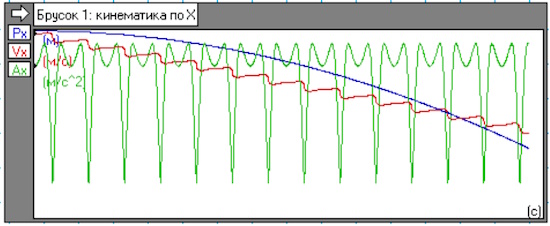
Рис.19.
Сравним эти графики с графиками, на рисунке (Рис.20) из книги, посвящённой инерцоиду Г.И.Шипова. К этому графику у меня несколько вопросов, так как некоторые мелочи на данном рисунке заставляют меня насторожиться.
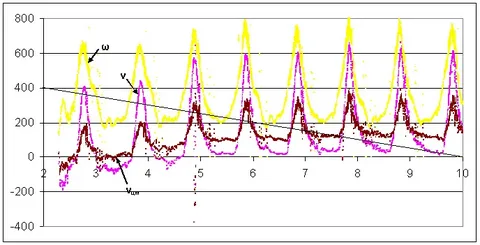
Рис.20.
Во-первых, скорость у инерцоида, как правило, должна возрастать ступенчато, хотя амплитуда колебаний скорости может достигать большой величины. В данном случае, средняя скорость практически не возрастает. А раз скорость не меняется, то нет ускорения и соответственно нет силы, которая могла бы вызвать это ускорение.
В-вторых, на графике нет кривой ускорения и пройденного пути. Либо в данных опытах ускорение и пройденный путь не измерялись, либо по какой-то причине было принято решение ускорение и пройденный путь не фиксировать (не отображать).
Я уже показывал, что переменная угловая частота вращения дебалансов не позволяет получить тягу за счёт ускорения угловой скорости грузов на одном участке траектории и замедления угловой скорости на другом участке траектории. Как-то пройденные пути компенсируются. Это показано во второй модели. Например, сдвиг вправо происходит с высокой скоростью, а сдвиг влево осуществляется с меньшей скоростью. Но в результате платформа возвращается на первоначальное место. И так от одного цикла к следующему. Это показано в модели №2.
Очень бы хотелось получить от Г.И.Шипова ответы на данные вопросы. Мне они необходимы для разработки более совершенных моделей инерцоида Толчина в программе «Живая физика». При условии, что программа позволит это сделать.
Хотелось бы затронуть ещё один момент. Г.И.Шипов и ряд других исследователей часто упоминают инерцоид Торнсона, о котором официальная наука предпочитает молчать. Практически все исследователи в один голос повторяют, что дебалансы в инерцоиде Торнсона двигаются по кривой, которую называют кардиоидой. Мной проведена оценка возможности использования такой кривой в качестве регулятора тяги. Оказалось, что движение груза по такой кривой тяги не создаёт.
Мне пришлось искать в Интернете настоящий патент Торнсона с подробным описанием его технологии и целым рядом чертежей. Выяснилось, что вместо кордиоиды дебаланс совершает более сложную траекторию. Примерно, как изображено на следующем рисунке.

Рис.17. Кардиоида Торнсона.
Груз перемещается не только по кардиоиде, но и совершает замкнутый виток, который как раз и создаёт тягу. На чертежах Торнсона этот виток совершает небольшой груз, которым управляет электромагнит. Когда груз подходит к неподвижному диску, из него выбрасывается электромагнитом небольшой груз, который совершает небольшой завиток, в пределах которого и создаётся тяга в инерцоиде Торнсона.
Таких блоков в инерцоиде Торнсона два, что позволяет получить тягу без лишнего момента вращения.
Аналогичное устройство для получения тяги было мной описано в одной из ранее написанных статей. Один товарищ загадал мне загадку, через год я её разгадал, а он в благодарность дал более подробное описание инерцоида нового типа. В той схеме груз совершает перемещение по окружности, а не по кардиоиде. Вот и вся недолга. Даю вырезку из статьи.
12.05.2013 я получил от Рублёва Анатолия Николаевича письмо с pdf-файлом, в котором содержалась статья Рублёва А.Н. «О центробежном движителе». Эту статью я еще раньше нашел в Интернете, причем страниц в этой статье было не менее 5-6. Недавно решил вновь просканировать Интернет в поиске этой статьи. Нашёл только один адрес. Поэтому решил эту статью разместить у себя на сайте, так как идея, высказанная в статье, заслуживает большого внимания.
Во время переписки с Рублёвым А.Н. мне удалось, как мне кажется, в основном понять суть его идеи и предложить два варианта движителя, которые решил опубликовать в надежде, что кое-кто еще не побрезгует и поломает извилины своего мозга с целью разработки более технологичного варианта центробежного движителя. Сам же Рублёв В.Н почему-то считает, что человечество еще не заслужило узнать, что центробежный движитель в механическом варианте можно собрать их обычных шестеренок с дебалансами.
В принципе, центробежный движитель можно сделать из большого подшипника, если правильно его «приготовить». Подшипник следует посадить на вал. И немного с одной стороны прижать к валу. Тогда шарики и ролики в подшипнике будут двигаться по таким траекториям, где будут создаваться несколько разные центробежные силы. Меньше там, где подшипник будет прижат, и больше там, где прижатия уже не будет. Тяга будет направлена туда, где подшипник будет не прижат. Каждый шарик или ролик будет создавать незначительную центробежную силу, но шариков и роликов много, да и вал можно заставить вращаться с большой угловой скоростью. В итоге получим мощную тягу. Такое предложение давно в Интернете высказал один пенсионер. Он предлагал устанавливать такие инерцоиды на валы передних колёс велосипедов. Тягу он предлагал регулировать величиной давления на обечайку подшипника. Но наша система не смогла переварить такую адскую машину. И поэтому такие велосипеды-самокаты ещё долго не появятся ни в РФ, ни в других странах. Хотя наладить производство таких подшипников проще пареной репы. Ими можно оснастить не только велосипеды, но и мотоциклы с автомобилями. Вначале разгоняемся как обычно, затем жмем на подшипник и добиваемся необходимой тяги, снижая нагрузку на мотор. И даже выключая его.
Вернёмся к предложению Рублёва А.Н. Предположим, у нас есть неподвижная система координат в точке А, подвижная в точке В, от которой отходит рычаг с грузом С на конце. Масса груза С равна М. При этом точка В вращается по окружности радиуса R вокруг точки А, а груз С – вокруг точки В с одинаковой угловой скоростью по окружности 2 с радиусом R. Радиусы окружностей 1 и 2 взяты равными друг другу. В этом случае движение точки С происходит по окружности 3 также с радиусом R. При других соотношения между радиусами окружностей 1 и 2 движение точки С в неподвижной системе координат уже не будет происходить по окружности, но не думаю, что качественно результат будет отличаться от того, что будет получен ниже. Возможно, траектория будет близка к эллипсу. Схематически, это можно изобразить так, как это сделано на рис.15.

Рис.18. Схема одного из моих вариантов центробежного движителя.
На этой схеме точка А – это центр неподвижной системы координат. Точка В вращается вокруг неподвижной точки А с постоянной угловой скоростью w по окружности 1. А точка С вращается вокруг точки В также с постоянной угловой скоростью w по окружности 2, но в другую сторону. Окружность 2 неподвижная относительно точки В, но при этом вращается вокруг точки А. В данном варианте принято, что точка В вращается вокруг точки А по часовой стрелке, а точка С вокруг точки В – против часовой. В результате, точка С будет в неподвижной системе координат, связанной с точкой А, вращаться по окружности 3.
Так как нам надо определить за период (один оборот вокруг точки А) результирующую центробежных сил относительно неподвижной системы координат, связанной с точкой А, то сделать это оказывается легко. Для этого надо будет для любого момента времени рассчитать положение точки С, найти проекцию этой точки на отрезок АВ, ну а далее легко можно вычислить и значение центробежной силы. Останется проинтегрировать эту силу от 0 до 2*пи (6,28) и разделить на 2*пи (6.28).
Центробежная сила для груза С относительно точки А можно вычислить по формуле F=Mw2r=Mw2R(1-cos(a)). Интегрируем эту силу от 0 до 2*пи и делим результат на 2*пи. В результате получаем, что средняя величина центробежной силы равна Fср=Mw2R. И направлена эта сила будет вправо. Но эта сила будет меняться во времени от 0 до 2Mw2R, поэтому, как считает Рублёв А.Н., необходимо минимум 4 таких движителя, грузы которых будут вращаться с последовательным сдвигом в 90o, чтобы тяга была достаточно равномерной. Но и при двух движителях, в которых вращение грузов С будет сдвинуто на 180 градусов, можно получить постоянную слегка пульсирующую тягу.
В инерцоиде Торнсона предлагаемый мной алгоритм вращения груза инерцоида как раз и реализован в виде внутренней траектории в форме эллипса. Эллипс – это тоже окружность, но только сжатая по вертикали или горизонтали.
После неудачи с моделированием одного варианта инерцоида Толчина, который я не стал описывать в данной статье, пришёл к выводу, что схема центробежного движителя Устьянцева Л.С. нуждается в дальнейшем изучении. Надо понять, почему колебания груза в программе «Живая физика» только с охватом небольшого сектора окружности не приводило к формированию центробежной силы. Может быть это связано с тем, что груз, двигаясь туда-сюда, сверху вниз и обратно, разрушал структуру окружающего пространства. Или продольные ускорения разрушали центробежную силу, на которую надеялся Устьянцев Л.С.
В результате условия для создания центробежной силы не формировались. Не исключаю, что в будущем эту проблему удастся решить. При этом надежды на большую науку нет совсем. Не хочет наука изучать силы инерции, как продольные, так и центробежные. Многие академики не признают наличие центробежных сил. А некоторые даже не признают реальность любых сил инерции вообще. Мол, это фейк природы.
После приведённых в статье 10 вариантов моделей инерцоидом, реализованных в программе «Живая физика», вроде бы стало понятно, как можно создать модель инерцоида Толчина. У меня в голове вертятся два варианта, которые могут оказаться близкими к реальности. Но этому мешают некоторые трудности, связанные с программой «Живая физика». Пока я не знаю, как быстро мне удастся их разрешить, но пока займусь более важными делами.
Дело также в том, что на транспортное средство инерцоид Толчина ставить смысла нет. Слишком сложно и ненадёжно. Есть более простые технические решения в виде центробежных инерцоидов или электромагнитных движителей типа двигателя Владимира Леонова, о которых я писал в статье «Танки грязи не боятся». Да и других тоже.
Для центробежных инерцоидов справедлив закон – увеличение угловой скорости вращения в 2 раза приводит к увеличению тяги в 4 раза. Тогда как затраты электроэнергии или бензина навряд ли увеличатся в два раза, ибо вращать маховик на хороших подшипниках не потребует значительной энергии. Так что сделать с такими движителями танк, способный передвигаться по любому болоту, вполне реально. А если повезёт, то можно построить и летающий танк, что позволит ему эффективно бороться с любым летающим дроном. Это будет НЛО с большой пушкой.
Заключение.
В данной статье я создал в программе «Живая физика» 10 моделей инерцоидов. Показаны параметры моделей. Представлен результат их работы. Сделаны должные выводы о возможности использования этих инерцоидов.
Во время этих виртуальных экспериментов в программе «Живая физика» мной совершены несколько открытий.
Одно из них состоит в том, что продольные силы инерции могут разрушать центробежную силу. Вроде бы, очевидная вещь, а проявилась только в результате численного эксперимента. Хотя понятно, что любая остановка при движении тела по окружности моментально ведёт к обнулению центробежной силы.
Второе открытие состоит в том, что найден способ использования продольной инерции для создания инерцоида. Оказалось, что ударник следует перемещать не по прямой, а по окружности. Тем самым, вторая сила заматывается в маховике, а первая сила толкает инерцоид вперёд. Данное открытие нуждается в проверке.
Третье открытие состоит в том, что одну центробежную силу можно уравновесить другой центробежной силой. Или одну безопорную силу уравновесить другой безопорной силой. Это позволит создавать инерцоиды или движители с возможностью создавать тягу в любом направлении, меняя её по ходу перемещения транспортного средства..
Сделана очередная попытка создать модель инерцоида Толчина. Оказалось, что первые две модели инерцоида Толчина трудно поддаются моделированию, модель неустойчива в работе, а в некоторых случаях превращается в обычный нелинейный вибратор. Видимо в эти модели я заложил неправильные условия.
Предпоследние две модели показали неплохие результаты. Модели чётко создают центробежные импульсы в зоне разгона. Скорость нарастает линейно и уступами, а пройденный путь близок к параболе. Эти результаты хорошо согласуются с ранее полученными результатами для других моделей инерцоидов. Для инерцоидов оказалась важной равномерное вращение дебалансов. Только в этом случае возникают настоящие и стабильные центробежные силы. Если груз, двигаясь по окружности, часто и резко меняет скорость и направление движения (вперёд-назад), то появляются мощные продольные силы инерции, типа тех, что возникают у пассажиров автобуса, если последним управляет неопытный шофёр.
Очень интересна модель №10. В которой вращение ударника превращается в силу инерции, заставляющую инерцоид должным образом перемещаться в пространстве вдоль оси Х.
Вполне возможно, для создания более точной модели инерцоида Толчина в программе «Живая физика» мне потребуется новая версия программы и дополнительная информация от читателей. Поэтому я размещаю с некоторых пор адрес своей электронной почты. Иногда даже небольшая подсказка оказывается важнее многих лет поиска не там где темно, а где светлее. А там, где светло, часто всё так затоптано, что правду найти невозможно.
Источники:
Толчин В.Н. Инерциоид. Силы инерции как источник движения. Пермь. 1977.
Власов В.Н. Моделирование инерцоида Толчина.
Власов В.Н. Моделирование инерцоида Толчина 2.
Власов В.Н. Моделирование инерцоида Толчина 3.
Власов В.Н. Танки грязи не боятся.
Власов В.Н. От магнитного мотора до звездолёта.
Власов В.Н. Теория инерцоидов и барабанные инерцоиды в качестве движителя для разных видов транспорта.
Власов В.Н. Что такое инерция?
Власов В.Н. Архив моделей инерцоидов для ЖФ.
Г.И. Шипов Открытие в России поля инерции и сумма торсионных технологий
Г.И. Шипов. Объяснение движения инерцоида Толчина в неголономной механике.
Г.И. Шипов. Проблема инерции как причина застоя в теоретической физике.
В.И. Богомолов. Открытие поля центробежных сил инерции и изобретения устройств для решающих экспериментов.
Текст составлен 13.08.2025.
Безтопливная энергетика
На главную